Chapter 9 Stress Testing, Sensitivity, and Robustness

Chapter Preview. In previous chapters, we explored how to utilize constrained optimization to construct desirable insurable risk portfolios. To recap, building on Display (7.1), many risk retention problems can be formulated as:

\[\begin{equation} \begin{array}{lc} {\small \text{minimize}_{z_0 ,\boldsymbol \theta}} & f_0(z_0, \boldsymbol \theta) \\ {\small \text{subject to}} & ~~~~~RTC(\boldsymbol \theta) \le RTC_{max} \\ & {\bf P} \boldsymbol \theta \le {\bf p}_0 ~~. \end{array} \tag{9.1} \end{equation}\]

Here, the objective function \(f_0(z_0,\boldsymbol \theta)\) represents either a risk measure summarizing the uncertainty of retained risks or a function that, when optimized, yields a risk measure (as developed in Section 7.2). The set of decision variables is denoted as \({\bf z} = (z_0, \boldsymbol \theta)\), consisting of an auxiliary variable and the risk retention coefficients. The constraints include a budget constraint, \(RTC(\boldsymbol \theta) \le RTC_{max}\), as well as linear constraints on the risk retention parameters of the form \({\bf P} \boldsymbol \theta \le {\bf p}_0\). Both the objective function \(f_0\) and the risk transfer cost \(RTC\) can be determined analytically or via simulation.

Analysts find great satisfaction in producing an optimal set of results, knowing they have achieved the best possible outcome within a defined structure. However, like any mathematical representation, constrained optimization results are reliant on model assumptions. Therefore, when interpreting findings, it is natural to question the reliability of the results, something that risk managers are keen to understand. Particularly, one would like to know how the results respond to changes in assumptions.

Stress Testing. How can an analyst quantify these effects? The most direct approach, often termed stress testing, involves allowing a quantity of interest to vary over a range of potential values and observing how the optimization performs over this range. This approach is readily interpretable and requires no new theory. We already have witnessed stress testing in action for the ANU case in Section 8.2. In that section, we examined the reliability of results due to changes in the budget constraint, different choices of the confidence level, and by varying the risk measure. Section 9.1 will further explore this theme by evaluating alternative levels of dependence.

Sensitivity Analysis. Although stress testing is intuitively appealing, it can be time-consuming to rerun optimization procedures across many different plausible scenarios. Hence, Section 9.2 introduces a tool known in economics as the Envelope Theorem, used to calculate local sensitivities. By “local,” we emphasize that the Envelope theorem captures marginal changes assuming small changes in an assumption, i.e., a differential approach, which we refer to as a sensitivity.

Section 9.3 demonstrates how the Envelope theorem can be applied to risk retention problems. As shown in this section, this tool is particularly valuable for understanding the impact on assumptions that solely affect the objective function, such as the choice of the risk measure. The next chapter presents an extension of the Envelope theorem that will allow us to handle more complex alternatives.

Robustness. Sensitivity analysis is limited to measuring the impact of small, or local, changes in assumptions. In the operations research literature, alternative techniques designed to study the impact of larger changes have been developed. Section 9.4 concludes the chapter with a review of different approaches to computing potential variations in optimization results to large changes in assumptions, known as robustness.

9.1 Dependence Stress Testing

As with financial risks, it is widely understood that the dependence among risks is crucial when making decisions to manage them. For instance, if a risk owner is responsible for properties within the same earthquake fault region, a single event like a major earthquake could cause serious losses across many risks. These risks are dependent, highlighting the importance of considering dependency when constructing portfolios. Further applications where dependence may impact a collection of risks will be discussed in Chapter 12. For this section, we assume that dependence is a key aspect of modeling risk portfolios.

Selecting an approach to measure dependence is another important aspect of dependence modeling. While historically prominent methods like multivariate normal distributions and Pearson correlations are familiar to many analysts, they are better suited for risks with thin tails and linear relationships. However, for insurable risks, distributions with heavier tails and non-linear relationships are more common. Copulas, introduced in Section 4.2, are often used to model dependence among multivariate outcomes in risk and insurance. We adopt this approach in this book.

How accurately can one measure dependence? We have already seen the Wisconsin Property Fund example in Section 8.1, where very detailed data allowed for reasonably precise estimation of the dependence model. In contrast, for the ANU case in Section 8.2, many of the risk occurred infrequently. This makes it challenging to calibrate the marginal risk distribution and impossible to accurately estimate dependence. To address these challenges, this section demonstrates how stress testing can be used to calibrate the impact of dependence.

To establish a range of potential dependency models, we begin with a worst-case scenario known as the comonotonic case. You can think of this as a model for a set of properties within the same earthquake fault region. Mathematically, in copula modeling, a widely used restriction is the Fréchet-Höeffding upper bound, given as \[ C(v_1, \ldots, v_p) \le \min(v_1, \ldots, v_p)=C^{upper}(v_1, \ldots, v_p). \] To see this equation, note that for any copula, \[ C(v_1, \ldots, v_p)=\Pr(V_1 \le v_1, \ldots, V_p \le v_p) \le \Pr(V_j \le v_j) = v_j, \] for \(j=1, \ldots, p\). Because the copula is bounded by any argument \(v_j\), it must be bounded by the minimum of all such arguments, which is the Fréchet-Höeffding upper bound. Further, note that this bound is attainable when \(V_1 = \cdots = V_p\). This is the comonotonic case; you can think of these risks as being perfectly positively dependent upon one another. See Denuit et al. (2006), Chapter 2, for a general introduction to comonotonicity.

If there are only two risks, then it is possible to define perfectly negatively dependent risks such as \((V_1,V_2)\) where \(V_2 = 1- V_1\). However, with more than two risks, there is less agreement in the literature on what constitutes perfect negative dependence, cf. Puccetti and Wang (2015). As an alternative, we utilize the case of independence as the lower bound for our range for stress testing. Denote \(C^{ind}(v_1, \ldots, v_p) = v_1 \cdots v_p\) to be the independence copula.

For stress testing, we consider the mixture distribution, defined as \[ C^{w}(v_1, \ldots, v_p) = w~C^{upper}(v_1, \ldots, v_p)+(1-w)~C^{ind}(v_1, \ldots, v_p), \] where \(w\) is a constant, \(0 \le w \le 1\). This distribution is easy to quantify using simulation. To illustrate, see Section 8.3.6 for a description of the ANU data generation process that is based on mixture copulas. By allowing the mixing weight \(w\) to vary, we are able to assess the effects of dependence.

---

Example 9.1.1. Effects of Dependence on Optimal an ANU Risk Portfolio. To exhibit the effects of varying dependence, we return to stress testing of the ANU case described in Section 8.2. As before, To keep the number of comparisons manageable, only results for \(RTC_{max}= 722\) and \(\alpha = 0.80\) are reported.

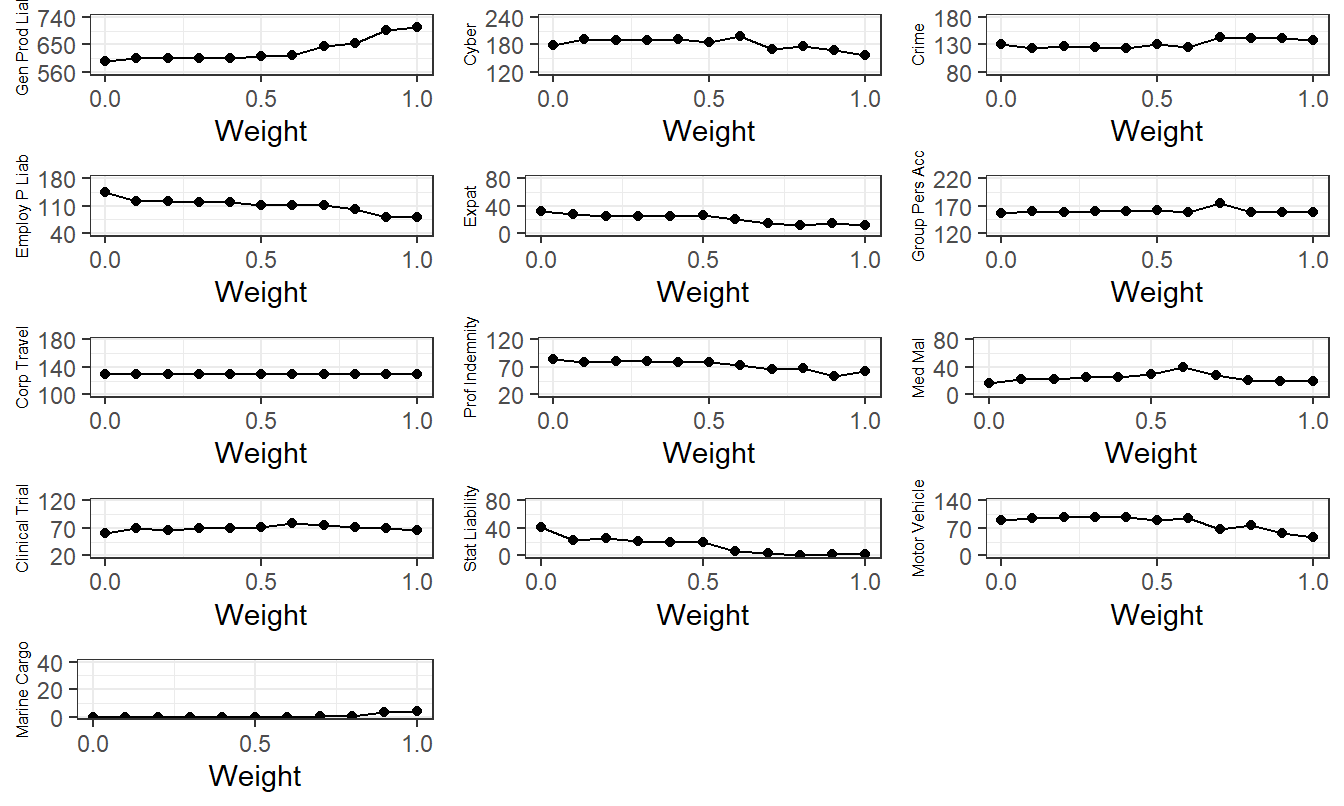
Results are summarized in Table 9.1 and Figures 9.1 and 9.2. In Table 9.1 and Figure 9.1, we see that each of the retained risk measures, \(VaR\), \(ES\), and standard deviation, increases as the dependency increases (that is, as \(w\) increases.)

With Table 9.1 and Figure 9.2, we can get a sense as to how the dependency affects the optimal upper limits. These displays suggest that the optimal limits appear to be relatively stable as one moves from the comonotonic case (\(w=1\)) to the case of independence (\(w=0\)). Such a result would be pleasing to the risk manager, suggesting that the optimal insurable risk portfolios are relatively robust to the dependence assumption.

R Code for Varying Dependency

# Code to Bring in Risk Distribution Parameters

varSelect <- 2:15  # Choose = 2:15 to omit Property
numVars   <- length(varSelect)

#  Bring in Some Data
RiskParameters<- read.csv("Data/ANURiskParameters.csv",header=T)

riskTypes             <- RiskParameters$Class.of.Insurance
riskTypesShort        <- RiskParameters$Class
riskTypesSelect       <- riskTypes[varSelect]
riskTypesShortSelect  <- riskTypesShort[varSelect]

ANU.mu  <- RiskParameters$Premium / 1000  #thousands of AUD
TotCost <- sum(ANU.mu[-1])

RMAggClaims.fct <- function(propCoeff=uPropFixed, AggClaims=Claims, coeff){
  VaR.x     <- coeff[1]
  u.vec     <- c(propCoeff, coeff[-1])  #property is fixed
  LimClaims <- AggClaims
  for (jVar in 1:ncol(LimClaims)){
    LimClaims[,jVar] = pmin(LimClaims[,jVar],u.vec[jVar])
  }
  temp  <- colMeans(AggClaims) - colMeans(LimClaims) 
  RTC.R <- sum(temp[-1])        # do not include property
  AggY  <- rowSums(LimClaims)
  VaR   <- as.numeric(quantile(AggY, prob = alpha))
  CTEmin<- as.numeric(VaR.x + ( mean(pmax(AggY - VaR.x, 0)) )/(1-alpha) )  
  CTE   <- as.numeric(VaR   + ( mean(pmax(AggY - VaR,   0)) )/(1-alpha) ) 
  stddev  <- sd(AggY)
  return(c(RTC.R, VaR, CTEmin, CTE, stddev))
}


# save(ANURTCmax.vec, OutANUProp.ES,
#      file= "../ChapTablesData/Chap8/OutANUProp.ESMar2024.Rdata")
load(file= "../ChapTablesData/Chap8/OutANUProp.ESMar2024.Rdata")
starter.coeff <- OutANUProp.ES[6,c(3,8:21)]
RTCmax        <- ANURTCmax.vec[6]
set.seed(123)
alpha        <- 0.80 
nsim         <- 10000
uPropFixed   <- 5000

f0Depend.ES  <- function(coeff){RMAggClaims.fct(propCoeff=uPropFixed, 
                                                 AggClaims=Claims, coeff)[3]}
RTCDepend.ES <- function(coeff){RMAggClaims.fct(propCoeff=uPropFixed, 
                                                 AggClaims=Claims, coeff)[1]}

time1 <- Sys.time()
readData <- function(wStar,nsim=nsim){
  fileName <- paste("../Data/SimDataMay/AggClaimsMay100Kw",wStar,".Rdata",sep="" )  
  load(file = fileName)
  AggClaims <- Claims[1:nsim,]
  return(AggClaims)
  }

wStar.vec <-  seq(from=0.0, to=1, length.out=11)
RTCmaxFix <- TotCost * 0.5

OutMat.Depend  <- matrix(0,nrow = length(wStar.vec), ncol = 15 + 5)  
u.names <- paste("$u_{",2:(1+14), "}$", sep="")
colnames(OutMat.Depend) <- c("$w$", "LME1" , "$RTC$", "$VaR$", "$ES$", "Std Dev", u.names)

starterDir <- OutANUProp.ES[6,c(3,8:21)] * 0.8


hinDepend.ES <- function(coeff) {h <- NA
    h[1] <- (RTCmax - RTCDepend.ES(coeff))*1e6 
    for (j in 1:numVars){h[j+1] <- 1e6 * coeff[j]} 
    return(h)}

for (jCost in 1:length(wStar.vec)){
  Claims <- readData(wStar = wStar.vec[jCost],nsim=nsim)
  Depend.opt <- alabama::auglag(par=starterDir, 
           fn=f0Depend.ES,                          
           hin=hinDepend.ES,              
           control.outer=list(method="nlminb",trace=FALSE))
  uparams <- Depend.opt$par[-1]
  output <- c(1-wStar.vec[jCost], Depend.opt$lambda[1],
              RMAggClaims.fct(propCoeff=uPropFixed, AggClaims=Claims, 
                              Depend.opt$par)[-c(3)], uparams)
  cat("alabama results",output, "\n")    
  OutMat.Depend[jCost,] <- output
}    

save(OutMat.Depend,
     file= "../ChapTablesData/Chap9/OutMatDepend.Mar2024.Rdata")

Sys.time() - time1 # 5.901147 mins for 10000 nsim

Table 9.1: ANU Excess of Loss Optimization - Varying Dependency

\(w\)	\(RTC\)	\(VaR\)	\(ES\)	Std Dev	\(u_2\)	\(u_3\)	\(u_4\)
1.0	722	5557	6947	2653	440	504	299
0.9	722	5510	6851	2610	392	498	296
0.8	722	5465	6713	2549	320	538	326
0.7	722	5445	6558	2479	256	550	335
0.6	722	5437	6428	2419	313	570	300
0.5	722	5431	6353	2380	349	593	298
0.4	722	5423	6214	2313	355	551	294
0.3	722	5422	6095	2252	337	550	312
0.2	722	5419	5981	2194	350	541	318
0.1	722	5416	5865	2130	286	542	367
0.0	722	5409	5727	2062	377	494	399

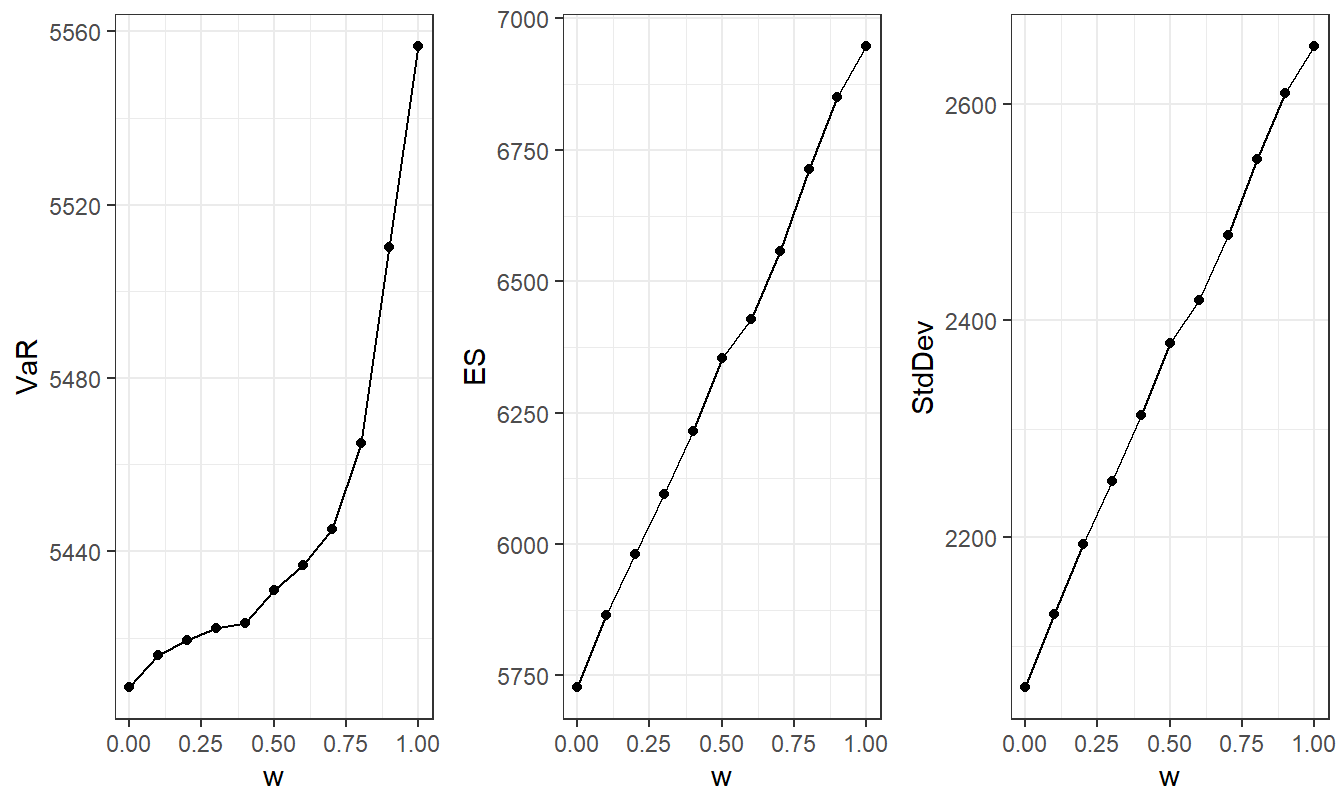
Figure 9.1: Trade-off of Retained Risk versus Dependency Weight. Based on the ANU Excess of Loss Case Study where upper limits are determined by minimizing the \(ES\) criterion.

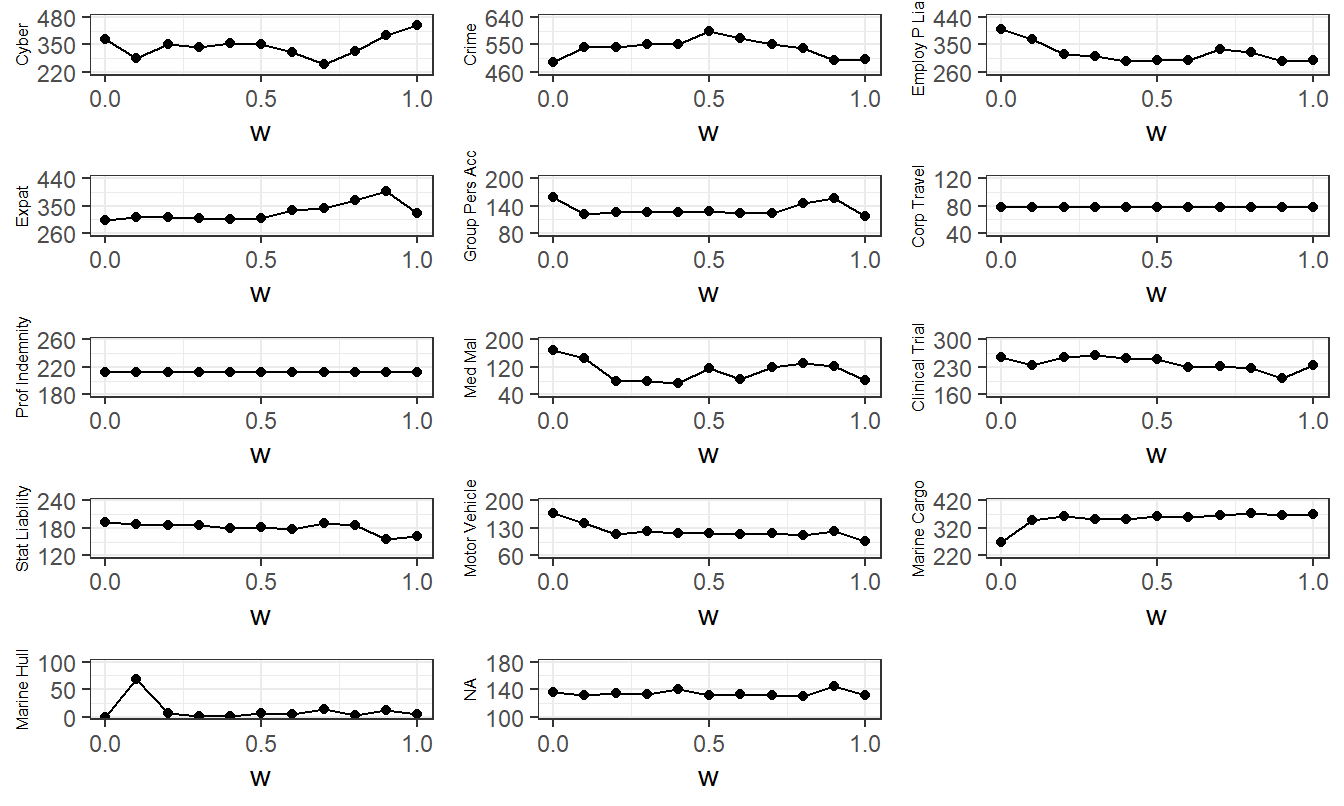
Figure 9.2: Upper Limits versus Mixing Weight. Based on minimizing the \(ES\) criterion.

9.2 Envelope Theorem

This section introduces the Envelope theorem as a tool for calibrating the sensitivity of the optimal results to changes in exogenous (non-decision) variables. To this end, now introduce another variable, “\(a\)” for auxiliary, into the optimization problem, that represents the assumption that we wish to vary. So that you can appreciate this tool across various fields, this section provides a general introduction without a restriction to risk retention applications. Therefore, instead of focusing solely on risk retention problems such as in Display (9.1), we work with a modified version of a general problem from Display (3.9) given as: \[\begin{equation} \boxed{ \begin{array}{ccc} {\small \text{minimize}}_{\bf z} & f_0({\bf z} ,a) ,& \\ {\small \text{subject to}} & f_{con,j}({\bf z},a) \le 0 & j \in CON_{in} \\ & f_{con,j}({\bf z},a) = 0 & j \in CON_{eq} . \end{array} } \tag{9.2} \end{equation}\] In Display (9.2), both the objective function \(f_0\) and any of the constraint functions \(f_{con,j}\) may depend on the auxiliary variable \(a\). To emphasize, \(a\) is not one of the variables that is used in the optimization; the decision or choice variables are still represented by the vector \({\bf z}\). The interest lies in calibrating the sensitivity of the optimization results to changes in \(a\).

Active Sets of Constraints. Assuming that the problem in Display (9.2) is resolved for a fixed \(a\), we now suppose that \({\bf z}^*(a)\) is a stationary point on the feasible set and that there exists a set of optimal Lagrange multipliers. At the solution, some of the inequalities are binding \(f_{con,j}[{\bf z}^*(a),a] = 0\), while others are not. For those not binding, a small movement in \(a\) may produce a small change in the constraint value but, because it is not binding, it will not affect the associated Lagrange multiplier. Thus, as we verify in the proofs, we can essentially ignore non-binding (at the solution) constraints in the sensitivity analysis. To ease notation, let \(m\) be the number of equality plus binding inequality constraints and use \(f_{con,j}\) for \(j= 1, \ldots, m\) for these constraints, and similarly for the Lagrange multipliers, \(LME_j\).

Define the differentials \(f_{0,a}({\bf z},a)=\partial_{a} f_0({\bf z},a)\) for \(j=1, \ldots, m\) and \(i=1, \ldots, p_z\), \[ \begin{array}{llll} &f_{con,j,a}({\bf z},a)=\partial_{a} f_{con,j}({\bf z},a) \ \ \ \text{and} \ \ \ &f_{con,j,i}({\bf z},a)=\partial_{z_i} f_{con,j}({\bf z},a) . \end{array} \] With this notation, we have a version of the

Envelope Theorem. Assuming the objective and constraint functions are sufficiently smooth, we have \[\begin{equation} \begin{array}{ll} \partial_{a} f_0[{\bf z}^*(a),a] = f_{0,a}[{\bf z}^*(a),a]+ \displaystyle\sum_{j=1}^m LME_j^*(a) ~ f_{con,j,a}[{\bf z}^*(a),a] ,\\ \end{array} \tag{9.3} \end{equation}\] where \[\begin{equation} \begin{array}{ll} f_{con,j,a}[{\bf z}^*(a),a]= -\displaystyle\sum_{i=1}^{p_z} f_{con,j,i}[{\bf z}^*(a),a] ~ \partial_{a} z_i^*(a) , \ \ \ j=1, \ldots, m . \end{array} \tag{9.4} \end{equation}\]

A sketch of the proof of the Envelope theorem is in Appendix Section 9.5.3. Many economic applications focus on the first equation (9.3), providing an expression for the rate of change in the optimal value of the function being optimized, \(f_0[{\bf z}^*(a),a]\). Note that the \(m\) equalities in equation (9.4) provide information about the trade-offs among the decision variable changes \(\left(~\partial_{a}z_i^*(a)~\right)\) at the optimum.

The Envelope theorem may seem complex, but many problems do not require this full generality. In some problems, the constraint functions are not affected by the auxiliary variable. In such instances, from equation (9.3), we observe that \(\partial_{a} f_0[{\bf z}^*(a),a] = f_{0,a}[{\bf z}^*(a),a]\), indicating that small changes in the optimal value of the objective function can be computed as a marginal change in the objective function evaluated at the optimum. Furthermore, we have \(f_{con,j,a}[{\bf z}^*(a),a]=0\) for the left-hand side of equation (9.4), making it easy to discern the trade-offs among the decision variable changes \(\left(~\partial_{a}z_i^*(a)~\right)\) at the optimum.

In other cases, the objective function is not affected by the auxiliary variable, and thus \(f_{0,a}[{\bf z}^*(a),a]=0\). This is illustrated in the following example.

---

Example 9.2.1. Maximal Risk Transfer Cost as an Auxiliary Variable. Consider the risk retention problem in Display (9.1), letting a generic risk measure \(RM\) of retained risks serve as the objective function so that \(f_0(z_0, \boldsymbol \theta) = RM[g({\bf X}; \boldsymbol \theta)]\). In addition, let the maximal risk transfer cost be the auxiliary variable, \(a = RTC_{max}\). Intuitively, if the budget constraint is not binding, then a small change in \(RTC_{max}\) will not have an effect on the optimization result. So, we assume that the budget constraint is binding. Further, for illustration purposes, let us assume that one of the thetas is at the boundary and, for simplicity, take it to be the first one so that \(\theta_1^*(a) = 0\). With this, we have \(m=2\) and with some mild smoothness assumptions can evaluate the differentials \[ \begin{array}{llllc} &f_{0,a}(\boldsymbol \theta,a)&=\partial_{RTC_{max}} RM[g({\bf X};\boldsymbol \theta)] &=& 0, \\ &f_{con,1,a}(\boldsymbol \theta,a)&=\partial_{RTC_{max}} [RTC(\boldsymbol \theta) - RTC_{max}] &=& -1\\ &f_{con,2,a}(\boldsymbol \theta,a)&=\partial_{RTC_{max}} [-\theta_1] &=& 0 .\\ \end{array} \] Using equation (9.3), we have \[ \partial_{RTC_{max}} ~RM[g({\bf X};\boldsymbol \theta^* )] = -LME_1^* ~. \] Thus, the first Lagrange multiplier captures the marginal change in the minimal value of the objective function, per unit change in the maximal risk transfer cost. Note, too, that the sign reinforces our intuition. Thus, small increases in the maximal risk transfer costs, \(RTC_{max}\), lead to small decreases in the uncertainty retained risk (as summarized by the risk measure); this is what we would expect.

---

Example 9.2.2. Interpreting ANU Lagrange Multipliers. Let us continue with Example 9.2.1 but now specialize this to the ANU situation developed in Example 7.3.1. The risk measure is \(ES\). Figure 9.3 summarizes some of the earlier optimization results but now augments these with the Lagrange multipliers. This table and plot show the negative relationship between \(RTC_{max}\) and the optimal value of \(ES\). This rate of change is captured by the Lagrange multiplier \(LME_1^*\).

Because the Lagrange multipliers are also calculated using simulation methods, we can see unevenness in the early and later values of \(RTC_{max}\) where the calculations are less precise. For many audiences, analysts will find it valuable to demonstrate the relationship between \(RTC_{max}\) and the optimal value of \(ES\) by giving a range over different values of \(RTC_{max}\), as in this example. However, it is also useful to be able to interpret the Lagrange multiplier as a partial derivative. In this way, an analyst can provide information about the rate of change with a single optimization. For example, consider the table that is part of Figure 9.3. If one only ran the optimization at \(RTC_{max}=866\), then we could interpret the corresponding \(LME_1=3.1\) to mean a decrease of 3.1 in the optimal \(ES\) for each unit increase in \(RTC_{max}\).

Figure 9.3: ANU Excess of Loss Optimization Results - ES Criterion

---

Extending the idea of interpreting Lagrange multipliers as partial derivatives, consider the following

Special Case. Perturbed Problem. By letting one of the equality constraints equal the auxiliary variable, we can investigate small changes in the effect of that constraint on the problem solution, as follows. Consider the problem: \[\begin{equation} \boxed{ \begin{array}{ccc} {\small \text{minimize}}_{{\bf z}} & f_0({\bf z}) ,& \\ {\small \text{subject to}} & f_{con,j}({\bf z}) \le 0 & j \in CON_{in} \\ & f_{con,k}({\bf z}) = a & \\ & f_{con,j}({\bf z}) = 0 & j \in CON_{eq}, j \ne k . \end{array} } \tag{9.5} \end{equation}\] From the Envelope Theorem, we have \(LME_k^*(a)\) \(= - \partial_{a} f_0[{\bf z}^*(a)]\). That is, the multipliers measure the sensitivity of the optimal value of the objective function to changes in the limiting values of the constraints.

In economics, one can interpret Lagrange multipliers as providing a natural measure of value of scarce resources. For example, one of the classical economic situations is the profit maximization problem where each variable represents an input (e.g., Simon and Blume (1994)). Then, the \(j\)th multiplier can be interpreted as the change in the maximum profit per unit change in the \(j\)th input. In this sense, it is sometimes known as the shadow price. See also Boyd and Vandenberghe (2004), Section 5.6.

Video: Section Summary

9.3 Sensitivity Analysis for Risk Retention Problems

Now consider the modified version of the risk retention problem from Display (9.1) \[\begin{equation} \boxed{ \begin{array}{ccl} {\small \text{minimize}_{{\bf z}=(z_0, \boldsymbol \theta)}} & f_0({\bf z},a) \\ {\small \text{subject to}} & f_{con,1}({\bf z},a) =RTC(\boldsymbol \theta,a) - RTC_{max} \le 0& \\ & {\bf P} \boldsymbol \theta \le {\bf p}_0 ~~.\\ \end{array} } \tag{9.6} \end{equation}\] Here, the objective function \(f_0\) and the first constraint \(f_{con,1}\) are potentially affected by the auxiliary variable \(a\).

The other \(m-1\) constraints \({\bf P} \boldsymbol \theta \le {\bf p}_0\) trace out edges of the feasible region. They can ensure non-negativity of retention parameters (e.g., \(\theta_j \ge 0\)), provide an upper bound on the parameters (e.g., \(\theta_j \le 1\)), or enforce a balance among the parameters (e.g., \(\theta_1+\cdots+\theta_p = 1\)). Recall that for sensitivity purposes, we only consider those constraints that are binding at the optimum. To simplify the presentation, I assume that the constraints \({\bf P} \boldsymbol \theta \le {\bf p}_0\) are not affected by \(a\). As these constraints do not depend on the auxiliary variable, \[ f_{con,j,a}({\bf z},a) = \partial_a f_{con,j}({\bf z},a) = 0, \] a partial derivative with respect to \(a\) is zero and they can be ignored for sensitivity analysis.

---

With only \(m=1\) binding constraint that is affected by the auxiliary variable \(a\), from the Envelope Theorem we have \[\begin{equation} \begin{array}{ll} \partial_{a} f_0[{\bf z}^*(a),a] = f_{0,a}[{\bf z}^*(a),a]+ LME_1^*(a) ~ f_{con,1,a}[{\bf z}^*(a),a] , \end{array} \tag{9.7} \end{equation}\] where \[\begin{equation} \begin{array}{ll} f_{con,1,a}[{\bf z}^*(a),a] = -\displaystyle\sum_{i=1}^{p_z} \partial_{z_i}\left. RTC({\bf z}, a)\right|_{{\bf z}={\bf z}^*(a)} ~ \partial_{a} z_i^*(a) . \end{array} \tag{9.8} \end{equation}\]

---

For interpretation, now consider the case where the budget constraint \(f_{con,1}\) does not depend on \(a\). This means that \[\begin{equation} \begin{array}{ll} \partial_{a} f_0[{\bf z}^*(a),a] = f_{0,a}[{\bf z}^*(a),a] .\\ \end{array} \tag{9.9} \end{equation}\] That is, to determine the partial derivative of the objective function at the optimal value, we need only determine the partial derivative of the objective function and then evaluate it at the optimal value. In addition, the left-hand side of equation (9.8) is 0. To illustrate the trade-off among sensitivities, assume that \(p_z=2\) which yields \[ \begin{array}{ll} \partial_{z_1}\left. RTC({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)} \times \partial_{a} z_1^*(a) = - \partial_{z_2}\left. RTC({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)} \times \partial_{a} z_2^*(a) . \end{array} \] Typically, as one optimal parameter changes, the other changes in a proportional (and opposite in sign) way, subject to the signs of the partial derivatives of the constraint function.

---

Example 9.3.1 Level of Confidence. For the risk retention problem in Display (9.6), take the confidence level as the auxiliary variable, \(a = \alpha\). Further assume that the confidence level does not affect the budget constraint, so \(f_{con,1,a}({\bf z},a)\) \(=\partial_{a} f_{con,1}({\bf z},a) = 0\).

The goal is to minimize the \(ES\) as the measure of uncertainty but one can use \(ES1_F(x)\) for the objective function as described in Section 7.2.2. In this case, with \(\alpha =a\), we have \[ \begin{array}{ll} f_{0\alpha}({\bf z},\alpha) &= \partial_{\alpha} ES1_{F({\bf z})}(z_0) = \partial_{\alpha} \left\{z_0 + \frac{1}{1-\alpha} \left\{\mathrm{E}[Y({\bf z}) - z_0]_+\right\} \right\} \\ &= \left(\frac{1}{1-\alpha}\right)^2 \left\{\mathrm{E}[Y({\bf z}) - z_0]_+\right\} . \\ \end{array} \] At the optimum (where \(z_0^*=VaR^*\) is the \(\alpha\) quantile), we can express this as \[ \begin{array}{ll} \left(\frac{1}{1-\alpha}\right)^2 \left\{\mathrm{E}[Y({\bf z}^*) - z_0^*]_+\right\} &= \frac{1}{1-\alpha}\left\{ES(z_0^*) - VaR^*\right\} . \\ \end{array} \] From this expression, we see that the derivative is non-negative, meaning that as the confidence level increases so does the optimal value of \(ES\).

To get information about allocation trade-offs, from equation (9.8) we have \[ \begin{array}{ll} 0= \displaystyle\sum_{i=1}^{p_z} \left.\partial_{z_i} RTC({\bf z})\right|_{{\bf z}={\bf z}^*} ~ \partial_{\alpha} z_i^*(\alpha) . \end{array} \] This reveals an interesting balance among the retention parameters that is driven by the risk transfer cost function.

---

Example 9.3.2. Level of Confidence and the ANU Case. Let us continue with Example 9.3.1 but now specialize this to the ANU situation developed in Example 7.3.1. The decision variables are \({\bf z} = (z_0, u_1, \ldots, u_p)\).

Figure 9.4 summarizes some of the earlier optimization results from Table 8.9 and Figure 8.6; it now augments these with the partial derivative of the optimal \(ES\). The fourth column of the table, labelled Deriv ES is given in changes in the percentages of \(\alpha\). These partial derivatives are consistent with the right-hand side plot of Figure 9.4.

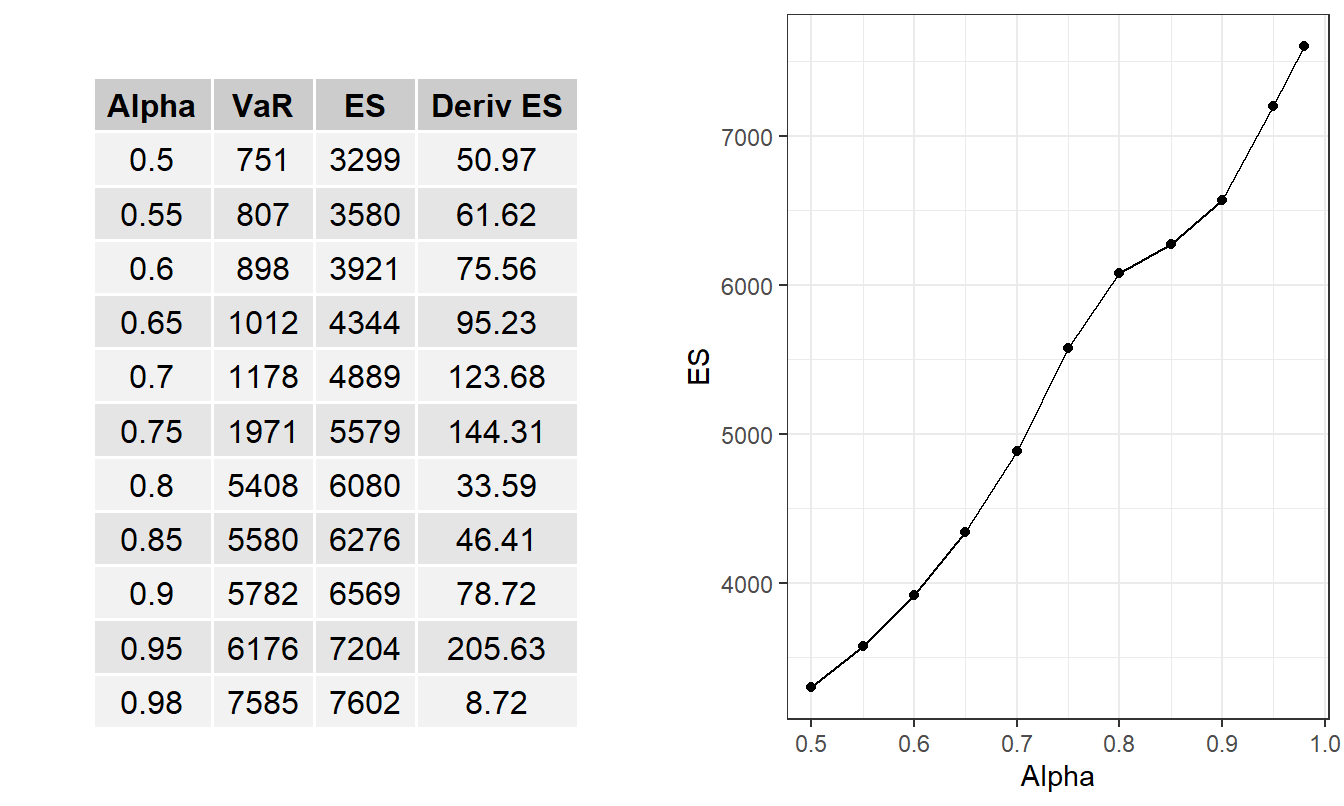
Figure 9.4: Retained Risk (measured by \(ES\)) versus Level of Confidence (measured by Alpha \(\alpha\)). Based on the ANU Excess of Loss Case Study where upper limits are determined by minimizing the \(ES\) criterion.

Assuming fair risk transfer costs, we have \(\partial_{u_j} RTC(u_1, \ldots, u_p) = \partial_{u_j} \mathrm{E}(X_j \wedge u_j) = 1 - F_j(u_j).\) Thus, \[ \begin{array}{ll} 0= \displaystyle\sum_{j=1}^p \left[ 1- F_j(u_j^*)\right] \times \partial_{\alpha} u_j^*(\alpha) . \end{array} \] This expression is interesting. In Figure 8.6 we saw the progressions of all upper limits. Further, the optimal retention policy changes the mixture of risks as \(\alpha\) changes; some of the \(u_j\) values increase as \(\alpha\) increases whereas others decrease. This expression provides greater insight into this trade-off of upper limit changes.

---

Example 9.3.3. Range Value at Risk and the ANU Case. For the risk retention problem in Display (9.6), now use the range value at risk \(RVaR\) for the objective function and let \(a=\beta\) be the auxiliary variable. Recall that \(\beta\) is the parameter that moves the \(RVaR\) between the \(VaR\) and the \(ES\).

From equation (2.4), if \(\beta>0\), we have \[ \begin{array}{ll} \partial_{\beta} ~RVaR_{(\alpha,\beta)}(X) & = \partial_{\beta} \left( \frac{1}{\beta} \int_{\alpha}^{\alpha + \beta} VaR_{z}(X) ~d z \right) \\ & = \frac{-1}{\beta^2} \int_{\alpha}^{\alpha + \beta} VaR_{z}(X) ~d z + \frac{1}{\beta} VaR_{\alpha + \beta}(X) \\ & = \frac{1}{\beta} \left\{ VaR_{\alpha + \beta}(X) - RVaR_{(\alpha,\beta)}(X) \right\} .\\ \end{array} \] As in Example 9.3.2, \(\beta\) does not affect the constraints and so equation (9.9) holds. \[ \begin{array}{ll} \partial_{\beta} ~RVaR_{(\alpha,\beta)}[g({\bf X}; {\bf z}^*)] & = \frac{1}{\beta} \left\{ VaR_{\alpha + \beta}[g({\bf X}; {\bf z}^*)] - RVaR_{(\alpha,\beta)}[g({\bf X}; {\bf z}^*)] \right\} ,\\ \end{array} \] where \({\bf z}^*={\bf z}^*(\beta)\).

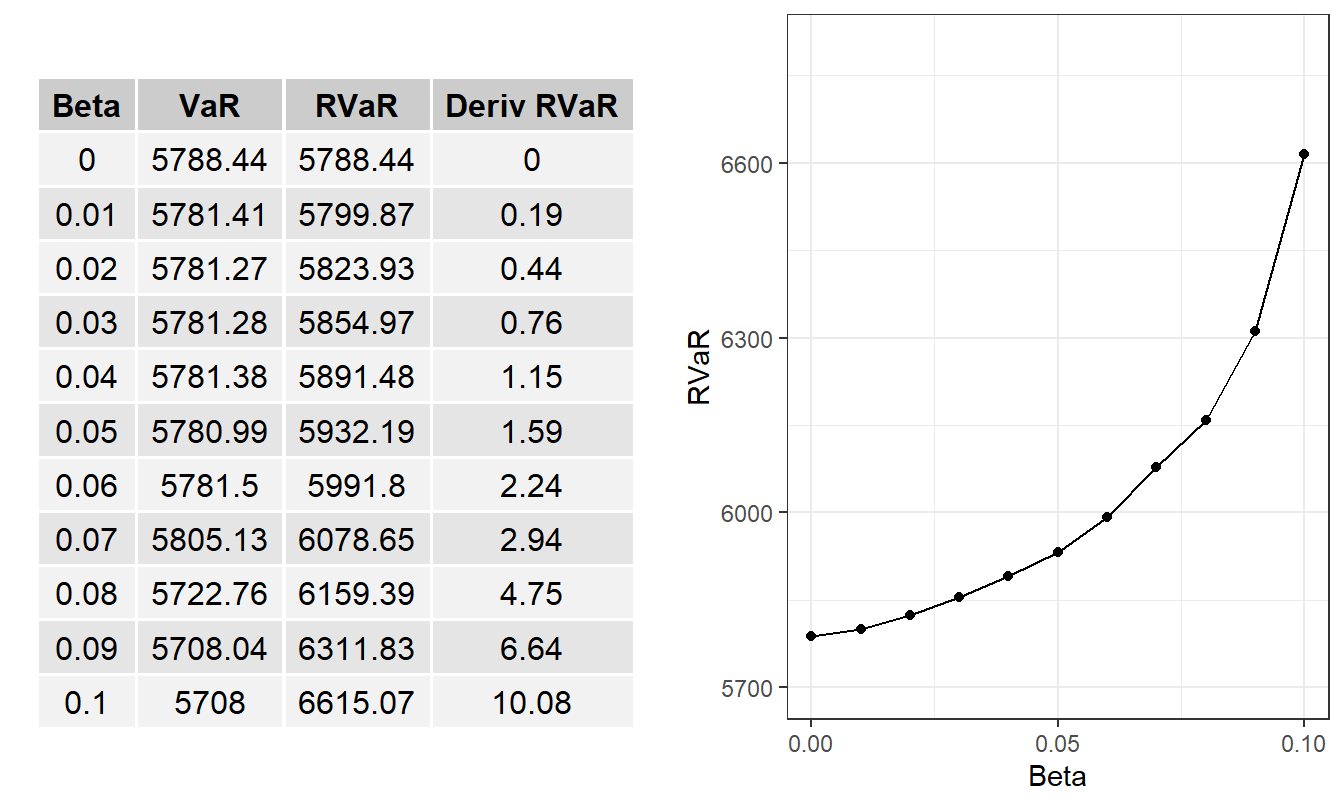
Figure 9.5: Retained Risk Measures versus Beta \(\beta\). Based on minimizing the \(RVaR\) criterion. Here, \(\beta=0\) corresponds to \(VaR\) and \(\beta=1-\alpha\) corresponds to \(ES\).

Figure 9.5 illustrates the steady increase in the optimal range value at risk as a function of the range parameter \(\beta\). The corresponding table also provides numerical values for the sensitivities that are small for small values of \(\beta\) and increase as \(\beta\) increases.

---

Example 9.3.4. Value at Risk Sensitivity. As we saw in Section 7.2.1, sometimes we can treat a risk measure as the solution of an optimization problem. In these cases, we can utilize the Envelope Theorem to quantify small changes in them and calibrate their sensitivity to auxiliary/exogenous changes.

Specifically, consider the problem in Display (9.1) where \(f_0(z_0) = z_0\) with \(m=1\) constraint \(f_{con,1}(z_0,{\bf z}) = -[F_{g(X;{\bf z})}(z_0) - \alpha]\). As we saw, the best value of \(z_0\) is \(z_0^* = F_{g(X;{\bf z})}^{-1}(\alpha)\) with corresponding Lagrange multiplier \(LMI_1^* = 1 / f_{g(X;{\bf z})}(z_0^*)\) (from the proof). For this example, we are only working with minimization over \(z_0\) and so may treat risk retention variables \(z_j\) as auxiliary variables.

With this, one can use the Envelope theorem to establish for any \(j=1, \ldots, p\), \[\begin{equation} \begin{array}{cl} \partial_{\theta_j} VaR_{\alpha}[g(X;{\bf z})] &= -\frac{1}{f_{g(X;{\bf z})}[F_{g(X;{\bf z})}^{-1}(\alpha)]} ~ \left. \partial_{\theta_j} F_{g(X;{\bf z})}(z_0) \right|_{z_0=F_{g(X;{\bf z})}^{-1}(\alpha)} .\\ \end{array} \tag{9.10} \end{equation}\]

\(Under~the~Hood.\) Check the \(VaR\) Sensitivity

For this problem, one minimizes over \(x\) and so we can take \(\theta_k =a\) to be an auxiliary variable. For partial derivatives, we use

• \(f_{0\theta_k}(x,\boldsymbol \theta)=\partial_{\theta_k} x =0\),
• \(f_{eq,\theta_k}(x,\boldsymbol \theta)=\partial_{\theta_k} f_{eq}(x,\boldsymbol \theta)=-\partial_{\theta_k} [F_{g(X;\boldsymbol \theta)}(x) - \alpha] =-\partial_{\theta_k} F_{g(X;\boldsymbol \theta)}(x)\), and
• \(f_{eq,1}(x,\boldsymbol \theta)=-\partial_{x} [F_{g(X;\boldsymbol \theta)}(x) - \alpha]=-f_{g(X;\boldsymbol \theta)}(x)\).

Thus, with (9.3), we have for any \(k=1, \ldots, p\)

\[ \begin{array}{cl} \partial_{\theta_k} VaR_{\alpha}(g(X;\boldsymbol \theta)) &= \partial_{\theta_k} f_0(x^*,\theta_k) \\ &= f_{0\theta_k}(x^*,\theta_k) + LME^* ~ f_{eq,\theta_k}(x^*,\theta_k) \\ &= 0 + LME^* ~ f_{eq,\cdot a}(x^*(a),a) \\ &= \frac{-1}{f_{g(X;\boldsymbol \theta)}[F_{g(X;\boldsymbol \theta)}^{-1}(\alpha)]} ~ \left. \partial_{\theta_k} F_{g(X;\boldsymbol \theta)}(x) \right|_{x=F_{g(X;\boldsymbol \theta)}^{-1}(\alpha)} ,\\ \end{array} \]

that confirms equation (9.10).

This corroborates the result established earlier in Section 5.3.1.

---

The right-hand side of equation (9.8) is a sum over the number of decision variables \(p_z\), not the number of random variables. For a multivariate example where the number of random variables exceeds the number of decision variables, consider the following:

Example 9.3.5. A Contract with Mixed Retention Functions. Consider 3 risk types, where the first risk, \(X_1\), is limited by an excess of loss policy with parameter \(u_1\) so the retained risk is \(X_1 \wedge u_1\). For the second risk, \(X_2\), a quota share is agreement is in place with parameter \(c_2\), so the retained risk is \(c_2 X_2\). For the third risk type, a per occurrence excess of loss agreement is in place with parameter \(u_3\), so the retained risk can be written as \(S(u_3) = \sum_{j=1}^N \{X_{2+j} \wedge u_3\}\), where \(N\) represents a random number of claims independent of the iid individual claims \(\left\{X_3, X_4, \ldots, \right\}\). With fair pricing, the cost of this insurance is \[ \begin{array}{ll} RTC(u_1,c_2,u_3) &= \mathrm{E} [X_1 + X_2 + S(\infty)] - \mathrm{E} \left\{ X_1 \wedge u_1 + c_2 X_2 + S(u_3)\right\} \\ &= \mathrm{E}(X_1) +\mathrm{E}(X_2) + \mathrm{E}(N) \mathrm{E}(X_3)\\ & \ \ \ - \left\{ \mathrm{E}(X_1 \wedge u_1) + c_2 \mathrm{E}(X_2) + \mathrm{E}(N) \times \mathrm{E}(X_3 \wedge u_3) \right\} . \end{array} \] The budget constraint is \(RTC(u_1,c_2,u_3) \le RTC_{max}\). If this constraint is binding at an optimal choice of retention parameters \(\{u_{1}^*,c_{2}^*,u_{3}^*\}\), then we can use equation (9.8) to investigate their relationship. Straightforward calculations yield \[ \begin{array}{ll} \partial_{u_1} RTC(u_1,c_2,u_3) &= - [1-F_1(u_1)] \\ \partial_{c_2} RTC(u_1,c_2,u_3) &= - \mathrm{E}(X_2) \\ \partial_{u_3} RTC(u_1,c_2,u_3) &= - \mathrm{E}(N) [1-F_3(u_3)] .\\ \end{array} \] With equation (9.8), we have \[ \begin{array}{ll} 0 & = [1-F_1(u_{1, opt})] ~\partial_{a} ~ u_{1, opt}(a) + \mathrm{E}(X_2) ~\partial_{a} ~c_{2, opt}(a) \\ & \ \ \ + \mathrm{E}(N) [1-F_3(u_{3, opt})] ~\partial_{a} ~u_{3, opt}(a) . \end{array} \] In this expression, \(a\) is a generic exogenous variable (not part of the budget constraint). For our applications, it could be a confidence level in the value at risk or expected shortfall or a parameter summarizing the dependence among risks. This expression provides an interesting balance among the decision variable sensitivities.

Video: Section Summary

9.4 Asset Allocation Sensitivity and Robustness

When examining the sensitivity to parameter assumptions, it is particularly intriguing to consider the asset allocation problem introduced in Section 1.3. Although this framework has been well received intellectually, its practical implementations have been limited, partly due to parameter uncertainty.

9.4.1 Asset Allocation Sensitivity

The asset allocation optimization model’s inputs include means, variances, and covariances/correlations, typically estimated from historical financial return data, as illustrated in Example 1.3.1. It is known that the optimal asset weights are highly sensitive to estimates of expected returns. Many investment managers find the optimal portfolio weights extreme and counter-intuitive (e.g., He and Litterman (2002)). Furthermore, the instability of these weights can result in poor out-of-sample performance for the optimal portfolio as demonstrated by De Prado (2016). Additionally, uncertainty in means can lead to highly concentrated portfolios. For instance, Best and Grauer (1991) demonstrate how slight changes in expected returns can result in heavy investments in one return balanced by a strong “negative” investment (shorting an asset) when assets are correlated.

Diversification of a portfolio of assets is one of the primary objectives of asset allocation, with variances and covariances at the core of this theory. Unfortunately, these inputs are also subject to estimation error which can lead to unstable portfolio weights. Interestingly, Chopra and Ziemba (1993) find that uncertainty in expected returns is roughly ten times as impactful as uncertainty in the covariance matrix. Additionally, the variance–covariance matrix can become unstable as asset correlations increase, which occurs precisely when diversification is crucial and yet more difficult to achieve (De Prado (2016)).

As summarized in Beketov, Lehmann, and Wittke (2018), in practical applications, all optimization model inputs are adjusted, substituted, and/or complemented by various methods, including robo-advising methods outlined in Section 6.5. One objective of this section is to put forth a method for quantifying the sensitivity of these inputs using methods developed earlier in the chapter.

To this end, building on the notation from Section 3.4, we now let \(\boldsymbol \mu\) be the vector of mean returns and, as before, let \(\boldsymbol \Sigma\) be the variance-covariance matrix. We wish to minimize the objective function as \(f_0({\bf c}, \boldsymbol \Sigma)\) \(= -\left({\bf c}^{\prime} \boldsymbol \mu - \lambda_{Port} ~ {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right)\) subject to a single (\(m=1\)) budget constraint \(f_{con,1}({\bf c}) = {\bf c}^{\prime}\mathbf{1} - 1=0\). In this minimal setting with no requirement that the allocation parameters be nonnegative, closed-form expressions for the sensitivities can be obtained, providing intuition for the results.

To begin, consider the uncertainty arising from mean parameters and choose the auxiliary variable to be \(a=\mu\), where \(\mu\) is an element of \(\boldsymbol \mu\) and use \(\partial_{\mu} \boldsymbol \mu\) for the change in the vector with respect to that element. So, for example, if \(\mu\) is the first mean, then \(\partial_{\mu} \boldsymbol \mu = {\bf 1}_1\) which represents a vector with 1 in the first entry and 0 for the other entries. Then, one can use first principles to establish \[\begin{equation} \begin{array}{rl} \partial_{\mu} {\bf c}^*(\mu) = \frac{1}{2\lambda_{Port}} \boldsymbol \Sigma^{-1}\left\{ [\partial_{\mu} \boldsymbol \mu] - {\bf 1} ~\partial_{\mu} LMI_1^*(\mu) \right\} \end{array} \tag{9.11} \end{equation}\] and \[\begin{equation} \partial_{\mu} LMI_1^*(\mu) = \frac{{\bf 1}^{\prime} \boldsymbol \Sigma^{-1} [\partial_{\mu} \boldsymbol \mu]}{{\bf 1}^{\prime} \boldsymbol \Sigma^{-1} {\bf 1}} .\\ \tag{9.12} \end{equation}\]

\(Under~the~Hood.\) Show Verification of Asset Allocation Sensitivities

The Lagrangian is

\[ \begin{array}{rl} LA &= f_0({\bf c}, \boldsymbol \Sigma) + LME_1 ~f_{con}({\bf c})\\ &= -\left({\bf c}^{\prime} \boldsymbol \mu - \lambda_{Port} ~ {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right) + LME_1({\bf c}^{\prime}\mathbf{1}- 1 ) .\\ \end{array} \]

To determine the optimal choice variables \(\bf c\), we take partial derivatives

\[ \begin{array}{rl} \partial_{\bf c} LA &= - \boldsymbol \mu + 2\lambda_{Port} ~ \boldsymbol \Sigma {\bf c} + LME_1~\mathbf{1} = {\bf 0}\\ \implies &{\bf c}^* = \frac{1}{2\lambda_{Port}}~ \boldsymbol \Sigma ^{-1}( \boldsymbol \mu - LME_1^*~\mathbf{1}) . \end{array} \]

In addition, from the constraint \({\bf c}^{\prime}\mathbf{1}=1\), we have

\[ \begin{array}{rl} &1= {\bf c}^{*\prime}\mathbf{1} = \frac{1}{2\lambda_{Port}}( \boldsymbol \mu - LME_1^*~\mathbf{1})'\boldsymbol \Sigma^{-1}\mathbf{1} \\ \implies &LME_1^* = [\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1} - 2\lambda_{Port}] / \mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} . \end{array} \]

Taking a partial derivative with respect to \(\mu\) is sufficient for equation (9.12).

In the same way, taking a partial derivative with respect to \(\mu\) of the optimal decision variables yields

\[ \begin{array}{rl} \partial_{\mu} {\bf c}^* = \frac{1}{2\lambda_{Port}}~ \boldsymbol \Sigma ^{-1}( \partial_{\mu}\boldsymbol \mu - \mathbf{1}~ \partial_{\mu}LME_1^*(\mu)) , \end{array} \]

which is sufficient for equation (9.11).

---

With this, the portfolio sensitivity for the mean, variance, and standard deviation are \[ \begin{array}{rl} \partial_{\mu} \left[\boldsymbol \mu'{\bf c}^*\right] &= \boldsymbol \mu' [\partial_{\mu} {\bf c}^*] + [\partial_{\mu} ~\boldsymbol \mu ]^{\prime} {\bf c}^{*} \\ \partial_{\mu} \left[{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}\right] &= [\partial_{\mu} {\bf c}^{*}]' \boldsymbol \Sigma {\bf c}^{*} + {\bf c}^{*\prime} \boldsymbol \Sigma [\partial_{\mu} {\bf c}^{*}] \\ \partial_{\mu} \sqrt{{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}} &= \frac{1}{2 \sqrt{{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}} }~~ \partial_{\mu} [{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}] = \partial_{\mu}~ SD[c^{*'}X] , \end{array} \] that can be evaluated using equations (9.11) and (9.12).

Example 9.4.1. Allocation Sensitivities for a Portfolio of Insurance Stock Returns. This is a continuation of Example 4.4.1 which is based on Example 1.3.1 and Example 3.4.1. However, unlike these earlier examples, we now no longer require nonnegative allocation parameters.

Table 9.2 summarizes results. The first two rows provide estimates of the mean and standard deviation based on five years of the training sample. These are annualized estimates based on daily data.

The third row provides the optimal allocation parameters \({\bf c}^*\) using a penalty parameter \(\lambda_{Port}=5\) as in Example 3.4.1. Note that the estimate for the French insurer AXA is negative, suggesting a negative investment or “shorting” this asset. For benchmarking, the optimal portfolio mean is 0.197 and the corresponding standard deviation is 0.126.

The fourth row provides allocation coefficient sensitivities for that risk. For example, if the mean for United Health increases by 1 unit (holding other means fixed), then the allocation for United Health increases by 1.262. The allocation parameters for the other seven stocks also change as displayed in Table 9.3.

The fifth and sixth rows of Table 9.2 display the marginal changes of the portfolio mean and standard deviation for changes in each mean parameter. It is interesting to see that the changes in the standard deviations tend to be smaller in magnitude than mean changes.

Table 9.2: Mean Sensitivities to Asset Allocations

	United Health	AIA	Ping An	Chubb	Allianz	Aon	AXA	Tokio Marine
\(\mu\)	0.249	0.166	0.208	0.097	0.159	0.181	0.139	0.148
\(\sigma\)	0.213	0.239	0.264	0.160	0.193	0.169	0.241	0.267
\(c^*\)	0.269	0.125	0.080	0.005	0.270	0.329	-0.164	0.086
\(\partial_{\mu}~ c^*(\mu)\)	1.262	1.222	1.075	3.021	3.802	2.780	2.493	0.781
\(\partial_{\mu}~ [c^{*'}\mu]\)	0.405	0.107	0.122	-0.271	0.330	0.465	-0.229	0.071
\(\partial_{\mu}~ SD[c^{*'}X]\)	0.054	-0.007	0.017	-0.110	0.024	0.054	-0.026	-0.006

Table 9.3 provides more information about the allocation coefficient sensitivities. For example, as in the fourth row of Table 9.2, we see that if the mean for United Health increases by 1 unit (holding other means fixed), then the allocation for United Health increases by 1.262. Furthermore, the first row of Table 9.3 provides changes in allocations for the other risks, all due to the 1 unit increase in the mean of United Health. In particular, note that there is a significant decrease in the Chubb allocation, -0.517. For each row, the sum of these changes is zero due to the budget constraint \({\bf c}^{\prime}\mathbf{1} = 1\). Thus, the entire portfolio of asset allocations is highly sensitive to the uncertainty of even a single input mean, suggesting the need for more robust approaches as will be taken up in Section 9.4.2.

Table 9.3: Mean Sensitivities to Allocation Coefficients - \(\partial_{\mu}~ c^*(\mu)\)

	United Health	AIA	Ping An	Chubb	Allianz	Aon	AXA	Tokio Marine
United Health	1.262	-0.057	-0.055	-0.517	-0.165	-0.375	-0.035	-0.058
AIA	-0.057	1.222	-0.591	-0.102	-0.206	-0.055	-0.032	-0.178
Ping An	-0.055	-0.591	1.075	0.013	-0.122	-0.134	-0.051	-0.136
Chubb	-0.517	-0.102	0.013	3.021	-0.636	-1.799	0.125	-0.105
Allianz	-0.165	-0.206	-0.122	-0.636	3.802	-0.259	-2.294	-0.120
Aon	-0.375	-0.055	-0.134	-1.799	-0.259	2.780	-0.090	-0.068
AXA	-0.035	-0.032	-0.051	0.125	-2.294	-0.090	2.493	-0.116
Tokio Marine	-0.058	-0.178	-0.136	-0.105	-0.120	-0.068	-0.116	0.781

Show Example 9.4.1 Code

load(file= "Data/Chap1Data/InsurSectorReturns.Rdata")
load(file="Data/Chap1Data/Frontier.Rdata")

# Training period summary statistics
numTradingDays <- 252 # Approximately nrow(Return_trn)/5
Sigma  <- cov(Return_trn)*numTradingDays
StdDev <- sqrt(diag(Sigma))
Means  <- colMeans(Return_trn)*numTradingDays
#  Determine the optimal allocations

portfolioMarkowitz <- function(mu, Sigma, lmd = 5) {
  c.prop <- Variable(nrow(Sigma))
  prob   <- Problem(Maximize(t(mu) %*% c.prop - 
                               lmd*quad_form(c.prop, Sigma)),
                  constraints = list(#c.prop >= 0, 
                                     sum(c.prop) == 1))
  result <- solve(prob)
  c.prop <- as.vector(result$getValue(c.prop))
  names(c.prop) <- colnames(Sigma)
  return(c.prop)
}
LPort <- 10
cstar <- portfolioMarkowitz(mu=Means, Sigma=Sigma, lmd=LPort)

PortfolioMean     <- t(as.vector(Means)) %*% cstar
PortfolioVariance <- t(cstar) %*% Sigma %*% cstar
PortfolioStdDev   <- sqrt(PortfolioVariance)

SigmaInv   <- solve(Sigma)
one.vec    <- rep(1,8)
one.SigInv <- one.vec  %*% SigmaInv
sum.SigInv <- sum(one.SigInv) # sum(SigmaInv)
LMEmu.vec  <- one.SigInv/sum.SigInv
c.mu       <- matrix(0, nrow=8,ncol=8)
one.vec    <- rep(1,8) 

MeanPort.muvec     <- rep(0,8)
VariancePort.muvec <- rep(0,8)
for (iaux in 1:8){
  zero.vec         <- rep(0,8) -> oneone.vec
  oneone.vec[iaux] <- 1
  c.mu[iaux,]      <- 1/(2*LPort)*
                SigmaInv %*% (oneone.vec - one.vec*LMEmu.vec[iaux])
  MeanPort.muvec[iaux] <- t(as.vector(Means)) %*% c.mu[iaux,] + cstar[iaux]
  VariancePort.muvec[iaux] <- t(c.mu[iaux,]) %*% Sigma %*% cstar +
                                t(cstar)  %*% Sigma  %*% c.mu[iaux,]
  }

StdDevPort.muvec <- as.numeric(0.5 * PortfolioStdDev**(-1)) * VariancePort.muvec
AssetAllocMat <- rbind(Means, StdDev, cstar, diag(c.mu), MeanPort.muvec, StdDevPort.muvec)
rownames(AssetAllocMat) <- c("$\\mu$", "$\\sigma$", 
                        "$c^*$", "$\\partial_{\\mu}~ c^*(\\mu)$", 
                        "$\\partial_{\\mu}~ [c^{*'}\\mu]$",
                        "$\\partial_{\\mu}~ SD[c^{*'}X]$")                      
colnames(c.mu) <- colnames(AssetAllocMat) -> rownames(c.mu)
#rowSums(c.mu)  #  Sum of each row is zero, as anticipated 

Exercise 9.4.3 shows how to construct sensitivities due to variance and covariance parameters. Readers will find it interesting to compare these sensitivities to the mean sensitivities described above to re-affirm the industry perception that mean changes have a greater effect than variance and covariance changes.

9.4.2 Asset Allocation Robustness

Stress testing, such as illustrated in Section 8.2, and sensitivity analysis (via the Envelope Theorem) in the previous sections of this chapter, aimed to understand the impact of changes made to underlying assumptions on risk modeling results. In areas such as financial asset allocation problems, it is known that extensive estimation error can occur in parameters like means, variances, and covariances of stocks. This parameter uncertainty has prompted the development of alternative optimization techniques that guard against, or are robust to, this underlying parameter uncertainty.

To illustrate this robustness concept, let us consider the asset allocation problem outlined in Section 3.4. As we saw in that section, in asset allocations it is common to maximize expected returns subject to a penalty for the uncertainty, expressed as \[ {\small \text{maximize}}_{\bf c} \left\{ {\bf c}^{\prime} \boldsymbol \mu - \frac{LMI_1}{2} \times {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right\} . \] A robust version is \[\begin{equation} {\small \text{maximize}}_{\bf c} \left\{ {\small \text{minimize}}_{\boldsymbol \mu \in \bf U}\left({\bf c}^{\prime} \boldsymbol \mu \right) - \frac{LMI_1}{2} \times {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right\} . \tag{9.13} \end{equation}\] Here, \(\bf U\) represents the uncertainty set. Intuitively, the mean parameters are unknown and vary within the uncertainty set. The minimization step yields the worst portfolio mean within \(\bf U\). Practitioners perceive this as a conservative and hence prudent form of portfolio construction, with parameter uncertainty incorporated directly into the portfolio optimization process. This approach aims to maximize penalized worst-case portfolio returns.

In typical applications, the uncertainty set is centered about \(\bar{\boldsymbol\mu} = ( \bar{\mu}_1, \ldots, \bar{\mu}_p)\) and takes on one of two forms: \[ \begin{array}{ccccc} {\bf U} = \{ |\mu_j - \bar{\mu}_j| \le \xi_j, j=1, \ldots, p \}& ~~ & {\bf U} = \{ (\boldsymbol\mu - \bar{\boldsymbol\mu})^{\prime} \boldsymbol \Omega^{-1}(\boldsymbol\mu - \bar{\boldsymbol\mu})\le \kappa^2 \} .\\ {\small \textit{box uncertainty set}} &~~ & {\small \textit{quadratric uncertainty set}} \end{array} \] For the box uncertainty set, it can be shown (c.f., Yin, Perchet, and Soupé (2021)) that equation (9.13) reduces to \[ {\small \text{maximize}}_{\bf c} \left\{ {\bf c}^{\prime} \bar{\boldsymbol \mu} - \kappa ~\times \max_j(|c_j|) - \frac{LMI_1}{2} \times {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right\} . \] In the same way, for the quadratic uncertainty set, equation (9.13) reduces to \[ {\small \text{maximize}}_{\bf c} \left\{ {\bf c}^{\prime} \bar{\boldsymbol \mu} - \kappa \sqrt{{\bf c}^{\prime}\boldsymbol \Omega{\bf c}} - \frac{LMI_1}{2} \times {\bf c}^{\prime} \boldsymbol \Sigma {\bf c} \right\} . \] Both problems are convex, specifically, second-order cone programming problems and so can be readily solved with modern tools, c.f., Boyd and Vandenberghe (2004) (Section 4.4.2). In asset allocation applications, it is common to also introduce uncertainty sets for the variance-covariance parameters, see, for example, Yin, Perchet, and Soupé (2021). Moreover, because this is a convex optimization problem, it is straight-forward to add the convex constraints on allocation parameters described in Section 3.4.2.

---

Example 9.4.2. Robust Allocationss for a Portfolio of Insurance Stock Returns. This is a continuation of Example 9.4.1. We illustrate the variability based on the quadratic uncertainty set. As before, we use sample training data to estimate the baseline mean vector \(\bar{\boldsymbol \mu}\) and variance-covariance matrix \(\boldsymbol \Sigma\). The uncertainty associated with the means is assumed to be proportional to \(\boldsymbol \Sigma\), so \(\boldsymbol \Omega \propto \boldsymbol \Sigma\). This proportionality constant can be absorbed into the parameter \(\kappa\), so the constrained optimization problem of interest is \[\begin{equation} \boxed{ \begin{array}{ccc} {\small \text{maximize}}_{\bf c} & {\bf c}^{\prime} \bar{\boldsymbol \mu} - \kappa \sqrt{{\bf c}^{\prime}\boldsymbol \Sigma{\bf c}} - \frac{LMI_1}{2} \times {\bf c}^{\prime} \boldsymbol \Sigma {\bf c}\\ {\small \text{subject to}} & {\bf c}' {\bf 1} = 1 \\ & c_j \ge 0, \ \ \ \ j=1, \ldots, p . \end{array} } \tag{9.14} \end{equation}\] We are now ready to compute the portfolio specified Display (9.14) with the CVXR package.

R Code to Develop Robust Allocations

portfolioMarkowitzRobust <- function(mu_hat, Sigma_hat, kappa,  LME = 10) {
  N <- length(mu_hat)
  SqRootSig <- chol(Sigma_hat)  # t(SqRootSig) %*% SqRootSig = Sigma
  c.prop <- Variable(N)
  prob <- Problem(Maximize(t(c.prop) %*% mu_hat - kappa*norm2(SqRootSig %*% c.prop) 
                  - (LME/2)*( norm2(SqRootSig %*% c.prop) )^2),
                  constraints = list(c.prop  >= 0, sum(c.prop) == 1))
  result <- solve(prob)
  return(as.vector(result$getValue(c.prop)))
}

c_Markowitz            <- portfolioMarkowitzRobust(mu, Sigma, kappa = 0)
names(c_Markowitz)     <- colnames(Sigma)
c_all_Markowitz_robust <- cbind(c_Markowitz)

# multiple robust solutions
T_trn <- nrow(Return_trn)
kappa <- 1.0

c_Markowitz_robust_noisy <- portfolioMarkowitzRobust(mu, Sigma, kappa)
c_all_Markowitz_robust   <- cbind(c_all_Markowitz_robust, c_Markowitz_robust_noisy)

set.seed(357)
library(mvtnorm)
for (i in 1:2) {
  X_noisy <- rmvnorm(n = T_trn, mean = mu, sigma = Sigma)
  mu_noisy <- colMeans(X_noisy)
  c_Markowitz_robust_noisy <- portfolioMarkowitzRobust(mu_noisy, Sigma, kappa)
  c_all_Markowitz_robust   <- cbind(c_all_Markowitz_robust, c_Markowitz_robust_noisy)
}
colnames(c_all_Markowitz_robust) <- c("c_Markowitz", "c_robust_base", "c_robust_1", "c_robust_2")

Figure 9.6 summarizes results over four optimizations. The first is the Markowitz portfolio optimum, with \(\kappa=0\), that serves as a benchmark. The second is a base robust optimization using Display (9.14). For the third and fourth, we perturbed values of \(\bar{\boldsymbol \mu}\) by adding small Gaussian noise and used these perturbed values in the Display (9.14) optimization problem. Figure 9.6 shows that the three robust allocations are similar when compared to the Markowitz allocations.

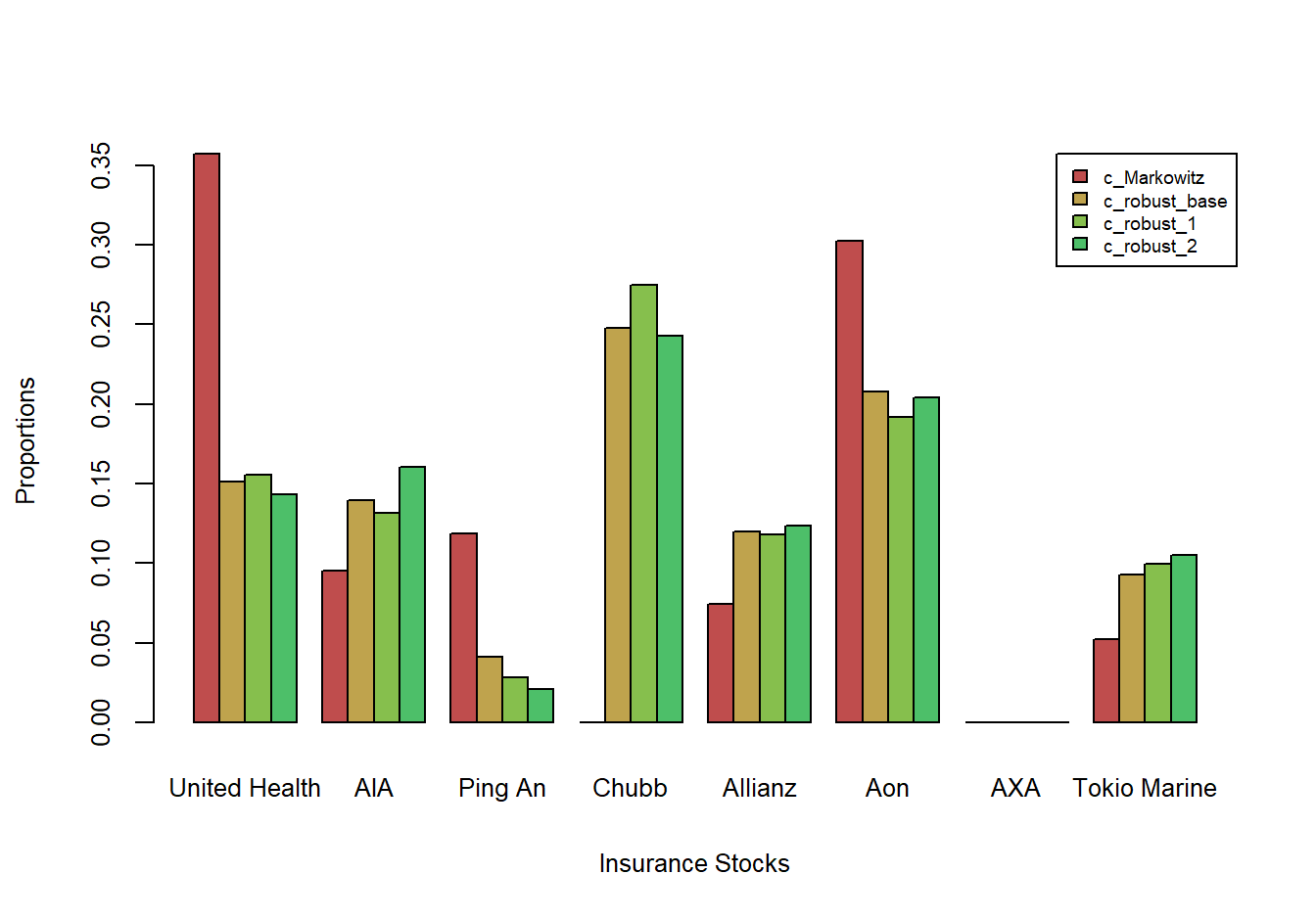
Figure 9.6: Four Sets of Robust Portfolio Allocations, by Insurer

Video: Section Summary

9.5 Supplemental Materials

9.5.1 Further Resources and Reading

Descriptions of the Envelope theorem may be found in standard mathematical economic textbooks such as Simon and Blume (1994) and in a handy online resource from Osborne (2021).

Descriptions of the investment portfolio problem have already been provided in Sections 1.3, 3.4, and 4.4.1. In addition to the references on this problem that appear in Section 9.4, another resource is Chalabi and Würtz (2015) for an introduction to portfolio allocation in R from an actuarial perspective. In the same spirit, Blanchet et al. (2019) provide an investigation of robustness in the context of insurance risk analysis.

9.5.2 Exercises

Section 9.2 Exercises

Exercise 9.2.1. Minimizing Risk Transfer Costs with an Auxiliary Level of Confidence and a \(VaR\) Constraint. This exercise switches the role of objective and (budget) constraint functions. The objective is to minimize risk transfer costs, \(f_0({\bf z}) =RTC({\bf z})\), subject to a constraint on the maximal value at risk, \(f_{con,1}[{\bf z}(\alpha),\alpha]\) \(= VaR_{\alpha}[{\bf z}(\alpha)] - VaR_{max}\) where \(VaR_{max}\) as a maximal allowed value at risk. Further, take the auxiliary variable to be the confidence level of the risk measure so \(a=\alpha\).

Thus, the objective function does not depend on the auxiliary variable. Use the Envelope Theorem to check that \[ \partial_{\alpha} RTC[{\bf z}^*(\alpha)] = LME_1^*(\alpha) ~ \frac{1}{f_{g(X;{\bf z}^*)}[VaR_{\alpha}({\bf z}^*(\alpha),\alpha)]} ,\\ \] where \(f_{g(X;{\bf z}^*)}(\cdot)\) is the probability density function of the random variable \(g(X;{\bf z})\) evaluated at the optimum \({\bf z}^*\). In problems we work with, typically \(LME_1^*>0\), indicating that \(\partial_{\alpha} RTC[{\bf z}^*(\alpha)]\) is also positive.

This is interesting because if \(f_0\) represents risk transfer costs and \(a\) represents a confidence level, then typically one would not think of the confidence level as affecting risk transfer costs. However, this special case shows that optimal cost does change through the changes in the optimal risk retention parameters \({\bf z}^*\).

Show Exercise 9.2.1 Solution

With \(f_0(\boldsymbol \theta) =RTC(\boldsymbol \theta)\), we have \(\partial_{\alpha} f_0(\boldsymbol \theta) =0\). For this application, \(m=1\) and so, from equation (9.3), we have

\[ \begin{array}{ll} \partial_{\alpha} f_0[\boldsymbol \theta^*(\alpha),\alpha] = 0+ LME_1^*(\alpha) ~ f_{con,1,\alpha}[\boldsymbol \theta^*(\alpha),\alpha] . \end{array} \]

Because \(f_{con,1}[\boldsymbol \theta(\alpha),\alpha]\) \(= VaR_{\alpha}[\boldsymbol \theta(\alpha)] - VaR_{max}\), we have \(f_{con,1,\alpha}[\boldsymbol \theta(\alpha),\alpha]\) \(= \partial_{\alpha} f_{con,1}[\boldsymbol \theta(\alpha),\alpha]\) \(=\partial_{\alpha} VaR_{\alpha}[\boldsymbol \theta(\alpha)]\). Thus,

\[ \begin{array}{ll} f_{con,1,\alpha}[\boldsymbol \theta(\alpha),\alpha] & = \partial_{\alpha} f_{con,1}[\boldsymbol \theta(\alpha),\alpha] =\partial_{\alpha} VaR_{\alpha}[\boldsymbol \theta(\alpha)] \\ & = \frac{1}{f_{g(X;\theta)}\left(VaR_{\alpha}[\boldsymbol \theta(\alpha)]\right)} \\ \end{array} \]

the required result.

For this last line, as we did in Section 5.3 we can assume some continuity and start with the relationship \(\alpha = F_{g(\mathbf{X};\theta)}\left(F_{g(\mathbf{X};\theta)}^{-1}(\alpha)\right)\). Differentiating both sides with respect to \(\alpha\) yields \(1 = f_{g(\mathbf{X};\theta)}\left(F_{g(\mathbf{X};\theta)}^{-1}(\alpha)\right) \partial_{\alpha} F_{g(\mathbf{X};\theta)}^{-1}(\alpha)\) where \(f(\cdot)\) is the probability density function corresponding to the distribution function \(F(\cdot)\). Thus, with the notation \(VaR_{\alpha}[g(\mathbf{X};\theta)] = F_{g(\mathbf{X};\theta)}^{-1}(\alpha)\) and equation (9.9), we have

\[ \begin{array}{ll} \partial_{\alpha} ~VaR_{\alpha}[g[\mathbf{X};\boldsymbol \theta^*(\alpha)] = \frac{1}{f_{g(\mathbf{X};\theta)}\left(VaR_{\alpha}[g[\mathbf{X};\boldsymbol \theta^*(\alpha)]\right)} .\\ \end{array} \]

---

Exercise 9.2.2. Minimizing Risk Transfer Costs with an Auxiliary Level of Confidence and an \(ES\) Constraint. Use the same set-up as in Exercise 9.2.1 but now use a constraint function in terms of the expected shortfall. Use the Envelope Theorem to show that \[ \partial_{\alpha} RTC[{\bf z}^*(\alpha)] = \frac{LME_1^*(\alpha)}{1-\alpha} \left\{ ES_{\alpha}({\bf z}^*(\alpha)) - VaR_{\alpha}({\bf z}^*(\alpha))\right\} . \] For interpretation, note that if \(LME_1^*>0\), then \(\partial_{\alpha} RTC({\bf z}^*(\alpha)) >0\). So, in many situations, an increase in the confidence level \(\alpha\) means an increase in the optimal risk transfer cost.

Show Exercise 9.2.2 Solution

From equation (2.3), we have

\[ \begin{array}{ll} \partial_{\alpha} ES_{\alpha}(X) &= \partial_{\alpha} \left(\frac{1}{1-\alpha} \int_{\alpha}^{1} VaR_{z}(X) d z \right) \\ &= \left( \partial_{\alpha}\frac{1}{1-\alpha} \right) \int_{\alpha}^{1} VaR_{z}(X) d z + \frac{1}{1-\alpha} \partial_{\alpha} \left(\int_{\alpha}^{1} VaR_{z}(X) d z \right) \\ &= \left( \frac{1}{(1-\alpha)^2} \right) \int_{\alpha}^{1} VaR_{z}(X) d z + \frac{1}{1-\alpha} \left( -VaR_{\alpha}(X)\right) \\ &= \frac{1}{1-\alpha} \left\{ ES_{\alpha}(X) - VaR_{\alpha}(X)\right\} .\\ \end{array} \]

Then, from equation (9.3), we have

\[ \partial_{\alpha} RTC[\boldsymbol \theta^*(\alpha)] = \frac{LME_1^*(\alpha)}{1-\alpha} \left\{ ES_{\alpha}(\boldsymbol \theta^*(\alpha)) - VaR_{\alpha}(\boldsymbol \theta^*(\alpha))\right\} , \]

the required result.

---

Exercise 9.2.3. Minimizing Risk Transfer Costs with an Auxiliary \(\beta\) and a \(RVaR\) Constraint. Use a similar set-up as in Exercises 9.2.1 and 9.2.2 but now assume the constraint function in terms of the range value at risk and take the auxiliary variable to be \(a=\beta\). Recall that \(\beta\) is the parameter that moves the \(RVaR\) between the \(VaR\) and the \(ES\). Use the Envelope Theorem to show that \[ \partial_{\beta} RTC[{\bf z}^*(\beta)] = \frac{LME_1^*(\beta)}{\beta} \left\{ VaR_{\alpha+\beta}[{\bf z}^*(\alpha)]-RVaR_{(\alpha,\beta)}[{\bf z}^*(\alpha)] \right\} . \] As in Exercises 9.2.1 and 9.2.2, in many situations (that is, \(LME_1^*>0\)), an increase in the parameter \(\beta\) means an increase in the smallest risk transfer cost. As \(VaR\) and \(ES\) represent opposite ends of the \(RVaR\) spectrum, we anticipate the smallest risk transfer costs for the expected shortfall measure to be larger than the small risk transfer costs for the value at risk measure.

Show Exercise 9.2.3 Solution

From equation (2.4), if \(\beta>0\), we have

\[ \begin{array}{ll} \partial_{\beta} RVaR_{(\alpha,\beta)}(X) & = \partial_{\beta} \left( \frac{1}{\beta} \int_{\alpha}^{\alpha + \beta} VaR_{z}(X) d z \right) \\ & = \frac{-1}{\beta^2} \int_{\alpha}^{\alpha + \beta} VaR_{z}(X) d z + \frac{1}{\beta} VaR_{\alpha + \beta}(X) \\ & = \frac{1}{\beta} \left\{ VaR_{\alpha + \beta}(X) - RVaR_{(\alpha,\beta)}(X) \right\} .\\ \end{array} \]

Then, from equation (9.3), we have

\[ \partial_{\beta} RTC[\boldsymbol \theta^*(\beta)] = \frac{LME_1^*(\beta)}{\beta} \left\{ VaR_{\alpha+\beta}[\boldsymbol \theta^*(\alpha)]-RVaR_{(\alpha,\beta)}[\boldsymbol \theta^*(\alpha)] \right\} , \]

the required result.

---

Exercise 9.2.4. Minimizing the \(VaR\) Using Distribution Functions. Consider the \(VaR\) minimization problem as in Display (7.3). Let the variable \(a\) represent an (as yet) unspecified auxiliary variable. Use the Envelope Theorem to show that \[\begin{equation} \begin{array}{ll} \partial_{a} VaR[g(X;{\bf z}^*),a] = \displaystyle\sum_{j=1}^2 LME_j^*(a) ~ f_{con,j,a}(z_0^*,{\bf z}^*,a) \ \ , \\ \end{array} \tag{9.15} \end{equation}\] where \(f_{con,1}(z_0,{\bf z},a) = -[F_{g(X;{\bf z})}(z_0) - \alpha ]\) and \(f_{con,2}(z_0,{\bf z},a) = RTC({\bf z}) - RTC_{max}\).

Show Exercise 9.2.4 Solution

From Display (7.3) and the Section 9.2 notation, we have

\[ \begin{array}{rl} f_0(z_0,\boldsymbol \theta,a) & = z_0\\ f_{con,1}(z_0,\boldsymbol \theta,a) & = -[F_{g(z_0;\boldsymbol \theta)}(z_0) - \alpha ] \\ f_{con,2}(z_0,\boldsymbol \theta,a) & = RTC(\boldsymbol \theta) - RTC_{max}.\\ \end{array} \]

Taking partial derivatives yields

• \(f_{0a}(z_0,\boldsymbol \theta,a)=\partial_{a} f_0(z_0,\boldsymbol \theta,a) = 0\),
• \(f_{con,1,a}(z_0,\boldsymbol \theta,a)=\partial_{a} f_{con,1}(\boldsymbol \theta,a) = -\partial_{a}[F_{g(X;\boldsymbol \theta)}(z_0) - \alpha ]\),
• \(f_{con,2,a}(z_0,\boldsymbol \theta,a)=\partial_{a} f_{con,2}(\boldsymbol \theta,a) = \partial_{a} [RTC(\boldsymbol \theta)- RTC_{max}]\),
• \(f_{con,1i}(z_0, \boldsymbol \theta,a)=\partial_{\theta_i} f_{con,1}(\boldsymbol \theta,a) = -\partial_{\theta_i}F_{g(X;\boldsymbol \theta)}(z_0)\), and
• \(f_{con,2i}(z_0, \boldsymbol \theta,a)=\partial_{\theta_i} f_{con,2}(\boldsymbol \theta,a) = \partial_{\theta_i}RTC(\boldsymbol \theta)\).

Thus, from equation (9.3) of the Envelope theorem, we have the result in equation (9.15) where

\[ {\small \begin{array}{lll} f_{con,1,a}(z_0^*,\boldsymbol \theta^*,a)&=\left. -\partial_{a}([_{g(X;\boldsymbol \theta)}(z_0) - \alpha ]\right|_{z_0=VaR^*(a)}&= \sum_{i=1}^p \left. \partial_{\theta_i}F_{g(X;\boldsymbol \theta)}(z_0)\right|_{z_0=VaR^*(a)} \times \partial_{a} \theta_i^*(a) \\ f_{con,2,a}(z_0^*,\boldsymbol \theta^*,a) &= \partial_{a} [RTC(\boldsymbol \theta)- RTC_{max}]&= -\sum_{i=1}^p \left. \partial_{\theta_i} RTC(\boldsymbol \theta) \right|_{\boldsymbol \theta=\boldsymbol \theta^*} \times \partial_{a} \theta_i^*(a). \\ \end{array} } \]

---

Exercise 9.2.5. Interpreting Multipliers. Continue with the Exercise 9.2.4 framework.

a. Now suppose in addition that the auxiliary variable is the confidence level for the value at risk, that is, \(a = \alpha\). Show that \(\partial_{\alpha} VaR^*(\alpha) = LME_1^*\). Interpret this result.
b. Now suppose in addition that the auxiliary variable is the maximal risk transfer cost, that is, \(a = RTC_{max}\). Show that \(\partial_{RTC_{max}} VaR^*(a) = - LME_2^*\). Interpret this result.

Show Exercise 9.2.5 Solution

For a generic auxiliary variable, note that

\[ \begin{array}{lll} f_{con,1,a}(z_0^*,\boldsymbol \theta^*,a)&=\left. -\partial_{a}[F_{g(X;\boldsymbol \theta)}(z_0) - \alpha ]\right|_{z_0=VaR^*(a)}\\ f_{con,2,a}(z_0^*,\boldsymbol \theta^*,a) &= \partial_{a} [RTC(\boldsymbol \theta)- RTC_{max}] .\\ \end{array} \]

a. With \(a=\alpha\), we see that \(f_{con,1\alpha}[z_0^*,\boldsymbol \theta^*(\alpha),\alpha]=1\) and \(f_{con,2\alpha}[z_0^*,\boldsymbol \theta^*(\alpha),\alpha]=0\). Thus, from equation (9.15), we have \(\partial_{\alpha} VaR^*(\alpha) = LME_1^*\). This means that we can interpret the first Lagrange multiplier to be the marginal change in the optimal value at risk per unit change in the level of confidence, \(\alpha\).

b. Similarly, suppose that the auxiliary variable is the maximal risk transfer cost, that is, \(a = RTC_{max}\). Then, \(f_{con,1\alpha}[z_0^*,\boldsymbol \theta^*(RTC_{max}),RTC_{max}]=0\) and \(f_{con,2RTC_{max}}[z_0^*,\boldsymbol \theta^*(RTC_{max}),RTC_{max}]= -1\). Thus, we have \(\partial_{RTC_{max}} VaR^*(RTC_{max}) = - LME_2^*\). This means that we can interpret the second Lagrange multiplier to be minus one times the marginal change in the optimal value at risk per unit change in the maximal risk transfer cost, \(RTC_{max}\).

Section 9.3 Exercises

Exercise 9.3.1. Compare Changes in the \(ES\) and \(GlueVaR\). Now we use a special case of \(GlueVaR\) for the objective function. Our first exposure to this flexible risk measure, due to Belles-Sampera, Guillén, and Santolino (2014), was in Exercise 2.4 where we saw that it exhibits many of the same qualities as the \(RVaR\). We now consider the special case \[ GlueVaR_{\omega}(X) = (1 -\omega) VaR_{\alpha}(X) + \omega ES_{\alpha}(X) , \ \ \ 0 \le \omega \le 1. \] Show that \[ \begin{array}{ll} \partial_{\alpha} ES_{\alpha}(X) &= \frac{1}{1-\alpha} \left\{ ES_{\alpha}(X) - VaR_{\alpha}(X)\right\} = \frac{1}{1-\alpha} ~\partial_{\omega} ~GlueVaR_{\omega}(X).\\ \end{array} \]

Show Exercise 9.3.1 Solution

Starting with equation (2.3), we have

\[ \begin{array}{ll} \partial_{\alpha} ES_{\alpha}(X) &= \partial_{\alpha} \left(\frac{1}{1-\alpha} \int_{\alpha}^{1} VaR_{z}(X) d z \right) \\ &= \left( \partial_{\alpha}\frac{1}{1-\alpha} \right) \int_{\alpha}^{1} VaR_{z}(X) d z + \frac{1}{1-\alpha} \partial_{\alpha} \left(\int_{\alpha}^{1} VaR_{z}(X) d z \right) \\ &= \left( \frac{1}{(1-\alpha)^2} \right) \int_{\alpha}^{1} VaR_{z}(X) d z + \frac{1}{1-\alpha} \left( -VaR_{\alpha}(X)\right) \\ &= \frac{1}{1-\alpha} \left\{ ES_{\alpha}(X) - VaR_{\alpha}(X)\right\} .\\ \end{array} \]

This is sufficient for the result.

---

Exercise 9.3.2. \(GlueVaR\) Risk Retention. Use the Envelope Theorem to show that \[ \begin{array}{ll} \partial_{\omega} ~GlueVaR_{\omega}[g({\bf X}; {\bf z}^*)] & = ES_{\alpha}[g({\bf X}; {\bf z}^*)] -VaR_{\alpha}[g({\bf X}; {\bf z}^*)] .\\ \end{array} \]

Show Exercise 9.3.2 Solution

Let \(a=\omega\) be the auxiliary parameter.

As in Section 9.3 examples, \(\omega\) does not affect any of the equality or binding inequality constraints and so equation (9.9) holds. Thus,

\[ \begin{array}{ll} \partial_{\omega} ~GlueVaR_{\omega}[g({\bf X}; \boldsymbol \theta^*)] & = ES_{\alpha}[g({\bf X}; \boldsymbol \theta^*)] -VaR_{\alpha}[g({\bf X}; \boldsymbol \theta^*)] .\\ \end{array} \]

---

Exercise 9.3.3. \(GlueVaR\) and the ANU Case. In Example 9.3.2, we used the \(RVaR\) measure to move smoothly between the two most well-known choices, the value at risk \(VaR\) and the expected shortfall \(ES\). In this way, we were able to calibrate the effects of using one measure versus the other. A simpler way of accomplishing this task is via the \(GlueVaR\) measure; in particular, the special case considered in Exercises 9.3.1 and 9.3.2 is simply a linear combination of the two measures.

Figure 9.7 shows although the optimal value of \(GlueVaR\) changes substantially with different choices of \(\omega\), the corresponding values of \(VaR\) and \(ES\) are relatively stable.

Create a table of values underpinning this figure, comparable to the work done in Example 9.3.3 for the \(RVaR\) measure. The table should summarize the optimization results over several different choices of the weight \(\omega\). Use \(\alpha=0.90\) for this demonstration. So, the row with \(\omega = 0\) will corresponds to \(VaR_{0.90}\) minimization and the row with \(\omega = 1\) corresponds to \(ES_{0.90}\) minimization. Your results should be similar to Table 9.4.

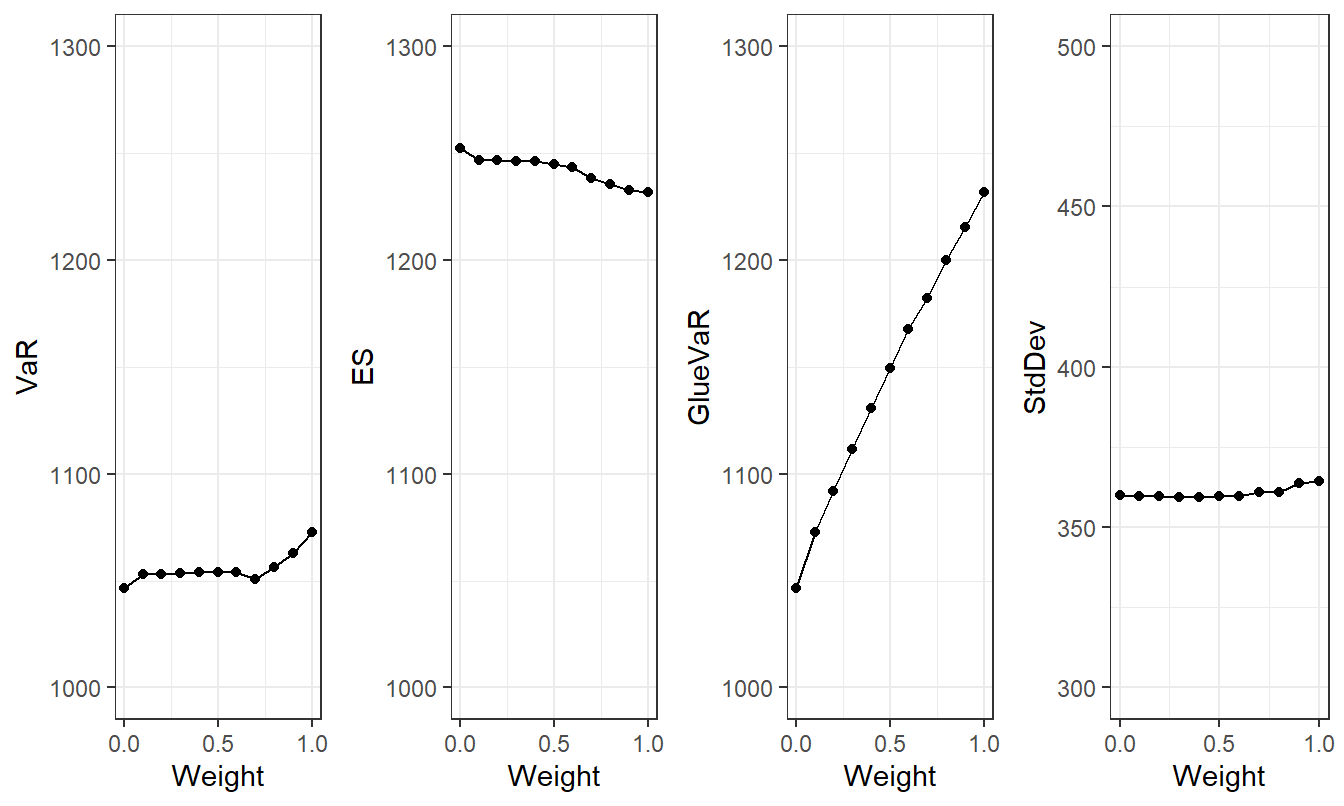
Figure 9.7: Retained Risk Measures versus Weight. Based on minimizing the \(GlueVaR\) criterion. Here, \(Weight=0\) corresponds to \(VaR\) and \(Weight=1\) corresponds to \(ES\).

Show Exercise 9.3.3 Solution

Table 9.4: ANU Excess of Loss Optimization - GlueVar Criterion - Varying Weight

Weight	\(RTC\)	\(VaR\)	\(ES\)	Std Dev	\(GlueVaR\)	\(LME\)	\(u_{1}\)	\(u_{2}\)	\(u_{3}\)
0.0	576	1047	1253	360	1047	2.61	596	178	130
0.1	576	1053	1247	360	1073	2.56	606	192	123
0.2	576	1053	1247	360	1092	3.24	607	189	126
0.3	576	1054	1246	360	1111	2.94	607	190	126
0.4	576	1054	1246	360	1131	3.64	607	192	124
0.5	576	1054	1245	360	1149	3.59	612	184	131
0.6	576	1054	1243	360	1168	3.61	614	199	125
0.7	576	1051	1238	361	1182	3.74	644	170	143
0.8	576	1056	1236	361	1200	3.66	656	176	141
0.9	576	1063	1233	364	1216	3.71	696	167	141
1.0	576	1073	1232	364	1232	3.72	708	157	139

#R Code for Changing Weight (w) in GlueVaR

alpha = 0.90
RMuw.fct <- function(u,w){
  RTC.R   <- 0 
  sumYj <- rep(0,nsim)
  for (j in 1:numVars){
    uj = as.numeric(u[j])    
    Yj    <- pmin(uj, Claims[,j])
    sumYj <- sumYj + pmin(uj, Claims[,j])
    RTC.R   <- RTC.R + mean(Claims[,j])- mean(Yj) 
    }
  VaR     <- quantile(sumYj, prob = alpha)
  CTE     <- VaR + ( mean(pmax(sumYj- VaR, 0)) )/(1-alpha)  
  StdDev <- sd(sumYj)
  GlueVaR <- (1-w)*VaR + w*CTE
  c(RTC.R, VaR, CTE, StdDev, GlueVaR)
}

time1 <- Sys.time()
Weightvec <- seq(from=0, to=1, length.out=11)

OutMat.GVaR  <- matrix(0,nrow = length(Weightvec), ncol = 7+numVars)  

u.names <- paste("$u_{",1:numVars, "}$", sep="")
colnames(OutMat.GVaR) <- c("Weight", "$RTC$", "$VaR$", "$ES$", 
                           "Std Dev", "$GlueVaR$", "$LM$", u.names)

starter.GVaR <- starter.u
  
for (jCost in 1:length(Weightvec)){
  Weight = Weightvec[jCost]
  RTC.GVaR <-  function(u){RMuw.fct(u,w=Weight)[1]}
  f0.GVaR  <-  function(u){RMuw.fct(u,w=Weight)[5]}
  hin.GVaR <- function(u) {h <- NA
    h[1] <- RTCmaxFix - RTC.GVaR(u)
    for (j in 1:numVars){h[j+1] <- u[j] } 
    return(h)}
  #if (jCost > 1){starter.GVaR <- GVaR.opt$par}
    GVaR.opt <- alabama::auglag(par=starter.GVaR, 
           fn=f0.GVaR,                          
           hin=hin.GVaR,                       
           control.outer=list(method="nlminb",trace=FALSE))
  uparams <- GVaR.opt$par
  output <- c(Weight, RMuw.fct(uparams,Weight), GVaR.opt$lambda[1], uparams)
  #cat("alabama results",output, "\n")    
  OutMat.GVaR[jCost,] <- output
  }
write.csv(OutMat.GVaR, file="Data/Chap9Tables/OutMatGVaR.csv")
Sys.time() - time1 

---

Exercise 9.3.4. \(GlueVaR\) and the ANU Case - Upper. As a follow-up to Exercise 9.3.3, develop a set of graphs that show the progression of upper limits as weights change. Your results should be similar to Figure 9.8.

This figure shows the progression of optimal upper limits as one moves from \(VaR\) minimization (\(\omega = 0\)) to \(ES\) minimization (\(\omega = 1\)). There is relatively little change in the limits. This provides a comforting result to risk managers; it suggests that the choice of the risk measure is not as critical. Put another way, the upper limit values are robust to this decision.

Show Exercise 9.3.4 Solution

Figure 9.8: Upper Limits versus Weight. Based on minimizing the \(GlueVaR\) criterion. Here, \(Weight=0\) corresponds to \(VaR\) and \(Weight=1\) corresponds to \(ES\).

Section 9.4 Exercises

Exercise 9.4.1. Quota Share. We now revisit the quota share agreement described in Section 4.3.2. As in that section, let \(\boldsymbol \Sigma\) denote the variance-covariance of risks and now let \(\boldsymbol \mu = \mathrm{E} (\mathbf{ X})\) denote their mean. For quota share with parameter \({\bf c} = {\bf z}\), the amount retained is \({\bf c}^{\prime} \mathbf{X}\) with uncertainty \(f_0({\bf c}, \boldsymbol \Sigma) = \mathrm{Var}({\bf c}^{\prime} \mathbf{X})={\bf c}^{\prime} \boldsymbol \Sigma {\bf c}\). There is a single (\(m=1\)) budget constraint based on \(f_{con,1}({\bf c}) = \boldsymbol \mu^{\prime}(\mathbf{1}- {\bf c}) -RTC_{max}\). The Lagrangian is \(LA = {\bf c}^{\prime} \boldsymbol \Sigma {\bf c}\) \(+ LME_1 [\boldsymbol \mu^{\prime}(\mathbf{1}-{\bf c}) - RTC_{max}]\). The auxiliary variable is \(\mu =a\), where \(\mu\) is an element of \(\boldsymbol \mu\). Further, let \(c^*\) be the optimal retention parameter corresponding to the choice of the \(\mu\).

Use first principles to establish \[\begin{equation} \partial_{\mu}{\bf c}^* = (\partial_{\mu}LME_1^*) \frac{1}{2}~\boldsymbol \Sigma^{-1} ~\boldsymbol \mu + \frac{LME_1^*}{2} ~\boldsymbol \Sigma^{-1} ~\partial_{\mu}\boldsymbol \mu \\ \tag{9.16} \end{equation}\] and \[\begin{equation} \partial_{\mu} ~LME_1^* = \frac{2}{\boldsymbol \mu^{\prime} \boldsymbol \Sigma^{-1} \boldsymbol \mu} \left[ 1 - LME_1^* ~ (\partial_{\mu} \boldsymbol \mu)^{\prime }~ \boldsymbol \Sigma^{-1} \boldsymbol \mu \right] . \\ \tag{9.17} \end{equation}\] Equation (9.16) provides a closed-form expression for quota share sensitivities using the Lagrange multiplier sensitivity in equation (9.17).

Show Exercise 9.4.1 Solution

To determine the optimal choice variables \(\bf c\), we take partial derivatives

\[ \begin{array}{rl} \partial_{\bf c}LA &= \partial_{\bf c}\left\{{\bf c}^{\prime} \boldsymbol \Sigma {\bf c}+ LME_1 [\boldsymbol \mu^{\prime}(\mathbf{1}-{\bf c}) - RTC_{max}] \right\}\\ & = 2 \boldsymbol \Sigma {\bf c}+ LME_1 ~\boldsymbol \mu \\ \implies & {\bf c}^* = \frac{LME_1^*}{2} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu . \end{array} \]

With the binding constraint \(f_{con}({\bf c}) = \boldsymbol \mu^{\prime}(\mathbf{1}- {\bf c}) -RTC_{max}\), we have

\[ \begin{array}{rl} RTC_{max} &= \boldsymbol \mu^{\prime}(\mathbf{1}- {\bf c}^*) \\ &= \boldsymbol \mu^{\prime}(\mathbf{1}- \frac{LME_1^*}{2} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu )\\ \implies& LME_1^* = 2(\boldsymbol \mu^{\prime}\mathbf{1} - RTC_{max}) / ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu ). \end{array} \]

Thus,

\[ \begin{array}{ll} \frac{1}{2} \partial_{\mu} ~LME_1^* &= \frac{1}{( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )^2} \left\{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu ) (1) - (\boldsymbol \mu^{\prime}\mathbf{1} - RTC_{max}) 2(\partial_{\mu} \boldsymbol \mu)^{\prime }~ \boldsymbol \Sigma^{-1} \boldsymbol \mu \right\} \\ &= \frac{1}{\boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu } \left\{ 1 - LME_1^* (\partial_{\mu} \boldsymbol \mu)^{\prime }~ \boldsymbol \Sigma^{-1} \boldsymbol \mu \right\} , \\ \end{array} \]

which is sufficient for equation (9.17).

In the same way, taking a partial derivative with respect to \(\mu\) of the optimal decision variables yields

\[ \begin{array}{rl} \partial_{\mu} {\bf c}^* &= \partial_{\mu} \left\{\frac{LME_1^*(\mu)}{2} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu \right\} \\ & = \frac{1}{2} \left\{ \left[\partial_{\mu} LME_1^*(\mu)\right] ~\boldsymbol \Sigma^{-1} \boldsymbol \mu +LME_1^*(\mu) ~\boldsymbol \Sigma^{-1} \left[ \partial_{\mu} \boldsymbol \mu \right] \right\} , \end{array} \]

which is sufficient for equation (9.16).

---

Exercise 9.4.2. Quota Share . Use the same set-up as in Exercise 9.4.1 except now take the auxiliary variable to be \(\sigma =a\), where \(\sigma\) is an element of \(\boldsymbol \Sigma\).

Use first principles to establish \[\begin{equation} \partial_{\sigma} {\bf c}^* = \frac{1}{2} \boldsymbol \Sigma^{-1}\boldsymbol \mu ~\partial_{\sigma} LME_1^* - \boldsymbol \Sigma^{-1} (\partial_{\sigma} \boldsymbol \Sigma){\bf c}^* \\ \tag{9.18} \end{equation}\] and \[\begin{equation} \partial_{\sigma} LME_1^* = \frac{2}{\boldsymbol \mu^{\prime}~\boldsymbol \Sigma^{-1}\boldsymbol \mu} \boldsymbol \mu^{\prime} \boldsymbol \Sigma^{-1} (\partial_{\sigma} \boldsymbol \Sigma){\bf c}^* . \tag{9.19} \end{equation}\]

Show Exercise 9.4.2 Solution

Starting with the optimal value of the Lagrange multiplier, we have

\[ \begin{array}{rll} \partial_{\sigma} LME_1^* &= 2 \partial_{\sigma} \frac{(\boldsymbol \mu^{\prime}\mathbf{1} - RTC_{max})}{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )} &=- 2 \frac{(\boldsymbol \mu^{\prime}\mathbf{1} - RTC_{max})}{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )^2} \partial_{\sigma} ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )\\ &=- \frac{LME_1^*}{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )} ( \boldsymbol \mu^{\prime}[\partial_{\sigma} \boldsymbol \Sigma^{-1} ]\boldsymbol \mu ) &= \frac{LME_1^*}{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )} ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1}[\partial_{\sigma} \boldsymbol \Sigma]\boldsymbol \Sigma^{-1} \boldsymbol \mu )\\ &= \frac{2}{ ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1} \boldsymbol \mu )} ( \boldsymbol \mu^{\prime}\boldsymbol \Sigma^{-1}[\partial_{\sigma} \boldsymbol \Sigma]\boldsymbol {\bf c}^* ) ,\\ \end{array} \]

which is sufficient for equation (9.19).

In the same way, taking a partial derivative with respect to \(\sigma\) of the optimal decision variables yields

\[ \begin{array}{rl} 2~ \partial_{\sigma} {\bf c}^* &= \partial_{\sigma} \left\{LME_1^*(\sigma)~\boldsymbol \Sigma^{-1} \boldsymbol \mu \right\} \\ &= \left\{ \partial_{\sigma} LME_1^*(\sigma) \right\} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu + LME_1^*(\sigma)~\left\{\partial_{\sigma} \boldsymbol \Sigma^{-1} \right\} \boldsymbol \mu \\ &= \left\{ \partial_{\sigma} LME_1^*(\sigma) \right\} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu - LME_1^*(\sigma)~\boldsymbol \Sigma^{-1}\left\{\partial_{\sigma} \boldsymbol \Sigma \right\} \boldsymbol \Sigma^{-1}\boldsymbol \mu \\ &= \left\{ \partial_{\sigma} LME_1^*(\sigma) \right\} ~\boldsymbol \Sigma^{-1} \boldsymbol \mu - 2~\boldsymbol \Sigma^{-1}\left\{\partial_{\sigma} \boldsymbol \Sigma \right\} {\bf c}^* ,\\ \end{array} \]

which is sufficient for equation (9.18).

---

Exercise 9.4.3. Asset Allocation. As a follow-up to Section 9.4.1, now the interest is in sensitivity due to the uncertainty parameters \(\sigma\). As background, Table 9.5 shows strong relationships among daily asset returns. This motivates the need to examine the effects of covariances as well as variances.

Table 9.5: Pearson Correlations among Daily Asset Returns

	United Health	AIA	Ping An	Chubb	Allianz	Aon	AXA	Tokio Marine
United Health	1.00	0.07	0.11	0.36	0.24	0.34	0.23	0.08
AIA	0.07	1.00	0.55	0.06	0.26	0.08	0.27	0.28
Ping An	0.11	0.55	1.00	0.09	0.28	0.14	0.28	0.28
Chubb	0.36	0.06	0.09	1.00	0.33	0.61	0.29	0.09
Allianz	0.24	0.26	0.28	0.33	1.00	0.32	0.80	0.25
Aon	0.34	0.08	0.14	0.61	0.32	1.00	0.30	0.10
AXA	0.23	0.27	0.28	0.29	0.80	0.30	1.00	0.28
Tokio Marine	0.08	0.28	0.28	0.09	0.25	0.10	0.28	1.00

a. Now choose the auxiliary variable to be \(a=\sigma\), where \(\sigma\) is an element of \(\boldsymbol \Sigma\). In the same way, prove that \[\begin{equation} \begin{array}{rl} \partial_{\sigma} {\bf c}^*(\sigma) = \frac{-1}{ 2 \lambda_{Port}} \boldsymbol \Sigma^{-1} {\bf 1} ~ \partial_{\sigma} LME_1^*(\sigma) - ~\boldsymbol \Sigma^{-1}(\partial_{\sigma} \boldsymbol \Sigma) {\bf c}^*(\sigma) \end{array} \tag{9.20} \end{equation}\] and \[\begin{equation} \partial_{\sigma} LME_1^*(\sigma) = 2 \lambda_{Port} \frac{ {\bf 1}^{\prime} \boldsymbol \Sigma^{-1} (\partial_{\sigma} \boldsymbol \Sigma) {\bf c}^*(\sigma) } { {\bf 1}^{\prime}~\boldsymbol \Sigma^{-1} {\bf 1} } . \\ \tag{9.21} \end{equation}\]

Show Exercise 9.4.3 Part (a) Solution

Recall from Section 9.4.1 that we have

\[ \begin{array}{rl} LME_1^* &= [\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1} - 2\lambda_{Port}] / \mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} \\ {\bf c}^* &= \frac{1}{2\lambda_{Port}}~ \boldsymbol \Sigma ^{-1}( \boldsymbol \mu - LME_1^*~\mathbf{1}). \end{array} \]

Starting with the optimal value of the Lagrange multiplier, we have

\[ \begin{array}{rll} \partial_{\sigma} LME_1^* &= \partial_{\sigma} \frac{(\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1} - 2\lambda_{Port})} { \mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} } \\ &=\frac{1}{(\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} )^2} \left[ (\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} ) \{ \partial_{\sigma} (\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1} - 2\lambda_{Port}) \}- (\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1} - 2\lambda_{Port}) \{ \partial_{\sigma}(\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} )\} \right] \\ &=\frac{1}{\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1}} \left[ \{ \partial_{\sigma} (\boldsymbol \mu '\boldsymbol \Sigma^{-1}\mathbf{1}) \}- LME_1^* \{ \partial_{\sigma}(\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1} )\} \right] \\ &=\frac{1}{\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1}} \left[ \{ -\boldsymbol \mu '\boldsymbol \Sigma^{-1}\{ \partial_{\sigma}\boldsymbol \Sigma \} \boldsymbol \Sigma^{-1}\mathbf{1} \} + LME_1^* \{\mathbf{1}'\boldsymbol \Sigma^{-1}\{ \partial_{\sigma}\boldsymbol \Sigma \} \boldsymbol \Sigma^{-1}\mathbf{1} \} \right] \\ &=\frac{1}{\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1}} \left[ LME_1^* ~\mathbf{1} -\boldsymbol \mu \right]' \boldsymbol \Sigma^{-1}\{ \partial_{\sigma}\boldsymbol \Sigma \} \boldsymbol \Sigma^{-1}\mathbf{1} \\ &=\frac{1}{\mathbf{1}'\boldsymbol \Sigma^{-1}\mathbf{1}} \left[{\bf c}^* (2 \lambda_{Port}) \right]' \{ \partial_{\sigma}\boldsymbol \Sigma \} \boldsymbol \Sigma^{-1}\mathbf{1} ,\\ \end{array} \]

which is sufficient for equation (9.21).

In the same way, taking a partial derivative with respect to \(\sigma\) of the optimal decision variables yields

\[ \begin{array}{rl} 2\lambda_{Port} ~\partial_{\sigma} {\bf c}^* &= \partial_{\sigma} \left[ \boldsymbol \Sigma ^{-1}( \boldsymbol \mu - LME_1^*(\sigma) ~\mathbf{1}) \right] \\ &= [\partial_{\sigma} \boldsymbol \Sigma ^{-1}] ( \boldsymbol \mu - LME_1^*(\sigma) ~\mathbf{1}) - \boldsymbol \Sigma ^{-1}[\partial_{\sigma} LME_1^*(\sigma)] ~\mathbf{1} \\ &= -[\boldsymbol \Sigma^{-1}\{ \partial_{\sigma}\boldsymbol \Sigma \} \boldsymbol \Sigma^{-1}] ( \boldsymbol \mu - LME_1^*(\sigma) ~\mathbf{1}) - \boldsymbol \Sigma ^{-1}[\partial_{\sigma} LME_1^*(\sigma)] ~\mathbf{1} \\ &= -\boldsymbol \Sigma^{-1}\{ \partial_{\sigma}\boldsymbol \Sigma \} {\bf c}^* (2 \lambda_{Port}) - \boldsymbol \Sigma ^{-1}[\partial_{\sigma} LME_1^*(\sigma)] ~\mathbf{1} , \\ \end{array} \]

which is sufficient for equation (9.20).

---

b. For the variance parameters, with \(a=\sigma\), the portfolio sensitivity for the mean, variance, and standard deviation are \[ \begin{array}{rl} \partial_{\sigma} \left[\boldsymbol \mu'{\bf c}^*\right] &= \boldsymbol \mu'[\partial_{\sigma} {\bf c}^*] \\ \partial_{\sigma} \left[{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}\right] &= [\partial_{\sigma} {\bf c}^{*}]' \boldsymbol \Sigma {\bf c}^{*} + {\bf c}^{*\prime} [\partial_{\sigma} \boldsymbol \Sigma]{\bf c}^{*} +{\bf c}^{*\prime}\boldsymbol \Sigma [\partial_{\sigma} {\bf c}^{*}] \\ \partial_{\sigma} \sqrt{{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}} &= \frac{1}{2 \sqrt{{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}} }~~ \partial_{\sigma} [{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}] = \partial_{\sigma}~ SD[c^{*'}X] , \end{array} \] that can be evaluated using equations (9.20) and (9.21). Use these relationships to confirm the sensitivities for these data as found in Tables 9.6 and 9.7.

Table 9.6 shows sensitivities for the mean portfolio \({\bf c}^{*\prime} \boldsymbol \mu\) for each of the 8 variance parameters and the 28 covariance parameters. (Note the symmetry in the table due to the covariance and that the diagonal elements are variances, not standard deviations.) Table 9.7 gives corresponding results for the standard deviation of the portfolio, \(\sqrt{{\bf c}^{*\prime} \boldsymbol \Sigma {\bf c}^{*}}\). As with the mean sensitivities in Table 9.2, it is interesting to see that the changes in the standard deviations tend to be smaller in magnitude than changes in the means.

Table 9.6: Portfolio Mean Variance Sensitivities

	United Health	AIA	Ping An	Chubb	Allianz	Aon	AXA	Tokio Marine
United Health	-1.11	-0.83	-0.67	0.66	-2.05	-2.65	1.32	-0.57
AIA	-0.83	-0.15	-0.25	0.31	-0.75	-0.98	0.49	-0.20
Ping An	-0.67	-0.25	-0.10	0.19	-0.61	-0.79	0.39	-0.17
Chubb	0.66	0.31	0.19	0.01	0.66	0.80	-0.40	0.21
Allianz	-2.05	-0.75	-0.61	0.66	-0.93	-2.43	1.20	-0.51
Aon	-2.65	-0.98	-0.79	0.80	-2.43	-1.57	1.56	-0.67
AXA	1.32	0.49	0.39	-0.40	1.20	1.56	-0.39	0.33
Tokio Marine	-0.57	-0.20	-0.17	0.21	-0.51	-0.67	0.33	-0.07

Table 9.7: Portfolio Standard Deviation Variance Sensitivities

	United Health	AIA	Ping An	Chubb	Allianz	Aon	AXA	Tokio Marine
United Health	0.29	0.27	0.17	0.01	0.58	0.70	-0.35	0.18
AIA	0.27	0.06	0.08	0.01	0.27	0.33	-0.16	0.08
Ping An	0.17	0.08	0.03	0.00	0.17	0.21	-0.10	0.05
Chubb	0.01	0.01	0.00	0.00	0.01	0.01	-0.01	0.00
Allianz	0.58	0.27	0.17	0.01	0.29	0.70	-0.35	0.18
Aon	0.70	0.33	0.21	0.01	0.70	0.43	-0.43	0.22
AXA	-0.35	-0.16	-0.10	-0.01	-0.35	-0.43	0.11	-0.11
Tokio Marine	0.18	0.08	0.05	0.00	0.18	0.22	-0.11	0.03

Show Exercise 9.4.3 Code Solution

LPort <- 10

MeanPort.sigmamat <- 0* cor(Return_trn)
VariancePort.sigmamat <- 0* cor(Return_trn)
for (iauxrow in 1:8){
  for (iauxcol in 1:8){ if (iauxrow <= iauxcol) {
  partialSig <-  matrix(0, nrow=8, ncol=8)   
  partialSig[iauxrow,iauxcol] <- 1 -> partialSig[iauxcol, iauxrow] 
  LMEsig <- as.numeric(2*LPort * one.SigInv %*% partialSig %*% cstar / sum.SigInv)
  c.sigAdd <- 1/(2*LPort) * SigmaInv %*% oneone.vec * LMEsig - 
                  SigmaInv %*% partialSig %*% cstar
  MeanPort.sigmamat[iauxrow, iauxcol] <- t(Means) %*% c.sigAdd -> MeanPort.sigmamat[iauxcol, iauxrow]
  Temp <- t(c.sigAdd) %*% Sigma %*% cstar +
        t(cstar) %*% partialSig %*% cstar + 
        t(cstar) %*% Sigma %*% c.sigAdd 
  VariancePort.sigmamat[iauxrow, iauxcol] <- Temp -> VariancePort.sigmamat[iauxcol, iauxrow]
  }}}
StdDevPort.sigmamat <- as.numeric(0.5 * PortfolioStdDev**(-1)) * VariancePort.sigmamat

---

9.5.3 Appendix. Establishing the Envelope Theorem

To establish the Envelope theorem, we use the Karush-Kuhn-Tucker (KKT) conditions that will be introduced in Section 11.1.

Starting with Display (9.2), we first re-label those inequalities that are binding at \({\bf z}^* (a)\) as equalities. With this adjustment in the notation, the associated Lagrangian \[\begin{equation} \begin{array}{cl} & LA\left({\bf z},a,\mathbf{LME},\mathbf{LMI}\right) \\ & = f_0({\bf z},a) + \displaystyle\sum_{j \in CON_{eq}} LME_j ~ f_{con,j}({\bf z},a) + \displaystyle\sum_{j \in CON_{in}} LMI_j ~ f_{con,j}({\bf z},a) \\ & = SLA\left({\bf z},a,\mathbf{LME}\right) + \displaystyle\sum_{j \in CON_{in}} LMI_j ~ f_{con,j}({\bf z},a), \\ \end{array} \tag{9.22} \end{equation}\] where \(SLA\) is the shortened version, omitting the (assumed to be non-binding) inequality constraints.

For each \(a\), suppose that \({\bf z}^*(a)\) is a local minimizer on the feasible set and that there exists Lagrange multipliers \(\mathbf{LME}^*(a) = \left(LME_j^*(a);~ j \in CON_{eq} \right)^{\prime}\) and \(\mathbf{LMI}^*(a) = \left(LMI_1^*(a);~ j \in CON_{in} \right)^{\prime}\) that satisfy the KKT conditions in Display (11.1), \[ \boxed{ \begin{array}{cl} LA_i \left[{\bf z}^*(a),a, \mathbf{LME}^*(a), \mathbf{LMI}^*(a) \right] = 0 \ \ \ \ & i=1, \ldots, p_z \\ f_{con,j}({\bf z}^*(a),a) = 0 & j \in CON_{eq} \\ LMI_j^*(a) = 0 & j \in CON_{in} ~.\\ \end{array} } \] We see that \(LMI_j^*(a) = 0\), \(j \in CON_{in}\), because these inequalities are assumed to be not binding at the optimum. So, for the purpose of developing the Envelope theorem, we can restrict consideration to the shortened version of the Lagrangian. Also note that this uses the notation \(LA_i\left[{\bf z},a,\mathbf{LME},\mathbf{LMI}\right]\) \(= \partial_{z_i} LA\left({\bf z},a,\mathbf{LME},\mathbf{LMI}\right)\).

We now establish equations (9.3) and (9.4).

\(Under~the~Hood.\) Sketch of Proofs of Equations (9.3) and (9.4)

Using the KKT conditions and taking a derivative of the equality constraint functions yields \[ \begin{array}{ll} 0&=\partial_{a} ~f_{con,j}[{\bf z}^*(a),a]\\ &= \displaystyle\sum_{i=1}^{p_z} \left\{\left. \partial_{z_i} f_{con,j}({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)} \times \partial_{a} z_i^*(a) \right\}+ \left. \partial_{a} f_{con,j}({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)} \\ &= \displaystyle\sum_{i=1}^{p_z} \left\{ f_{con,j,i}[{\bf z}^*(a),a] \times \partial_{a} z_i^*(a) \right\}+ f_{con,j,a}[{\bf z}^*(a),a] \\ \Rightarrow & f_{con,j,a}({\bf z}^*(a),a)= -\displaystyle\sum_{i=1}^{p_z} f_{con,j,i}[{\bf z}^*(a),a] \times \partial_{a} z_i^*(a) .\\ \end{array} \] This establishes equation (9.4).

With the Lagrangian \[ \begin{array}{ll} &LA_i\left[{\bf z},a,\mathbf{LME},\mathbf{LMI}\right] \\ &= \partial_{z_i} LA\left({\bf z},a,\mathbf{LME},\mathbf{LMI}\right) \\ &= \partial_{z_i} f_0({\bf z},a) + \displaystyle\sum_{j \in CON_{eq}} LME_j ~ \partial_{z_i} f_{con,j}({\bf z},a) \\ &~~~~~~~~~~~~~~~+ \displaystyle\sum_{j \in CON_{in}} LMI_j ~ \partial_{z_i} f_{con,j}({\bf z},a) \\ &= f_{0,i}({\bf z},a) + \displaystyle\sum_{j \in CON_{eq}} LME_j ~ f_{con,j,i} ({\bf z},a) \\ &~~~~~~~~~~~~~~~+ \displaystyle\sum_{j \in CON_{in}} LMI_j ~ \partial_{z_i} f_{con,j}({\bf z},a) .\\ \end{array} \] With the KKT conditions, \(LMI_j^*(a) = 0\), and so \[ \begin{array}{ll} &0= LA_i\left[{\bf z}^*(a),a,\mathbf{LME}^*(a),\mathbf{LMI}^*(a)\right] \\ \Rightarrow & f_{0,i}[{\bf z}^*(a),a] =- \displaystyle\sum_{j \in CON_{eq}} LME_j^*(a) ~ f_{con,j,i} [{\bf z}^*(a),a] .\\ \end{array} \] Next, we (a) take a derivative of the objective function at the optimum, then (b) insert the expression for \(f_{0,i}[{\bf z}^*(a),a]\) and finally (c) utilize equation (9.4). This yields \[ \begin{array}{ll} \partial_{a} f_0[{\bf z}^*(a),a] &= \displaystyle\sum_{i=1}^{p_z} \left\{\left. \partial_{z_i} f_0({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)} \times \partial_{a} z_i^*(a) \right\}+ \left. \partial_{a} f_0({\bf z},a)\right|_{{\bf z}={\bf z}^*(a)}\\ &= \displaystyle\sum_{i=1}^{p_z} \left\{ f_{0,i}[{\bf z}^*(a),a] \times \partial_{a} z_i^*(a) \right\}+ f_{0,a}[{\bf z}^*(a),a]\\ &= -\displaystyle\sum_{i=1}^{p_z} \left\{ \left[ \displaystyle\sum_{j \in CON_{eq}} LME_j^*(a) ~ f_{con,j,i} [{\bf z}^*(a),a]\right] \times \partial_{a} z_i^*(a) \right\}\\ &~~~~~~~~~~~~~~~+ f_{0,a}[{\bf z}^*(a),a]\\ &= - \displaystyle\sum_{j \in CON_{eq}} LME_j^*(a) \left\{ \displaystyle\sum_{i=1}^{p_z} f_{con,j,i} [{\bf z}^*(a),a]\times \partial_{a} z_i^*(a) \right\} \\ &~~~~~~~~~~~~~~~+ f_{0,a}[{\bf z}^*(a),a]\\ &= \displaystyle\sum_{j \in CON_{eq}} LME_j^*(a) ~ f_{con,j,a}[{\bf z}^*(a),a] + f_{0,a}[{\bf z}^*(a),a] ,\\ \end{array} \] as in equation (9.3).

---