Chapter 4 Transferring Multiple Risks including Reinsurance | Constructing Insurable Risk Portfolios

4.1 Reinsurance

As noted above, reinsurance is simply insurance purchased by an insurer. Insurance purchased by non-insurers is sometimes known as primary insurance to distinguish it from reinsurance. Reinsurance differs from personal insurance purchased by individuals, such as auto and homeowners insurance, in contract flexibility. Like insurance purchased by major corporations, reinsurance programs are generally tailored closely to the needs of the buyer. In contrast, in personal insurance buyers typically cannot negotiate on the contract terms although they may have a variety of different options (coverages) from which to choose.

The two broad types of agreements are proportional and non-proportional reinsurance. A proportional reinsurance contract is an agreement between a reinsurer and a ceding company (also known as the reinsured) in which the reinsurer assumes a given percent of losses and premiums. Non-proportional agreements are simply everything else. As examples of non-proportional agreements, this chapter looks first to stop-loss and excess of loss contracts and then to more complex arrangements.

A reinsurance contract can also be categorized as facultative or as a treaty. Facultative reinsurance contracts typically cover a single, large complex risk that cannot be readily grouped with other risks. In contrast, a treaty is a reinsurance contract that covers more than a specific risk, typically a specified share of all the insurance policies issued by the ceding company which come within the scope of the contract.

4.1.1 Proportional Reinsurance

The simplest example of a proportional treaty is called quota share. In a quota share reinsurance treaty, the reinsurer receives a flat percent, say 50%, of the premium for the book of business reinsured. In exchange, the reinsurer pays the same flat percent of losses, including allocated loss adjustment expenses.

For loss sharing, this is exactly the same as the risk retention agreement with a coinsurance parameter $c$ introduced in Section 2.2 where the insurer cedes a proportion $1-c$ of losses and retains the fraction $c$. However, in a quota share treaty, the premium is also specified as part of the treaty. Moreover, the insurer, or ceding company, has already incurred expenses for acquiring the business. Therefore, it is customary for the reinsurer to also pay the ceding company a ceding commission which is designed to reflect the differences in underwriting expenses incurred.

Quota share reinsurance treaties are particularly suitable for growing insurers or established companies which are new to a certain class of business. Quota share also makes sense for primary insurers who are seeking capital relief in light of solvency considerations or protection against random fluctuations across an entire portfolio. Because of their automatic nature, quota share treaties work well with high frequency lines of business. From the point of view of the reinsurer, quota share is desirable because the interests of the insurer and reinsurer are aligned and so there is little opportunity for moral hazard issues (such as sloppy claims handling).

From a theoretical viewpoint, we have already seen in Section 3.1 (Proposition 3.3) the desirability of the quota share contract for the reinsurer. There, we learned that the quota share reinsurance treaty minimizes the reinsurer’s uncertainty, measured by the variance, when subject to some mild constraints on the insurer’s variance of retained losses. Intuitively, quota share insurance is appealing because the insurer shares the responsibility for large losses in the tail of the distribution. As will be seen, this is in contrast to non-proportional agreements where reinsurers take responsibility for large losses.

4.1.1.1 Optimizing Quota Share Agreements for Insurers

As a variation, now assume $p$ risks in the portfolio, $X_1, \ldots, X_p,$ so that the portfolio sum is $S= X_1 + \cdots + X_p$. For simplicity, we now focus on the case of independent risks. Extensions to the dependent case are in Section 4.3. In a variation of the basic quota share agreement, the amount retained by the insurer may vary with each risk, say $c_i$. Thus, the insurer’s portion of the portfolio risk is $Y_{retained} = \sum_{i=1}^p c_i X_i$. What is the best choice of the proportions $c_i$? This is a question raised by De Finetti (1940).

To formalize this question, one seeks to find those values of $c_i$ that minimize $\mathrm{Var}(Y_{retained})$ subject to the constraint that $\mathrm{E}(Y_{reinsurer}) = RTC_{max}.$ The requirement that $\mathrm{E}(Y_{reinsurer}) = RTC_{max}$ suggests that the insurer wishes to spend a fixed quantity, say $RTC_{max}$, on the cost of reinsurance. Subject to this budget constraint, the insurer wishes to minimize the uncertainty of the retained risks as measured by the variance. Framed this way, this question is a constrained optimization problem. As only equality constraints are invoked, a solution can be derived using the Lagrange method.

The optimal proportions can be expressed as \[\begin{equation} c_{i}^* = \frac{LME^*}{2} \frac{\mathrm{E}(X_i)}{\mathrm{Var}(X_i)} , \tag{4.1} \end{equation}\] where \[\begin{equation} {\small LME^* = 2\left[\sum_{i=1}^p \mathrm{E}(X_i) -RTC_{max}\right] /\left[\sum_{i=1}^p \frac{[\mathrm{E}(X_i)]^2}{\mathrm{Var}(X_i)}\right]. } \tag{4.2} \end{equation}\]

$Under~the~Hood.$ Show the Verification of the Optimal Retention Proportions

Thus, the optimal proportion for the $i$th risk, $c_{i}^*$ is proportional to $\mathrm{E}(X_i)/\mathrm{Var}(X_i)$. This is intuitively appealing. Other things being equal, a higher revenue as measured by $\mathrm{E}(X_i)$ means a higher value of $c_i^*$. In the same way, a higher value of uncertainty as measured by $\mathrm{Var}(X_i)$ means a lower value of $c_i^*$. The proportional scaling factor is determined by the revenue requirement $\mathrm{E}(Y_{retained}) = RTC_{max}$. The following example helps to develop a feel for this relationship.

Example 4.1.1. Quota Sharing of Three Pareto Risks. Consider three risks that have a Pareto distribution, each having a different set of parameters (so they are independent but non-identical). Specifically, use the parameters:

$\alpha_1 =3$, $\theta_1=1,000$ for the first risk $X_1$,
$\alpha_2 =3$, $\theta_2=2,000$ for the second risk $X_2$, and
$\alpha_3 =4$, $\theta_3=3,000$ for the third risk $X_3$.

Figure 4.1 gives optimal values of $c_1$, $c_2$, and $c_3$ as the required risk transfer cost $RTC_{max}$ varies. Note that each coefficient decreases linearly with $RTC_{max}$ in accordance with equations (4.1) and (4.2).

Show Example 4.1.1 R Code

Figure 4.1: Quota Share Proportions versus Required Maximal Risk Transfer Cost

A limitation of this procedure is evident from Figure 4.1 where we see that some of coefficients exceed one. For example, for $RTC_{max} = 500$, we have $c_1^* =$ 1.143, $c_2^* =$ 0.571, and $c_3^* =$ 0.857. De Finetti (1940) was aware of this limitation and derived a complex expression for the optimal coefficients under the constraints $0 \le c_j \le 1$. See Exercise 10.1 for more details.

However, with tools available today, we now recognize the problem: \[ \boxed{ \begin{array}{lc} {\small \text{minimize}}_{c_1, \ldots, c_p} & \sum_i c_i^2 ~\mathrm{Var} (X_i) \\ {\small \text{subject to}} & \sum_i (1-c_i)~\mathrm{E} (X_i) = RTC_{max} \\ & 0 \le c_i \le 1, \ \ \ \ \ \ i=1, \ldots, p, \end{array} } \] as a quadratic programming problem where the objective function is a quadratic function and the constraints are linear in the coefficients. This is a type of convex problem, and so fast solvers are available. I describe this class of problems in Section 4.4.1. For now, the associated R code demonstrates a ready solution for an otherwise complicated problem. For Example 4.1.1, the solution turns out to be $c_1^* =$ 1.000, $c_2^* =$ 0.600, and $c_3^* =$ 0.900. Under the additional constraints, the objective function is 3,450,000. This is greater than the best value of the objective function without the additional constraints which turns out to be 3,428,571. This is as one would expect, when one introduces additional constraints, the region over which the function is to be minimized is smaller and so the optimal value must stay the same or increase.

Show Example 4.1.1 Follow-Up R Code

4.1.1.2 Surplus Share Proportional Treaty

Another proportional treaty is known as surplus share; this type of contract is common in commercial property insurance. This is essentially a type of variable quota share treaty where the sharing proportion c varies by risk type. As applied, typically the ceding insurer’s proportion is larger for smaller policies. In this way, the insurer can retain virtually all of the risk for small policies while seeking relief from the reinsurer for large risk types. Here is a common implementation:

The ceding company retains all risks with an insured amount below a given amount (the retained line).
The reinsurer is involved in risks where the insured amount exceeds the retained line. Up to a given limit (expressed as a multiple of the retained line, or number of lines), the ceding company’s proportion of the risk is the retained line as a fraction of the insured amount.
For risks in excess of the upper limit, the reinsurer’s proportion is the limit as a fraction of the insured amount.

For example, let the retained line be 100,000 and the given limit be six lines (600,000). Then, the proportion retained by the ceding company $c(IA)$ is a function of the insured amount ($IA$), as follows: \[ {\small \begin{array}{c|c|c} \hline \text{Insurance Amount} &\text{Reinsurer proportion} & \text{Insurer proportion}\\ IA &1-c(IA) & c(IA)\\ \hline IA \le 100000 &0 & 1 \\ 100000 < IA < 600000&\frac{IA-100000}{IA}& \frac{100000}{IA} \\ IA > 600000 & \frac{500000}{IA}&1-\frac{500000}{IA}\\ \hline \end{array} } \] As with quota share reinsurance, it is customary for the reinsurer to also pay the ceding company a ceding commission which is designed to reflect the differences in underwriting expenses incurred. Given the competitiveness of the marketplace for primary insurance, this premium is also insufficient causing primary insurers to operate at a loss. Thus, many reinsurers are adopting a procedure of returning to the ceding insurer only that part of the original premium that was not paid out in losses, cf. Swiss.Re (2013) (page 27).

Example 4.1.2. Surplus Share Retention for the Property Fund. Let us continue using the Property Fund data introduced in Example 2.1.1. In 2010, there were 1,095 policyholders that had positive coverage amounts. To illustrate, assume a retained line equal to 100 (in thousands) and a limit of six lines. For these data, it turns out that there are 981 policyholders with coverage below the retained line, 3 above the limit, and 111 in between. Figure 4.2 shows the surplus share retention as a function of insurance amount. Note the relatively low retention fractions for the three large policyholders.

Figure 4.2: Insurer’s Surplus Share Retention as a Function of Insurance Amount

4.1.2 Non-Proportional Reinsurance

The simplest example of a non-proportional treaty is called a stop-loss treaty. This acts as the same as the upper limit risk retention agreement introduced in Section 2.2. That is, the insurer sets a retention level $u$ and pays in full total losses for which $X \le u$. Further, for total losses for which $X > u$, the direct insurer pays $u$ and the reinsurer has responsibility for the remaining amount $X-u$. Thus, the insurer retains an amount $u$ of the risk. Summarizing, the amounts paid by the direct insurer and the reinsurer are $Y_{retained} = X \wedge u$ and $Y_{reinsurer} = \max(0,X-u) = (X-u)_+$. As before, note that $Y_{retained}+Y_{reinsurer}=X$. From a reinsurer’s perspective, note that $u$ could be considered a deductible. However, this book adopts the risk owner’s perspective and so $u$ represents the upper limit of its obligation.

Stop-loss, in its pure form, is not employed extensively in practice. This is likely due to its potential moral hazard weakness. With a pure stop-loss treaty, insurers have few incentives to carefully underwrite and monitor policies, as well as settle associated losses that contribute to experience above the stop-loss limit. Recall from basic economics that the phrase moral hazard is used to describe the situation where a contract alters the behavior of parties to the agreement. This would certainly be a concern to reinsurers that offer a stop-loss coverage. An exception to this is coverage between connected entities, such as a firm and its captive insurer, where incentives are aligned (see Section 6.2.2).

Nonetheless, at least conceptually, the stop-loss type of contract is particularly desirable for the insurer. As we learned in Section 3.1 (Proposition 3.4), the stop-loss reinsurance treaty minimizes the insurer’s uncertainty as measured by the variance subject to a mild budget constraint. Intuitively, with stop-loss insurance, the reinsurer takes responsibility for very large losses in the tail of the distribution, not the insurer.

Excess of Loss

A closely related form of non-proportional reinsurance is the excess of loss coverage. Under this contract, the total risk can be thought of as composed as $p$ separate risks $X_1, \ldots, X_p$ where each risk is subject to an upper limit, say, $u_i$. So the insurer retains \[ Y_{retained} = \sum_{i=1}^p X_i \wedge u_i = S(u_1, \ldots, u_p), \] and the reinsurer is responsible for the excess, $Y_{reinsurer}= S - Y_{retained}$. (Recall that the portfolio sum is $S= X_1 + \cdots + X_p$.) The retention limits may vary by risk or may be the same for all risks, that is, $u_i =u$ for all $i$. The development in this book focuses on this contract and so I introduce the notation $S(u_1, \ldots, u_p)$ to represent the sum of losses that are limited by the retention parameters $u_1, \ldots, u_p$.

In addition to arguments from theory, there are important practical considerations that recommend the use of non-proportional insurance to an insurer. Non-proportional insurance can limit an insurer’s liability with upper limits that reflect its willingness and capacity to bear risk. Smaller losses are the sole responsibility of the insurer and are not shared with the reinsurer, suggesting an insurer may focus its expertise on this portion of the portfolio and thus enhancing its earnings potential. In particular, administration costs can be lower for both parties as the insurer no longer needs to calculate the proportion of a loss for each risk as under surplus share reinsurance.

Optimal Choice for Excess of Loss Retention Limits

What are the best choices of the excess of loss retention limits $u_i$? One way to formalize this question is to find those values of $u_i$ that minimize $\mathrm{Var}(Y_{retained})$ subject to the constraint that $\mathrm{E}(Y_{reinsurer}) = RTC_{max}$. Subject to this budget constraint, the insurer wishes to minimize the uncertainty of the retained risks (as measured by the variance).

As before, only equality constraints are invoked and so a solution can be derived using the Lagrange method. Specifically, define the Lagrangian \[ \begin{array}{ll} LA &= \mathrm{Var}(Y_{retained}) + LME \{\mathrm{E}(Y_{reinsurer}) - RTC_{max} \} \\ &= \sum_{i=1}^p ~\mathrm{Var}(X_i \wedge u_i) + LME \{ [\sum_{i=1}^p ~\mathrm{E}(X_i)-\mathrm{E}(X_i \wedge u_i)]- RTC_{max}\}. \end{array} \]

$Under~the~Hood.$ Show the Optimal Excess of Loss Limits

Optimizing the function $LA$ over choices of upper limits provides insights into properties of the optimal retention limits $u_i^*$. In particular, it turns out that the optimal retention limit less the insurer’s expected retained losses, $u_i^* - E[X_i \wedge u_i^*]$, is the same for all risks. Gray and Pitts (2012) (Section 5.8) attribute the discovery of this result to Bruno de Finetti (1906-1985). Section 11.3.1 will provide extensions to additional contracts.

Example 4.1.3. Excess of Loss for Three Pareto Risks. Consider three risks that have a Pareto distribution, each having a different set of parameters (so they are independent but non-identical). Use the same set of parameters as in Example 4.1.1.

By minimizing the Lagrangian, one can numerically determine the optimal retention limits $u_1^*$, $u_2^*$, and $u_3^*$. This is done in the associated R code using the package alabama. Results from the numerical optimization show that each optimal retention limit minus expected insurer’s losses, $u_i^* - E[X_i \wedge u_i^*]$, is the same for all risks, as derived theoretically. In addition, one can graphically compare the distribution of total risks to that retained by the insurer and by the reinsurer, as displayed in Figure 4.3. This graph summarizes the distributions of possible outcomes that result from the optimal retention policy.

Show Example 4.1.3 R Code

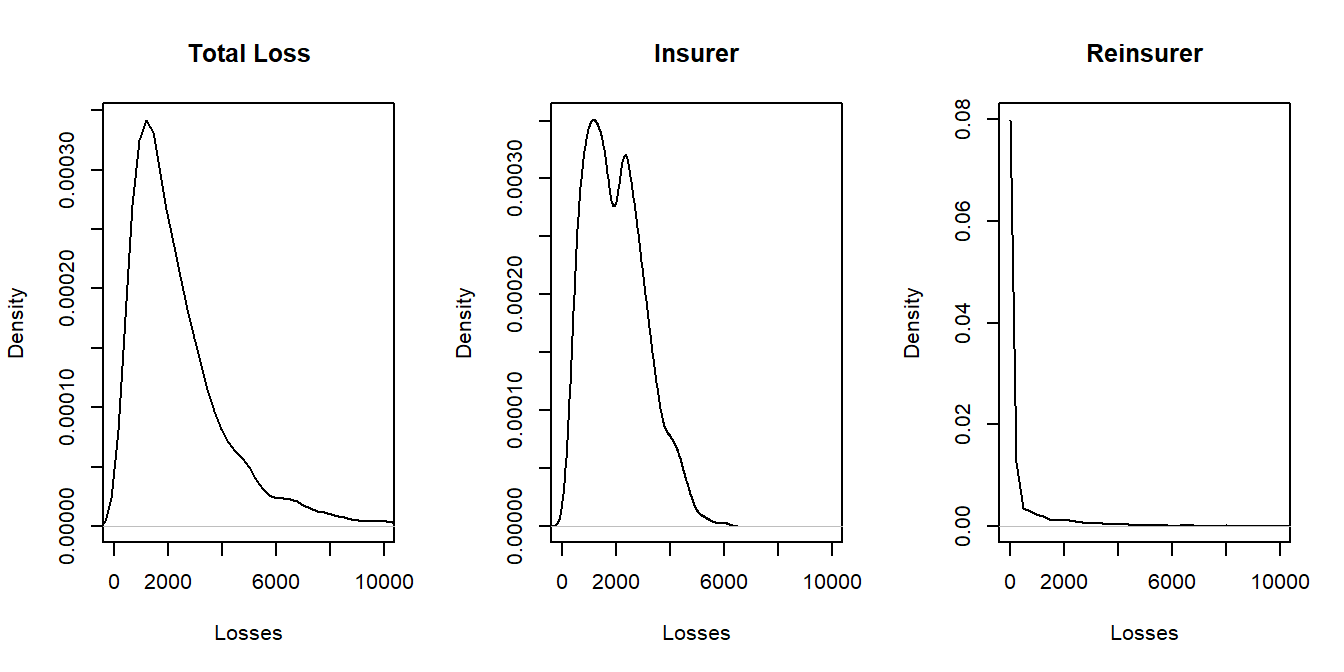
Figure 4.3: Density Plots for Total Loss, the Insurer, and the Reinsurer

4.1.3 Layers of Coverage

Typically excess of loss contracts limit the exposure for a reinsurer, as illustrated in the following example.

Example 4.1.4. Consider a specific risk of an insurer. For this risk, the reinsurer is responsible for losses in excess of 500 up to a limit of 100,000, that is, $Y_{reinsurer} =\min[(X-500)_+, 100000]$. The insurer retains the remaining risk, $Y_{retained} = X - Y_{reinsurer}$.

From the reinsurer’s point of view, in the language of Section 2.2 one would think of 500 as a “deductible” and 100,000 as its “upper limit” of coverage.

In reinsurance, it is common to partition loss amounts into multiple layers. This partitioning of losses is easiest to think about when there are more than two parties responsible for a risk, a concept further developed in Section 4.5. For example, instead of simply an insurer and reinsurer or an insurer and a policyholder, think about the situation with all three parties, a policyholder, insurer, and reinsurer, who agree on how to share a risk. More generally, consider $k$ parties. If $k=3$, it could be an insurer and two different reinsurers.

Example 4.1.5. Layers of Coverage for Three Parties.

Suppose that there are $k=3$ parties. The first party is responsible for the first 100 of losses, the second responsible for losses from 100 to 3000, and the third responsible for losses above 3000.
If there are four losses in the amounts 50, 600, 1800 and 4000, then they would be allocated to the parties as follows: \[ {\small \begin{array}{l|rrrrrrr} \hline \text{Layer}& \text{Claim 1}& \text{Claim 2}& \text{Claim 3}& \text{Claim 4}& \text{Total} \\ \hline (0, 100]& 50& 100& 100 & 100 & 350\\ (100, 3000]& 0& 500 & 1700 & 2900& 5100 \\ (3000, \infty)& 0 & 0 & 0 & 1000 & 1000\\ \hline \text{Total} & 50 & 600& 1800& 4000& 6450 \\\hline \end{array} } \]

To handle the general situation with $k$ groups, partition the positive real line into $k$ intervals using the cut-points \[ 0 = u_0 < u_1 < \cdots < u_{k-1} < u_k = \infty. \] Note that the $i$th interval is $(u_{i-1}, u_i]$. Now let $Y_i$ be the amount of risk shared by the $i$th party. To illustrate, if a loss $X$ is such that $u_{i-1} <X \le u_i$, then \[ \left(\begin{array}{c} Y_1\\ Y_2 \\ \vdots \\ Y_i \\Y_{i+1} \\ \vdots \\Y_k \end{array}\right) =\left(\begin{array}{c} u_1-u_0 \\ u_2-u_1 \\ \vdots \\ X-u_{i-1} \\ 0 \\ \vdots \\0 \end{array}\right) . \] More succinctly, we have \[ Y_i = \min(X,u_i) - \min(X,u_{i-1}) . \] With this expression, one can see that the $i$th party is responsible for losses in the interval $(u_{i-1}, u_i].$ With this, it is easy to check that $X = Y_1 + Y_2 + \cdots + Y_k.$ To illustrate, applying this structure to Example 4.1.4, we see that the primary insurer has responsibility for the first and third layers ($Y_1$ and $Y_3$) whereas the reinsurer has responsibility for the second layer ($Y_2$). Thus, the parties taking on different layers need not be different.

For an example used in practice, see the Wisconsin Property Fund site for an illustration of layers of reinsurance.

See Appendix Section 4.6.4 for an overview of a mathematical framework that provides conditions under which a layered coverage scheme is optimal.

4.1.4 Complexities of Reinsurance Coverage

Historically, reinsurance agreements were contracts negotiated based on individual risks. These contracts, done on a case-by-case basis, today are known as facultative reinsurance and continue to represent about 15% of the marketplace (in terms of premium volume), cf. Albrecher, Beirlant, and Teugels (2017). The remainder of the market has an obligatory treaty form, where both parties are bound by an obligation to cede and assume a contractually agreed share of a risk portfolio.

Because of their experience in risk modeling, reinsurers are key drivers in the adoption of better risk management practices by many organizations. Given their technical expertise and the extensive marketplace for unique contract arrangements, it is not surprising that reinsurance contracts can easily become quite complicated. This section describes a few of the more popular contracts.

To illustrate, some excess of loss contracts have in addition an (annual) aggregate deductible $AAD$ so that the reinsurer’s obligation may be written as \[ Y_{reinsurer} =\left[\left( \sum_{i=1}^p \min[(X_i-u_{1,i})_+, u_{2,i}]\right)- AAD\right]_+ . \] Here, $u_{1,i}$ represents a reinsurer’s deductible and $u_{2,i}$ represents is upper limit for the $i$th risk. Deductibles and upper limits may vary by risk or be the same. In the same way, excess of loss contracts may have an (annual) aggregate limit $AAL$, so that \[ Y_{reinsurer} = \min \left( \sum_{i=1}^p \min[(X_i-u_{1,i})_+, u_{2,i}], AAL \right) . \] Naturally, a contract may have both an overall deductible and an upper limit. Albrecher, Beirlant, and Teugels (2017) refer to these as types of global protections.

As another variation, a reinsurance cover may be defined on a per event, or per occurrence of a claim, basis in lieu of the per risk basis that has been described so far. This approach is very handy to protect against, for example, natural catastrophes such as earthquakes or hurricanes where there may be many losses due to a common event. For example, a reinsurer’s obligation may be of the form \[ Y_{reinsurer} = \sum_{j \in \text{event}} \min[(X_j-u_{1,j})_+, u_{2,j}] . \] When combining several reinsurance features into a single contract, proportional arrangements such as quota share arrangements are easy to include. As an example, it is common for an insurer to have simultaneous quota share contracts on the same portfolio with different reinsurers. Many other variations are routinely used in practice.

Video: Section Summary

4.2 Modeling Dependence with Copulas

4.2.1 Copulas Defined

Copulas are widely used in insurance and many other fields to model the dependence among multivariate outcomes. A copula is a multivariate distribution function with uniform marginals. Specifically, let $\{V_1, \ldots, V_p\}$ be $p$ uniform random variables on $(0,1)$. Their joint distribution function \[ C(v_1, \ldots, v_p) = \Pr(V_1 \leq v_1, \ldots, V_p \leq v_p) \] is a copula. Of course, applications are based on more than just uniformly distributed data. Thus, consider arbitrary marginal distribution functions $F_1(\cdot)$,…,$F_p(\cdot)$. Then, one can define a multivariate distribution function $F$ using the copula such that \[\begin{equation} F(y_1, \ldots, y_p)= C[F_1(y_1), \ldots, F_p(y_p)]. \tag{4.3} \end{equation}\] Sklar (1959) showed the converse, that is, any multivariate distribution function can be written in the form of equation (4.3), that is, using a copula representation. Note on Notation: We use $V$ and $v$ for uniform random variables and their realizations in order to distinguish them from other terms, including utility functions $U$ and upper limits $u$.

As an example with $p=2$ variables, let us look to the copula due to Frank (1979), \[\begin{equation} C_F(v_1,v_2) = \frac{1}{\gamma} \log \left( 1+ \frac{ (\exp(\gamma v_1) -1)(\exp(\gamma v_2) -1)} {\exp(\gamma) -1} \right). \tag{4.4} \end{equation}\] This is a bivariate distribution function with its domain on the unit square $[0,1]^2.$ It is easy to see that $C_F(v_1,1) = v_1$. From this, one can argue that the marginals have a uniform (on $[0,1]$) distribution and so $C_F(\cdot,\cdot)$ is a copula. Further, one can interpret $\gamma$ to be a dependence parameter in that the extent of dependence is controlled by the parameter $\gamma$.

The copula due to Frank (1979) has a simple expression in equation (4.4) (at least simple relative to other copulas) and enjoys several desirable properties. However, it does not readily extend to multiple dimensions (a point of emphasis in this book). So, as an alternative, let us also introduce the normal, or Gaussian, copula. In two dimensions, this is given as \[\begin{equation} C_N(v_1,v_2) = \Phi_2\left[\Phi^{-1}(v_1), \Phi^{-1}(v_2) \right]. \tag{4.5} \end{equation}\] The expression in equation (4.5) appears more forbidding than Frank’s copula but is just as easy to evaluate. The symbol $\Phi(\cdot)$ represents the cumulative standard normal distribution and $\Phi^{-1}(\cdot)$ is the corresponding inverse function, or quantile. In R, these can be evaluated using the functions pnorm and qnorm, respectively. The symbol $\Phi_2(\cdot)$ represents a bivariate normal distribution function that, in R, can be evaluated using the function mvtnorm.

Because both the Frank and normal copulas are used extensively in applications, it is not surprising that they are both available as R functions (e.g., in the package copula, see examples that follow). So, users do not really need the mathematical expressions in equations (4.4) and (4.5). Nonetheless, it is helpful to have some familiarity with the mathematical underpinnings of the technique.

One important strength of the copula approach is evident from equation (4.3). We will be able to work with multiple risks, perhaps the first one being gamma distribution, the second having a Pareto distribution, the third having a normal distribution. Even though each marginal distribution may be very different from one another, one can link (or couple) them using a copula.

4.2.2 Copulas, Risk Retention, and Simulation

Copulas are well known to work in many arenas of scientific applications but how do they work in risk retention problems? To get some insights, consider the following example.

Example 4.2.1. Standard Deviation of an Excess of Loss Policy with Two Risks. Consider two risks:

That $X_1$ has a gamma distribution with mean 10000 and scale 5,000. The 95th percentile of $X_1$ is 23,719.
That $X_2$ has a Pareto distribution with mean 1000 and scale 2,000. The 95th percentile of $X_2$ is 3,429.

Their relationship is governed by a normal copula with dependence parameter $\rho_S = 0.30$.

The risk owner retains $S(u_1,u_2) = X_1 \wedge u_1 + X_2 \wedge u_2$ and calibrates uncertainty through \[ \begin{array}{ll} \mathrm{Var}[S(u_1,u_2)] & = \mathrm{E}[S(u_1,u_2)]^2 - [\mathrm{E} S(u_1,u_2)]^2\\ & = \mathrm{E}[(X_1 \wedge u_1)^2]+\mathrm{E}[(X_2 \wedge u_2)^2]+2\mathrm{E}[(X_1 \wedge u_1)(X_2 \wedge u_2)]\\ & \ \ \ \ \ - [\mathrm{E}(X_1 \wedge u_1)+\mathrm{E}(X_2 \wedge u_2)]^2 .\\ \end{array} \] As in Section 4.1.2, we utilize the relationships \[ \mathrm{E}(X \wedge u) = \int_0^u ~[1- F(x)]dx ~~~~ \text{and} ~~~~ \mathrm{E}(X \wedge u)^2 = 2\int_0^u ~x[1- F(x)]dx. \] These functions are easy to compute and, for example, are readily available in R through the package actuar. One can evaluate the expected cross-product of limited variables using \[\begin{equation} \begin{array}{rl} \mathrm{E} [(X_1 \wedge u_1)(X_2 \wedge u_2)] & = \int_0^{u_2} \int_0^{u_1} ~\Pr(X_1 >x_1, X_2> x_2) ~dx_1 dx_2 \\ & = \int_0^{u_2} \int_0^{u_1} ~\left[1 -F_1(x_1) - F_2(x_2) +F(x_1,x_2) \right]~dx_1 dx_2 .\\ \end{array} \tag{4.6} \end{equation}\]

$Under~the~Hood.$ Check the Limited Cross Product Expectation Equation (4.6)

Taking conditional expectations of the left-hand side yields,

\[ \mathrm{E} (X_1 \wedge u_1)(X_2 \wedge u_2) = \mathrm{E} \left\{ (X_1 \wedge u_1) \mathrm{E}_{X_1} (X_2 \wedge u_2) \right\} , \]

where

\[ \mathrm{E}_{X_1} (X_2 \wedge u_2) =\int_0^{u_2} ~[1- F(x_2|X_1)]dx_2 . \]

From this,

\[ \begin{array}{ll} \mathrm{E} (X_1 \wedge u_1)(X_2 \wedge u_2) &= \mathrm{E} \left\{ (X_1 \wedge u_1) \int_0^{u_2} ~(1- F(x_2|X_1))dx_2 \right\} \\ &= \int_0^{u_1} x_1 \int_0^{u_2} ~[1- F(x_2|x_1)]dx_2 ~f_1(x_1) dx_1 \\ &+ \int_{u_1}^{\infty} u_1 \int_0^{u_2} ~[1- F(x_2|x_1)]dx_2 ~f_1(x_1) dx_1 .\\ \end{array} \]

Because

\[ F(x_2|x_1) = \int_0^{x_2} ~f(z|x_1) dz = \int_0^{x_2} ~\frac{f(x_1,z)}{f_1(x_1)} dz \ \ \ \text{and} \ \ \ \frac{\partial}{\partial x_1} F(x_1,x_2) =\int_0^{x_2} ~f(x_1, z)dz . \]

we have

\[ f_1(x_1)(1- F(x_2|x_1)) =\frac{\partial}{\partial x_1} \left[F_1(x_1) -F(x_1,x_2) \right] . \]

With a change of integral,

\[ \begin{array}{ll} \int_{u_1}^{\infty} u_1 \int_0^{u_2} &\left\{(1- F(x_2|x_1))~f_1(x_1)\right\} dx_2 dx_1 \\ & = u_1 \int_0^{u_2}\int_{u_1}^{\infty} ~\left\{(1- F(x_2|x_1))~f_1(x_1)\right\} dx_1 dx_2 \\ &= u_1 \int_0^{u_2} \int_{u_1}^{\infty} ~\left\{\frac{\partial}{\partial x_1} \left[F_1(x_1) -F(x_1,x_2) \right]\right\} dx_1 dx_2 \\ &= u_1 \int_0^{u_2} ~\left[1-F_2(x_2)-(F_1(u_1) -F(u_1,x_2)) \right] dx_2 \\ &= u_1 ~\mathrm{E} (X_2 \wedge u_2) - u_1\int_0^{u_2} ~\left[F_1(u_1) -F(u_1,x_2) \right] dx_2 . \\ \end{array} \]

With a change of integral and integration by parts,

\[ {\small \begin{array}{ll} \int_0^{u_1} \int_0^{u_2} & x_1 (1- F(x_2|x_1))dx_2 ~f_1(x_1) dx_1 \\ & = \int_0^{u_2}\int_0^{u_1} ~x_1 \left\{(1- F(x_2|x_1))~f_1(x_1)\right\} dx_1 dx_2 \\ & = \int_0^{u_2} \left[ \int_0^{u_1} ~x_1 \left\{\frac{\partial}{\partial x_1} \left[F_1(x_1) -F(x_1,x_2) \right]\right\} dx_1 \right]dx_2 \\ & = \int_0^{u_2} \left[ ~x_1 \left[F_1(x_1) -F(x_1,x_2) \right]_0^{u_1} - \int_0^{u_1} ~\left[F_1(x_1) -F(x_1,x_2) \right]dx_1 \right]dx_2 \\ & = \int_0^{u_2} \left[ ~u_1 \left[F_1(u_1) -F(u_1,x_2) \right] - \int_0^{u_1} ~\left[F_1(x_1) -F(x_1,x_2) \right]dx_1 \right]dx_2 \\ \end{array} } \]

Summing, yields the result in equation (4.6).

\[ {\small \begin{array}{ll} & \mathrm{E} (X_1 \wedge u_1)(X_2 \wedge u_2) \\ & \ \ \ = u_1 ~\mathrm{E} (X_2 \wedge u_2) -\int_0^{u_2} \int_0^{u_1} ~\left[F_1(x_1) -F(x_1,x_2) \right]dx_1 dx_2 \\ & \ \ \ = ~u_1 ~\mathrm{E} (X_2 \wedge u_2) + ~u_2 ~\mathrm{E} (X_1 \wedge u_1) - ~ \int_0^{u_2} \int_0^{u_1} ~\left[1 -F(x_1,x_2) \right]dx_1 dx_2 \\ \end{array} } \]

Although the double integral in equation (4.6) can be readily evaluated for a single point $(u_1,u_2)$, this becomes burdensome as we go through many iterations seeking optimal values through iterative constrained optimization procedures beginning in the next section. (Chapter 5 will demonstrate this complexity.) A simpler approach is the following:

Using simulation, create a random realization of the bivariate uniform random variates $(V_{1r}, V_{2r})$. In the R package copula, one can do this with the function rCopula.
Use the inverse of the distribution function to create random realizations of the random variables, $X_{1r} = F_1^{-1}(V_{1r})$ and $X_{2r} = F_2^{-1}(V_{2r})$.
- For $F_1^{-1}$, in R use the function qgamma.
- For $F_2^{-1}$, in R use the function qpareto.
Create a random realization of the limited sum, $S_r(u_1,u_2) = X_{1r} \wedge u_1 + X_{2r} \wedge u_2$.
Repeat this for a large number, $R$, of replications. Summarize using the approximation \[ \widehat{Var}[S_R(u_1,u_2)] = \frac{1}{R} \sum_{r=1}^R \left[S_r(u_1,u_2)-\bar{S}_R(u_1,u_2)\right]^2, \] where $\bar{S}_R$ is the average value of the replicates $S_r(u_1,u_2)$.

R Code to Evaluate Variance

Figure 4.4 summarizes results. As anticipated, the uncertainty of retained risk increases as the upper limits increase.

R Code to Show the Figures

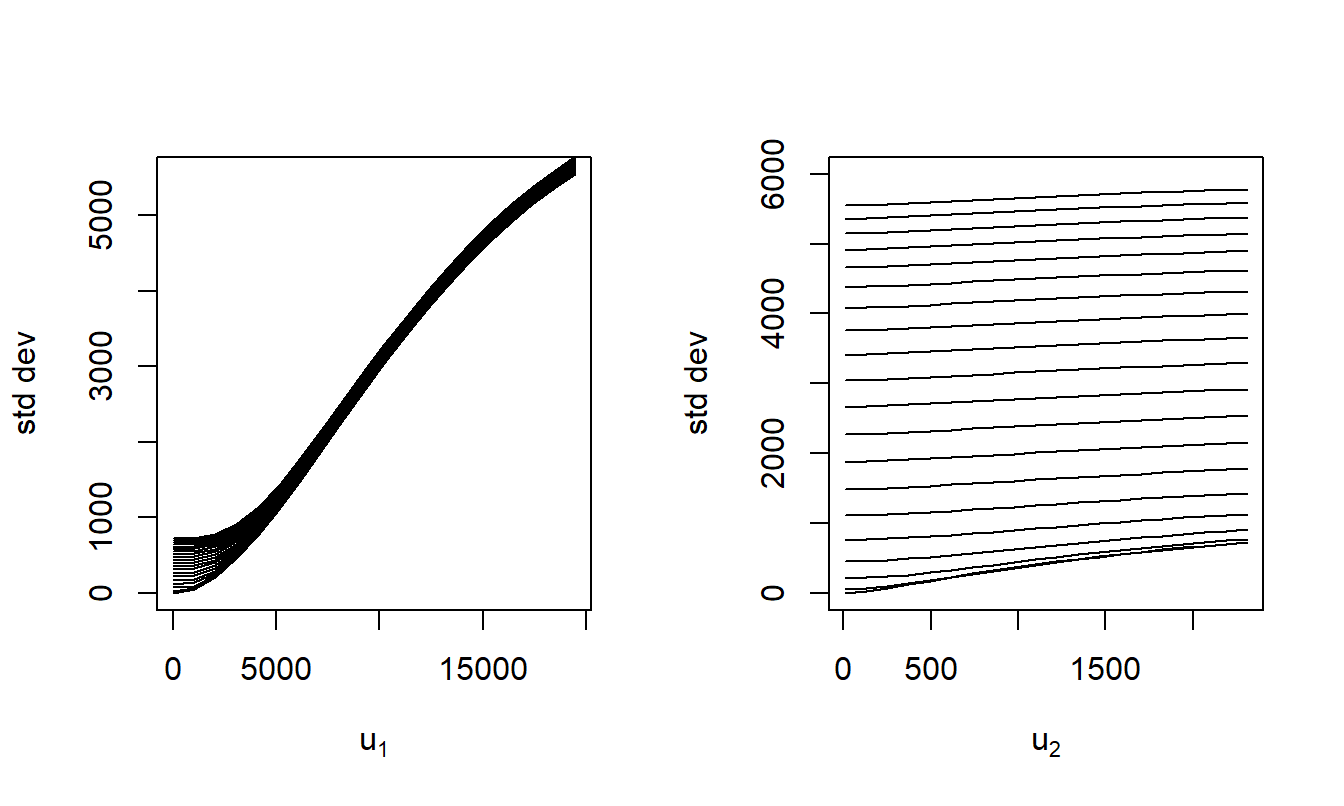
Standard Deviation of Retained Risk. The left panel show the standard deviation of the retained risk (its square, the variance, is the objective function) as a function of the first upper limit. Here, different lines represent different values of the second upper limit. The right panel compares the standard deviation to the second upper limit.

Figure 4.4: Standard Deviation of Retained Risk. The left panel show the standard deviation of the retained risk (its square, the variance, is the objective function) as a function of the first upper limit. Here, different lines represent different values of the second upper limit. The right panel compares the standard deviation to the second upper limit.

Video: Section Summary

4.3 Incorporating Dependence

Now return to the basic reinsurance treaties and let us see how they fare in the face of dependence. Let us start with a simple example to show how dependence affects risk measures. After this, one can then address the question as to how these optimal allocations change as the dependence changes. We develop this strategy first for quota share, then for excess of loss contracts.

4.3.1 Effects of Dependence on Risk Measures

It is not surprising that dependence affects our measures of uncertainty. In general, positive dependence leads to greater uncertainty, and hence larger values of risk measures. To be concrete, let us see how these general ideas work in a specific example.

Example 4.3.1. Effects of Dependence on Portfolio Summary Measures. Consider a portfolio management situation outlined in Exercise 4.1.1 that assumed that the property and liability risks are independent. Now, let us incorporate dependence by allowing the four lines of business to depend on one another through a Gaussian copula. For simplicity, assume a constant parameter equal 0.5 among the four lines.

Table 4.1 summarizes the results for the dependent portfolio in the lower three rows. For comparison, the top three rows provide results for the independence case. As anticipated, the mean losses are virtually identical when comparing the independent to dependent portfolios. The standard deviations (square root of our variance measure) for the dependent portfolio are larger for the reinsurer and in total. This larger uncertainty is also reflected in the values at risk at different levels of confidence.

Table 4.1: **Portfolio Expected Values, Standard Deviations, and Quantiles ($VaR_{\alpha}$)**
	Mean	Std Dev	$VaR_{0.90}$	$VaR_{0.95}$	$VaR_{0.99}$
Retained (Ind)	269	48	300	300	300
Reinsurer (Ind)	2333	3907	4487	6269	12644
Total (Ind)	2602	3909	4760	6541	12907
Retained (Dep)	269	48	300	300	300
Reinsurer (Dep)	2336	4067	4498	6283	12772
Total (Dep)	2605	4068	4770	6556	13052

R Code for the Table

# For the gamma distributions, use
alpha1 <- 2;      theta1 <- 100
alpha2 <- 2;      theta2 <- 200
# For the Pareto distributions, use
alpha3 <- 2;      theta3 <- 1000
alpha4 <- 3;      theta4 <- 2000
# Deductibles
d1     <- 100
d2     <- 200

# Simulate the risks
nSim <- 500000  #number of simulations
set.seed(2017) #set seed to reproduce work 
X1 <- rgamma(nSim,alpha1,scale = theta1)  
X2 <- rgamma(nSim,alpha2,scale = theta2)  
X3 <- actuar::rpareto(nSim,scale=theta3,shape=alpha3)
X4 <- actuar::rpareto(nSim,scale=theta4,shape=alpha4)
# Portfolio Risks
S             <- X1 + X2 + X3 + X4
Sretained     <- pmin(X1,d1) + pmin(X2,d2)
Sreinsurer    <- S - Sretained
OutMat        <- matrix(0, nrow = 6, ncol = 5)
OutMat[1:3,1] <- t(as.matrix(c(mean(Sretained),mean(Sreinsurer),mean(S))))
OutMat[1:3,2] <- t(as.matrix(c(sd(Sretained),sd(Sreinsurer),sd(S))))
OutMat[1,3:5] <- quantile(Sretained,  probs=c( 0.90, 0.95, 0.99))
OutMat[2,3:5] <- quantile(Sreinsurer, probs=c( 0.90, 0.95, 0.99))
OutMat[3,3:5] <- quantile(S        ,  probs=c( 0.90, 0.95, 0.99))

### Normal Copula ##
set.seed(2017)
parm <- c(0.5,0.5,0.5,0.5,0.5,0.5)*0
nc   <- copula::normalCopula(parm, dim = 4, dispstr = "un")
mcc  <- copula::mvdc(nc, margins = c("gamma", "gamma","paretoII","paretoII"), 
                     paramMargins = list(list(scale = theta1, shape=alpha1),
                                list(scale = theta2, shape=alpha2),
                                list(scale = theta3, shape=alpha3),
                                list(scale = theta4, shape=alpha4) ) )
X <- copula::rMvdc(nSim, mvdc = mcc)  # Another way to simulate
X1<-X[,1]
X2<-X[,2]
X3<-X[,3]
X4<-X[,4]

# Portfolio Risks
S            <- X1 + X2 + X3 + X4
Sretained   <- pmin(X1,d1) + pmin(X2,d2)
Sreinsurer  <- S - Sretained

OutMat[4:6,1] <- t(as.matrix(c(mean(Sretained),mean(Sreinsurer),mean(S))))
OutMat[4:6,2] <- t(as.matrix(c(sd(Sretained),sd(Sreinsurer),sd(S))))
OutMat[4,3:5] <- quantile(Sretained,  probs=c( 0.90, 0.95, 0.99))
OutMat[5,3:5] <- quantile(Sreinsurer, probs=c( 0.90, 0.95, 0.99))
OutMat[6,3:5] <- quantile(S        ,  probs=c( 0.90, 0.95, 0.99))

rownames(OutMat) <- c("Retained (Ind)", "Reinsurer (Ind)","Total (Ind)", 
                      "Retained (Dep)", "Reinsurer (Dep)","Total (Dep)") 
colnames(OutMat) <- c("Mean", "Std Dev","$VaR_{0.90}$", "$VaR_{0.95}$", "$VaR_{0.99}$")

TableGen1(TableData=OutMat,
         TextTitle='Portfolio Expected Values,
                    Standard Deviations, and Quantiles ($VaR_{\\alpha}$)',
         Align='r', Digits=0, ColumnSpec=1:5,
         BorderRight=1, ColWidth = ColWidth5,
         ColWidth0 = "4cm")

4.3.2 Quota Share

I now extend the discussion in Section 4.1.1 to include dependence.

For the quota share agreement, recall that the insurer’s portion of the portfolio risk is $Y_{retained} = \sum_{i=1}^p c_i X_i$ $= \mathbf{c}^{\prime} \mathbf{X}$. The objective is to find those values of $c_i$ that minimize $\mathrm{Var}(Y_{retained})$ subject to the budget constraint $\mathrm{E}(Y_{reinsurer}) = RTC_{max}$.

This is similar to the Markowitz asset allocation problem introduced in Section 3.4. At least in the asset allocation version, the problem is well known and so is the solution, details are in Exercise 4.4.1. Nonetheless, we give the solution here to provide a solid foundation so that we can use a similar approach later for more complicated problems. For the quota share version of the problem, define the Lagrangian \[ \begin{array}{ll} LA &= \mathrm{Var}(Y_{retained}) + LME~ [\mathrm{E}(Y_{reinsurer}) - RTC_{max}] \\ &= \mathbf{c}^{\prime} \boldsymbol \Sigma \mathbf{c} + LME~ [\mathrm{E}(\mathbf{X})^{\prime}(\mathbf{1}-\mathbf{c}) - RTC_{max}] . \end{array} \] Taking derivatives yields \[ \begin{array}{ll} \frac{\partial}{\partial \mathbf{c}}LA &= 2 \boldsymbol \Sigma \mathbf{c} - LME ~[\mathrm{E}(\mathbf{X})] = \mathbf{0}\\ \implies& \mathbf{c}^*= \frac{LME^*}{2} ~\boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X}) . \end{array} \] This is consistent with the case of independence in equation (4.1). From this, one can determine $LME^*$ as the solution of \[ \begin{array}{ll} &RTC_{max} = (\mathrm{E}~\mathbf{X} )^{\prime}[\mathbf{1}-\mathbf{c}^*] = (\mathrm{E}~\mathbf{X} )^{\prime}[\mathbf{1}-\frac{LME}{2}~ ~\boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X})] \\ \implies & LME^* =2\frac{(\mathrm{E}~\mathbf{X} )^{\prime}\mathbf{1}-RTC_{max}}{\mathrm{E}(\mathbf{X})^{\prime} ~\boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X})} ~~ . \end{array} \] For the quota share problem, the coinsurance parameters $c_j$ need not sum to one in contrast to the asset allocation problem in Exercise 4.4.1. However, it is common to require that these parameters be in the unit interval $[0,1]$. This can be formulated as a constrained optimization problem although the solution is not as tidy, see Exercise 10.1.

Example 4.3.2. Quota Share Example with Three Risks. This demonstration assumes that the third risk has the same distribution as the first. For the value of $RTC_{max}$, we use 4,200, which is 20% of the sum of expected losses. In this example, one can use association parameters and a Gaussian copula as inputs. One can then approximate the variance-covariance matrix $\boldsymbol \Sigma$ using simulation.

R Code For Quota Share Calculations

Table 4.2: **Quota Share Summary**
	Mean	Std Dev	Corr 1	Corr 2	Corr 3	c
Gamma1	10000	7071	1.0	-0.2	0.8	0.758
Pareto	1000	1732	-0.2	1.0	-0.3	0.378
Gamma2	10000	7071	0.8	-0.3	1.0	0.884

Table 4.2 summarizes results for the baseline case.

Now, repeat assuming zero correlations among risks to see the difference. Table 4.3 summarizes these results. There is a large difference in the retention parameters $\mathbf{c}$ when the dependence changes, particularly for the Pareto risk.

Table 4.3: **Quota Share Summary - with Zero Correlations**
	Mean	Std Dev	Corr 1	Corr 2	Corr 3	c
Gamma1	10000	7071	1	0	0	0.829
Pareto	1000	1732	0	1	0	0.076
Gamma2	10000	7071	0	0	1	0.843

Table 4.4 shows that one does not have to look that hard to find a negative coefficient associated with a risk. Although common in the investment world (shorting an asset), we have little interest in this possibility in insurance settings.

Table 4.4: **Quota Share Summary - with Positive Correlations**
	Mean	Std Dev	Corr 1	Corr 2	Corr 3	c
Gamma1	10000	7071	1.0	0.2	0.4	0.537
Pareto	1000	1732	0.2	1.0	0.8	-0.705
Gamma2	10000	7071	0.4	0.8	1.0	1.214

4.3.3 Excess of Loss

As in Section 4.1.2, for the excess of loss setting we consider $p$ risks $X_1, \ldots, X_p$ where each risk is subject to an upper limit, say, $u_i$. With this, the insurer retains $Y_{retained} =$ $\sum_{i=1}^p X_i \wedge u_i$ and the reinsurer is responsible for the excess, $Y_{reinsurer}=S - Y_{retained}$. The retention limits may vary by risk or may be the same for all risks, $u_i =u$, for all $i$.

What is the best choice of the excess of loss retention limits $u_i$? To formalize this question, we seek to find those values of $u_i$ that minimize $\mathrm{Var}(Y_{retained})$ subject to the constraint that $\mathrm{E}(Y_{reinsurer}) = RTC_{max}$. That is, subject to this budget constraint, the insurer wishes to minimize the uncertainty of the retained risks (as measured by the variance).

Section 4.4 will outline several approaches for solving this problem numerically. Let us see how one might do this using the root finding methods that will be described in Section 4.4.4. In part, we explore this now simply to demonstrate the difficulties associated with this approach. To implement this approach, assume that the budget constraint is binding. Further, one needs derivatives. So, start with the Lagrangian \[ LA(u_1, \ldots, u_p, LME) = \mathrm{Var}(Y_{retained}) + LME ~ [\mathrm{E}(Y_{reinsurer}) - RTC_{max}]. \] It is convenient to introduce an integrated tail function \[ \begin{array}{ll} IT_{ij}(a,b) &=\int_0^{b} ~\left\{1 -F_i(a) - F_j(z) +F_{ij}(a,z) \right\}~ dz \\ &=\int_0^{b} ~\Pr(X_i > a ,X_j > z)~ dz ,\\ \end{array} \] where $F_{ij}$ is the joint distribution function of the random variables $X_i$ and $X_j$. After some pleasant calculus, one can check that the partial derivatives are \[\begin{equation} \begin{array}{rl} \partial_{u_i} ~LA(u_1, \ldots, u_p, LME) &=2 \left[u_i - \sum_{j=1}^p ~\mathrm{E}(X_j \wedge u_j) - \frac{LME}{2} \right][1-F_i(u_i)] \\ &\ \ \ \ \ +2 \sum_{j \ne i} \left\{ IT_{ij}(u_i,u_j) \right\} , \\ \end{array} \tag{4.7} \end{equation}\] for $i=1, \ldots, p$, and \[\begin{equation} \partial_{LME} ~ LA(u_1, \ldots, u_p, LME) = \mathrm{E}(S) - \sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) - RTC_{max} . \tag{4.8} \end{equation}\]

$Under~the~Hood.$ Verification of Equation (4.7)

We start with the Lagrangian

\[ \begin{array}{ll} & LA(u_1, \ldots, u_p, LME) \\&= \mathrm{Var}(Y_{retained}) + LME ~[\mathrm{E}(Y_{reinsurer}) - RTC_{max}] .\\ \end{array} \]

From equation (4.6), we have

\[ \begin{array}{ll} &\partial_{u_1} \mathrm{E}\{(X_1 \wedge u_1)(X_2 \wedge u_2) \} \\ &=\partial_{u_1}\{\int_0^{u_2} \int_0^{u_1} ~\left[1 -F_1(x_1) - F_2(x_2) +F_{12}(x_1,x_2) \right]~dx_1 dx_2 \} \\ &=\int_0^{u_2} ~\left\{1 -F_1(u_1) - F_2(x_2) +F_{12}(u_1,x_2) \right\}~ dx_2 \\ & = IT_{12}(u_1,u_2),\\ \end{array} \]

where we define the asymmetric function

\[ \begin{array}{ll} IT_{12}(a,b) &=\int_0^{b} ~\left\{1 -F_1(a) - F_2(z) +F_{12}(a,z) \right\}~ dz \\ &=\int_0^{b} ~\Pr(X_1 > a ,X_2 > z)~ dz .\\ \end{array} \]

Now, taking the variance of retained risks yields

\[ \begin{array}{ll} & \partial_{u_1} \mathrm{Var}(Y_{retained}) \\ & =\partial_{u_1} \left\{\sum_{i,j} ~\mathrm{E}[(X_i \wedge u_i)(X_j \wedge u_j)] - \left[\sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) \right]^2 \right\}\\ &= \partial_{u_1} \mathrm{E}(X_1 \wedge u_1)^2 +2 \sum_{j \ne 1} \left\{ \partial_{u_1} ~\mathrm{E}(X_1 \wedge u_1)(X_j \wedge u_j) \right\}\\ & \ \ \ - 2\left[\sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) \right] \partial_{u_1}\mathrm{E}(X_1 \wedge u_1)\\ &= 2 u_1[1-F_1(u_1)] +2 \sum_{j \ne 1} \left\{ IT_{1j}(u_1,u_j) \right\} \\ & \ \ \ - 2\left[\sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) \right] [1-F_1(u_1)] \\ &= 2 \left[u_1 - \sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) \right][1-F_1(u_1)] +2 \sum_{j \ne 1} \left\{ IT_{1j}(u_1,u_j) \right\} \\ \end{array} \]

Now, taking the derivative of the Lagrangian yields

\[ \begin{array}{ll} & \partial_{u_1} LA(u_1, \ldots, u_p, LME) \\ &= \partial_{u_1} \mathrm{Var}(Y_{retained}) + \partial_{u_1} LME ~[\mathrm{E}(S)-\mathrm{E}(Y_{retained}) - RTC_{max}] \\ &= \partial_{u_1} \mathrm{Var}(Y_{retained}) -LME ~ \partial_{u_1} \mathrm{E}(Y_{retained}) \\ &=2 \left[u_1 - \sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) \right][1-F_1(u_1)] +2 \sum_{j \ne 1} \left\{ IT_{1j}(u_1,u_j) \right\} \\ &\ \ \ \ - LME~\partial_{u_1} \mathrm{E}(X_1 \wedge u_1) \\ &=2 \left[u_1 - \sum_{i=1}^p ~\mathrm{E}(X_i \wedge u_i) - \frac{LME}{2} \right][1-F_1(u_1)] +2 \sum_{j \ne 1} \left\{ IT_{1j}(u_1,u_j) \right\} .\\ \end{array} \]

This verifies equation (4.7). Equation (4.8) is immediate from the budget constraint.

Setting these derivatives to zero, there are $p+1$ equations and $p+1$ unknowns which can be solved numerically. Numerical solutions require starting values; solutions can sometimes be sensitive to the choice of starting values. Fortunately, for this problem, one can look to the case of independence developed in Section 4.1.2 for starting values.

Special Case - Independent Risks. It is convenient to first define an integrated distribution function $H_{1i}(x) = \int_0^{x} F_i(z) dz$. With this notation, it can be shown we may determine $LME^*$ as the solution of the equation \[ \mathrm{E}(S) - RTC_{max} = \sum_{i=1}^p \left\{ H_{1i}^{-1}\left(\frac{LME}{2}\right) - \frac{LME}{2} \right\} .\\ \] With a value of $LME^*$, one can calculate the optimal retention limits using $u_i^* = H_{1i}^{-1}(\frac{LME^*}{2})$.

$Under~the~Hood.$ Independence Case Details

Example 4.3.3. Optimal Upper Limits with Excess of Loss for Three Dependent Risks. Now return to the same set of marginal distributions as in the quota share Example 4.3.2. Also as in this example, let $RTC_{max} = 4,200$, which is 20% of the sum of expected losses. For the Gaussian copula parameters, we use \[ \boldsymbol \rho = \left( \begin{array}{ccc} 1 & \rho_{12} & \rho_{13}\\ \rho_{12} & 1& \rho_{23}\\ \rho_{13} & \rho_{23}& 1\\ \end{array} \right) \] with $\rho_{12} =$ 0.95, $\rho_{13} =$ 0, and $\rho_{23} =$ 0. Note that the rho parameters are based on the copula, not (Pearson) correlations among the risks.

R Code For Excess of Loss Dependent Risks Calculations

param      <- c(0.95, 0.0, 0.0)
risk2shape <- 3
risk2scale <- 2000
ELoss.XL  <- ERisk1fun()+ERisk2fun()+ERisk3fun()
RCOSTmax  <- 0.2*ELoss.XL
K         <- ELoss.XL - RCOSTmax
paramM    <- c(1.1*ERisk1fun(),1.2*ERisk2fun(),1.1*ERisk3fun())
H11       <- function(u){integrate(F1, lower = 0, upper = u)$value }
H12       <- function(u){integrate(F2, lower = 0, upper = u)$value }
H13       <- function(u){integrate(F3, lower = 0, upper = u)$value }
H1        <- function(u){u-H11(u)}
H2        <- function(u){u-H12(u)}
H3        <- function(u){u-H13(u)}
# Inverse Functions
H11inv <- function(lambda){H11star <- function(x){H11(x)-lambda}  
          return(uniroot(H11star, lower = 0, upper = UpRangeRisk1)$root)}
H12inv <- function(lambda){H12star <- function(x){H12(x)-lambda}  
          return(uniroot(H12star, lower = 0, upper = UpRangeRisk2)$root)}
H13inv <- function(lambda){H13star <- function(x){H13(x)-lambda}  
          return(uniroot(H13star, lower = 0, upper = UpRangeRisk3)$root)}
IndExLoss <- function(lambda){
             H11inv(lambda/2) + H12inv(lambda/2)  + 
             H13inv(lambda/2) - 3*lambda/2 - K
             }
IndExLoss <- function(lambda){
             H11inv(lambda/2) + H12inv(lambda/2)  + 
             H13inv(lambda/2) - 3*lambda/2 - (ELoss.XL-RCOSTmax)
             }
lambda.opt <- uniroot(IndExLoss, lower = 0, upper = 9e5)$root
#  Gradient Functions
g.1 <- function(MParms){
       M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
       return(2*H11(M1) - lambda)
       }
g.2 <- function(MParms){
       M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
       return(2*H12(M2) - lambda)
       }
g.3 <- function(MParms){
       M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
       return(2*H13(M3) - lambda)
       }
g.4 <- function(MParms){
       M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
       return(H1(M1)+H2(M2)+H3(M3) - (ELoss.XL-RCOSTmax) )
       }

model <- function(MParms) {
         c(F1=g.1(MParms),F2=g.2(MParms),
         F3=g.3(MParms),F4=g.4(MParms))}
XL    <- rootSolve::multiroot(f = model, start = c(1000,1000,1000,1000))
sol.ind.params <- round(XL$root, digits=0)

######################################################################
# Now try Dependent case
#param <- c(-0.2, 0.3, -0.3)
#param <- c(0,0,0)
norm.cop   <- copula::normalCopula(param=param, dim = 3,'dispstr' ="un") 
norm.cop12 <- copula::normalCopula(param=as.numeric(param[1]), dim = 2) 
norm.cop13 <- copula::normalCopula(param=as.numeric(param[2]), dim = 2) 
norm.cop23 <- copula::normalCopula(param=as.numeric(param[3]), dim = 2) 

F.MX <- function(arg){
  MParms <- arg[1:4];i <- arg[5]; j<- arg[6]
  M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
  if ( (i==1)*(j==2) + (i==2)*(j==1) ) {norm.cop<- norm.cop12}
  if ( (i==1)*(j==3) + (i==3)*(j==1) ) {norm.cop<- norm.cop13}
  if ( (i==2)*(j==3) + (i==3)*(j==2) ) {norm.cop<- norm.cop23}  
  FiMi <- F1(M1)*(i==1) + F2(M2)*(i==2) + F3(M3)*(i==3)  
  JointF_MX <- function(z){
    F1jz <- F1(z)*(j==1) + F2(z)*(j==2) + F3(z)*(j==3) 
    return(FiMi-pCopula(c(FiMi,F1jz), norm.cop))
    }
  VecJointF_MX <- Vectorize(JointF_MX)
  return(integrate(VecJointF_MX, lower = 0, upper = MParms[j])$value) 
  }
#  Gradient Functions
g.1.dep <- function(MParms){
  M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
  eqeval <- 2*( ELoss.XL - RCOSTmax-H1(M1) ) - 
    2*( F.MX(c(MParms,1,2)) + F.MX(c(MParms,1,3)) ) +
    ( 2*M1-2*(ELoss.XL-RCOSTmax)-lambda)*(1-F1(M1) )
  return(eqeval)
  }
g.2.dep <- function(MParms){
  M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
  eqeval <- 2*(ELoss.XL-RCOSTmax-H2(M2)) - 
            2*(F.MX(c(MParms,2,1))+F.MX(c(MParms,2,3))) +
            (2*M2-2*(ELoss.XL-RCOSTmax)-lambda)*(1-F2(M2))
  return(eqeval)
  }
g.3.dep <- function(MParms){
  M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
  eqeval <- 2*(ELoss.XL-RCOSTmax-H3(M3)) - 
            2*(F.MX(c(MParms,3,1))+F.MX(c(MParms,3,2))) +
            (2*M3-2*(ELoss.XL-RCOSTmax)-lambda)*(1-F3(M3))
  return(eqeval)
  }
g.4 <- function(MParms){
  M1 <- MParms[1];M2 <- MParms[2];M3 <- MParms[3];lambda <- MParms[4]
  eqeval <- H1(M1)+H2(M2)+H3(M3) - (ELoss.XL-RCOSTmax )
  return(eqeval)
  }
model <- function(MParms) {c(F1=g.1.dep(MParms),F2=g.2.dep(MParms),
                             F3=g.3.dep(MParms),F4=g.4(MParms))}
XL.dep <- multiroot(f = model, start = sol.ind.params)
sol.dep.params <- round(XL.dep$root, digits=0)
ERiskVec <- c(ERisk1fun(),ERisk2fun(),ERisk3fun(), "")
ind.Frac <- c(round(c(F1(sol.ind.params[1]),F2(sol.ind.params[2]),
                      F3(sol.ind.params[3])), digits=3), "")
dep.Frac <- c(round(c(F1(sol.dep.params[1]),F2(sol.dep.params[2]),
                      F3(sol.dep.params[3])), digits=3), "")
ExLossDepOut <- cbind(ERiskVec,sol.ind.params,
                      ind.Frac,sol.dep.params,dep.Frac)
rownames(ExLossDepOut) <- c("Gamma1", "Pareto", "Gamma2","LME")
colnames(ExLossDepOut) <- c("Mean", "Optimal Ind u","Ind u Prop", 
                            "Optimal Dep u","Dep u Prop")
save(sol.ind.params, sol.dep.params, ExLossDepOut, 
     file="../ChapTablesData/Chap4/Example433.Rdata")

Table 4.5: **Excess of Loss Dependent Risks Summary**
	Mean	Optimal Ind $u^*$	Ind $u^*$ Prop	Optimal Dep $u^*$	Dep $u^*$ Prop
Gamma1	10000	11806	0.683	11938	0.689
Pareto	1000	4775	0.974	1214	0.759
Gamma2	10000	11806	0.683	12673	0.72
LME		7725		8942

Table 4.5 shows the optimal upper limits under both models of independence and dependence. Comparing these results, it appears that there can be important differences between the optimal limits based on the dependence.

In addition, another way to view these is to think about their position in the marginal distribution. Specifically, the optimal retention parameters can also be expressed as proportions for the corresponding marginal distribution functions. So, for example, for the best choice of $u_1$ under the model of independence on the original scale is 11,806; this is the 68.3 percentile of this gamma distribution. Extending this logic to the second row, the upper limits are 97.4 percentile for the independence model versus 75.9 percentile for the dependence model. Thus, when viewed as a percentile or on the original scale, 4,775 versus 1,214, it appears that the dependence assumption can influence the optimal upper limits.

Video: Section Summary

4.4 Numerical Optimization

Recall the general constrained optimization problem in Display (3.9) from Section 3.3.4, \[ \boxed{ \begin{array}{cccr} {\small \text{minimize}_{{\bf z}}} & f_0({\bf z}) & \\ {\small \text{subject to}} & f_{con,j}({\bf z}) \le 0 & j \in CON_{in} & \ \ \ \ \ \ \ \ \ \ \\\ & f_{con,j}({\bf z}) = 0 & j \in CON_{eq} . \end{array} } \] Here, $f_0(\cdot)$ is the objective function that we wish to minimize subject to conditions on the constraints $f_{con,j}(\cdot)$ in the inequality ($CON_{in}$) and equality ($CON_{eq}$) sets.

4.4.1 Convex Optimization

In today’s computing environment, the optimization problem described in Display (3.9) is relatively straightforward if we can identify the problem as convex. There are some minor variations in the definition of convex optimization in the literature; I use the conditions put forward in Boyd and Vandenberghe (2004). Specifically, let us require that the objective function $f_0({\bf z})$ and inequality constraints $f_{con,j}({\bf z}), j \in CON_{in}$ are convex and that the equality constraints $f_{con,j}({\bf z}), j \in CON_{eq}$ are affine. By affine (or linear), I mean that one can write $f_{con,j}({\bf z}) = {\bf A} {\bf z} - {\bf b}$ for some matrix ${\bf A}$ and vector ${\bf b}$. (For a refresher, refer to the Appendix Section 3.6.3 for definitions of convexity and other terms.)

Classical problems based on proportional (e.g., quota sharing) rules with the variance as a measure of risk are typically convex. As an example, consider the quota sharing problem introduced in Section 4.1.1.1. The quota share coefficients are the parameters of interest and so ${\bf z} = \bf c$. The variance of the portfolio risk, $f_0({\bf z}) = \mathrm{Var}({\bf z}^{\prime} \mathbf{X})$ $= {\bf z}^{\prime} \boldsymbol \Sigma{\bf z}$, is the objective function to be minimized. This is quadratic in the parameters and hence typically convex. In the same way, the risk transfer condition can be seen to be linear in the parameters. Moreover, it will be straightforward to include parameter constraints of the form $c_i = z_i \ge 0$ and $c_i = z_i \le 1$ as these are linear and hence also convex. Recall that Section 4.3.2 described this problem in more detail.

For convex problems, there are many algorithms that are computationally efficient and that fare remarkably well even when the number of decision variables (the dimension of ${\bf z}$) is large. To illustrate this in our demonstrations, we use the R package CVXR; see Exercise 4.5.5. Moreover, as emphasized by Boyd and Vandenberghe (2004), local solutions to convex problems are also global solutions, a property that is not generally available for constrained optimization problems. Because of this property, many convex algorithms do not even require starting values.

Special Case: Asset Allocations

Asset allocations, summarized in Section 3.4, can be cast as a convex optimization problem. In addition, mathematically the asset allocation problem is similar to the quota share problem described in Section 4.3.2. Naturally, the practices are very different; the former considers allocation concerns of investors whereas the latter is about diversifying liabilities that is typically only done by insurers and major companies. A common simplifying feature of both problems is that the decision variables, $c_1, \ldots, c_p$, are linear in the risks. This means that the problem is convex in many situations. In this section, I expand the discussion and use the expected shortfall $ES$ as our risk measure.

To see the convexity of the problem, the approach is to define an expanded version of the expected shortfall function, \[ \begin{array}{ll} ES1(z_0,\mathbf{c}) &= z_0 + \frac{1}{1-\alpha} \left\{\mathrm{E}[\mathbf{c}'\mathbf{X}] -\mathrm{E}[\mathbf{c}'\mathbf{X} \wedge z_0]\right\}\\ &= z_0 + \frac{1}{1-\alpha} \mathrm{E}[\mathbf{c}'\mathbf{X} - z_0]_+ .\\ \end{array} \tag{4.9} \] For fixed values of $\mathbf{c}$, it is easy to check that the solution of the unconstrained minimization problem is the quantile. Moreover, the minimum value is the expected shortfall. This point will be developed in more detail in Section 7.2.2.

Moreover, we verify below that the function $ES1(z_0, \mathbf{c})$ is convex in the decision variables $z_0$ and $\mathbf{c}$. Because the minimum of a convex function is also convex (see, for example, Boyd and Vandenberghe (2004), Section 3.2.5), this means that the $ES$ function is convex.

$Under~the~Hood.$ Show the Verification of the Convexity

Earlier in Display (3.13), we wrote the asset allocation problem as minimizing the portfolio variance subject to constraints on the mean return. Now, we extend this by using the expected shortfall as our risk measure. Specifically, we consider \[\begin{equation} \boxed{ \begin{array}{lcc} {\small \text{minimize}}_{z_0, \mathbf{c}} & ES1(z_0, \mathbf{c}) & \\ {\small \text{subject to}} & \mathbf{c}^{\prime} ~\mathrm{E}(\mathbf{R}) \ge Req_0 .\\ \end{array} } \tag{4.10} \end{equation}\]

Example 4.4.1. Optimizing a Portfolio of Insurance Stock Returns. This is a continuation of Example 1.3.1 and Example 3.4.1. We are now ready to compute the optimal portfolio specified in Display (4.10) with the CVXR package.

As in Example 3.4.1, we determine optimal allocations using the training data. With these allocations, various summary measures are computed. Then, the optimal allocations are used on the test data and several summary measures are determined.

Table 4.6 summarizes performance for both the training and test samples. For comparison purposes, the performance measures summarized earlier in Example 3.4.1 are also included.

R Code to ES Portfolios

Table 4.6: **Portfolio Performance Measures, with $ES$**
	Train Ann Return	Train Std Dev	Train Sharpe (Rf=0)	Test Ann Return	Test Std Dev	Test Sharpe (Rf=0)
MinVar	0.164	0.119	1.378	0.168	0.143	1.178
Markowitz	0.203	0.126	1.614	0.166	0.143	1.160
Equal	0.173	0.130	1.329	0.155	0.142	1.093
ES-$\alpha = 0.95$	0.173	0.120	1.436	0.158	0.144	1.099
ES-$\alpha = 0.99$	0.181	0.128	1.412	0.155	0.152	1.020

Another way of presenting the performance of the differing portfolios is to track their performance over time. In Figure 4.5, we can see that all portfolios behave similarly over the test period.

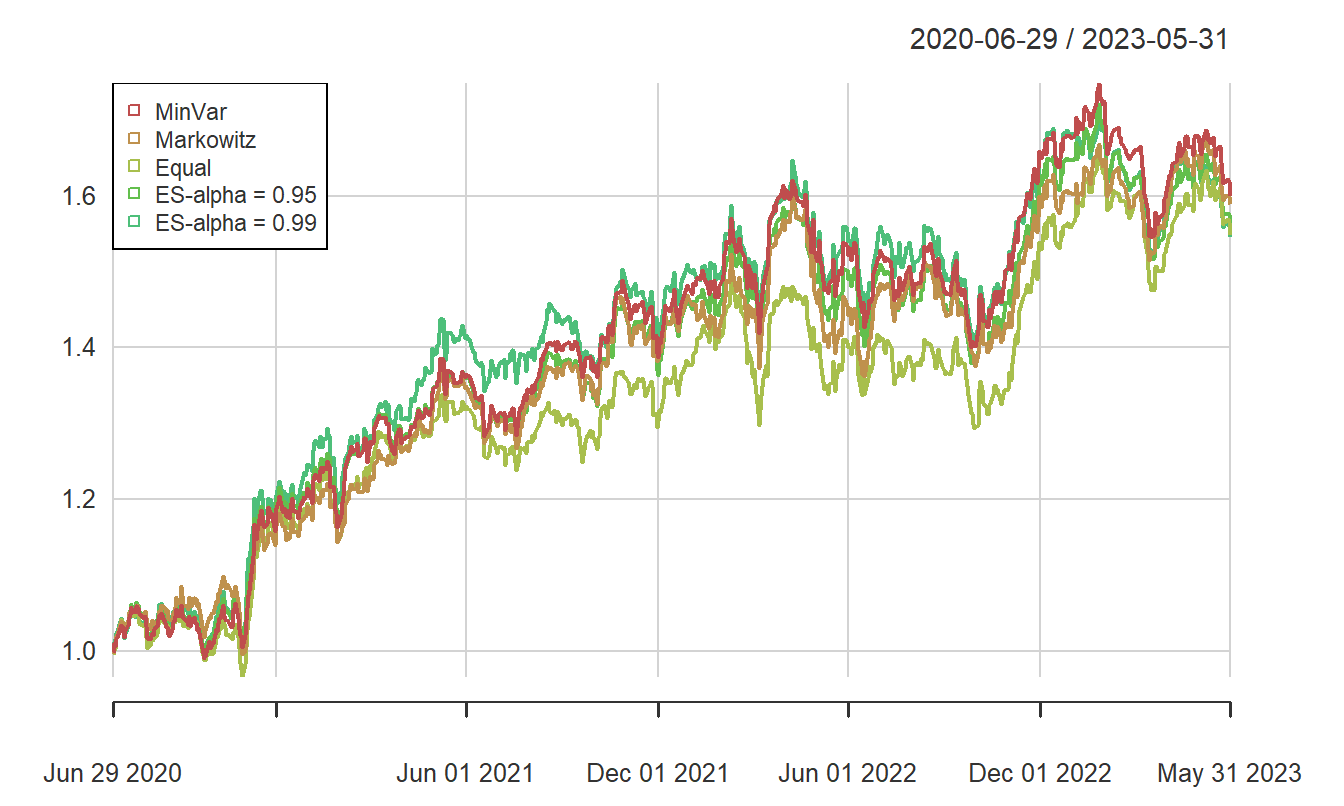
$Cumulative Portfolio Returns (Test Sample), with $ES$$

Figure 4.5: Cumulative Portfolio Returns (Test Sample), with $ES$

As emphasized in Example 3.4.1, one cannot conclude too much from these results. Practicing analysts will use this approach while conducting more extensive testing by varying the training period, the test period, and the sample of stocks (risks) selected. In addition, many of the constraints on allocations introduced in Section 3.4.2

will come into play (note that these allocation constraints are linear and so can readily be incorporated into the convex optimization problem). Readers are invited to experiment with the code to determine their own optimal portfolios.

4.4.2 Constrained Optimization Without Coding Derivatives

Many risk retention problems cannot be classified as convex and so we need a more general approach. For some problems, one only needs to code the objective and constraint functions and use these specifications in a numerical optimization program. Many modern programs now have the ability to calculate approximate derivatives using finite difference methods and use these approximations in lieu of analytical expressions for the derivatives. For many problems, this approach is much simpler for the user and often works well particularly when there are small numbers of decision variables and constraints. Nonetheless, for some problems, they can take much longer for convergence to optimal solutions when compared to methods using analytical derivatives. Further, they can be sensitive to algorithmic parameters such as starting values. I show how to use this approach in R using the function auglag from the package alabama.

However, in applied risk management problems even the evaluation of objective and constraint functions can be difficult. As seen in Example 4.2.1, this difficulty can be addressed using simulation as a method of approximating these functions. Virtually all numerical methods exhibit deviations from true values when evaluating a solution and simulation is certainly no exception. A strength of the simulation approach is that the approximation error can be reduced simply by increasing the number of simulated replicates. So, if the analyst is satisfied with a result based on the analysis of a simulated trial, then accuracy can be increased by replicating the simulated trial with a larger number of replicates. Let us see how the simulation approach is valuable in the following example.

Example 4.4.2. Constrained Optimization for Excess of Loss with Two Risks. Let us continue from Example 4.2.1. The risk owner retains $S(u_1,u_2) = X_1 \wedge u_1 + X_2 \wedge u_2$ and desires to minimize $f_0(u_1,u_2) = \mathrm{Var}[S(u_1,u_2)]$. This is constrained by the budget requirement $f_{con,1}(u_1,u_2) = RTC(u_1,u_2) - RTC_{max}\le 0$ and constraints on the parameters $f_{con,2}(u_1,u_2) =-u_1 \le 0$ and $f_{con,3}(u_1,u_2) =-u_2 \le 0$. For simplicity, we use a fair risk transfer cost $RTC(u_1,u_2) = \mathrm{E} [S(\infty,\infty)] - \mathrm{E}[S(u_1,u_2)]$. We use simulation to evaluate the objective function but not the risk transfer cost which is easy to evaluate.

R Code to Evaluate Constraint Functions

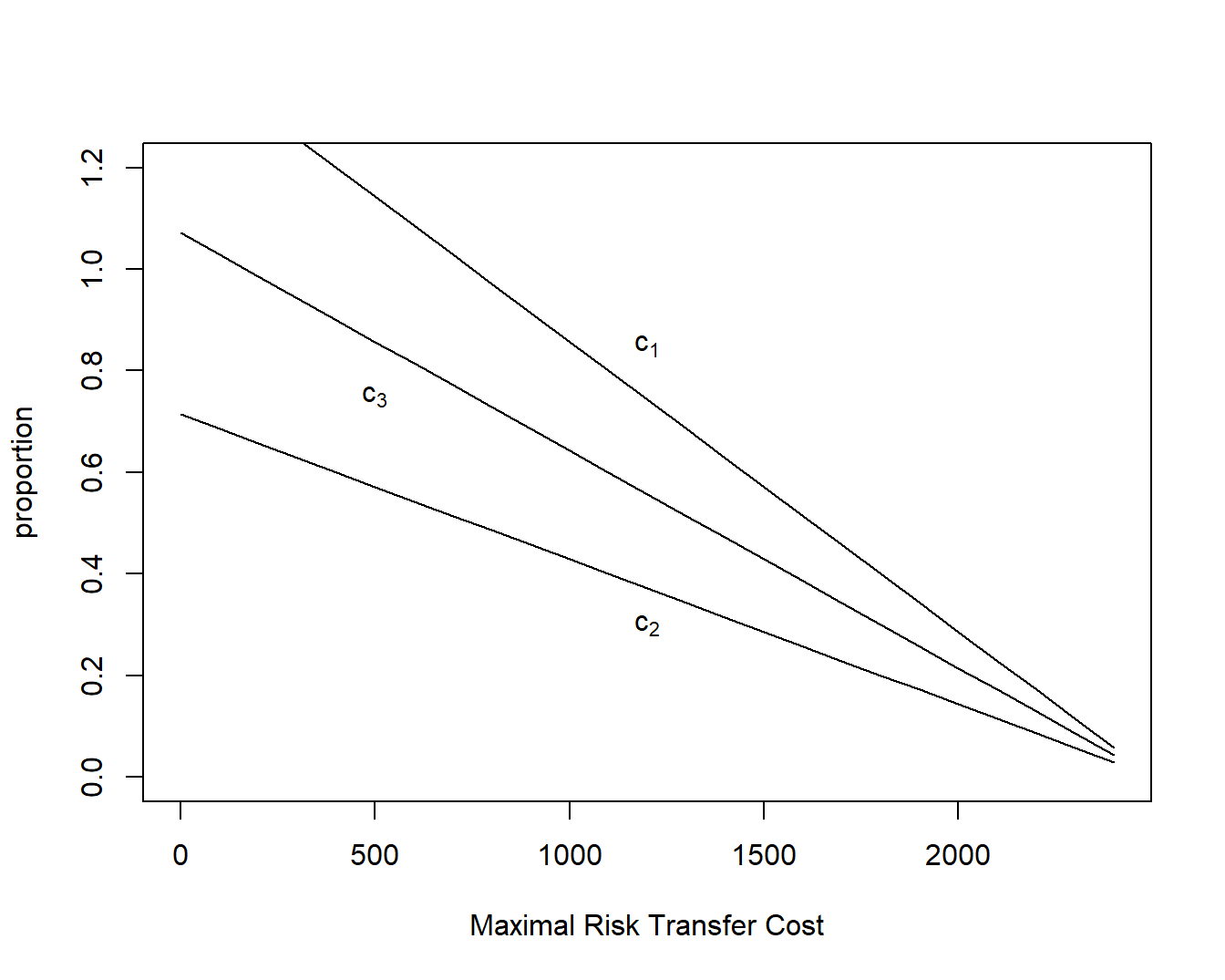
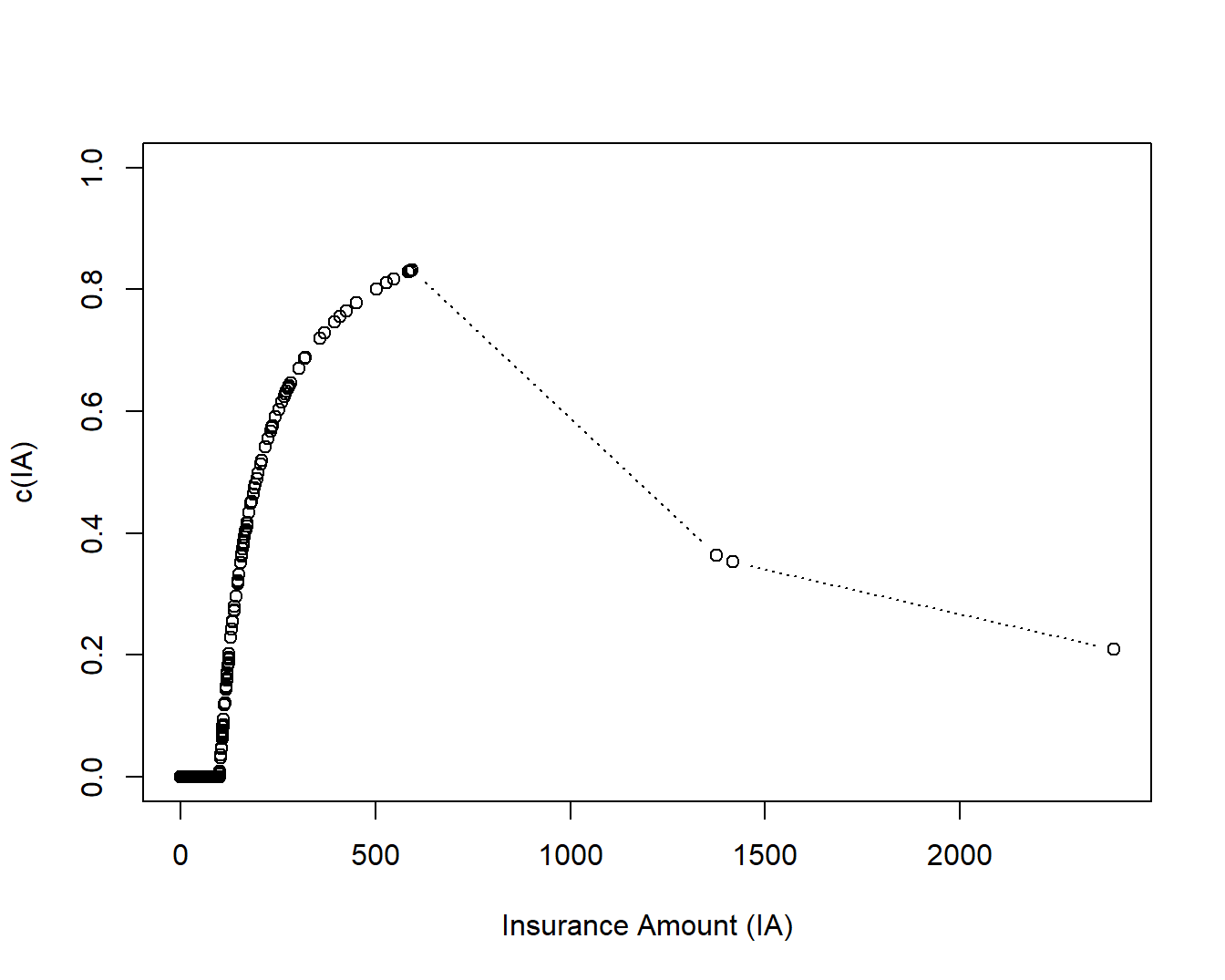
Recall from the earlier Example 4.2.1, Figure 4.4 showed the standard deviation of retained risks as a function of each upper limit. Figure 4.6 supplements this by showing the risk transfer cost $RTC$ as a function of each upper limit. As anticipated, the risk transfer cost $RTC$ decreases as each upper limit increases. The right-hand panel of Figure 4.6 demonstrates the trade-off between the risk transfer cost and the uncertainty of retained risk.

R Code to Show the Figures

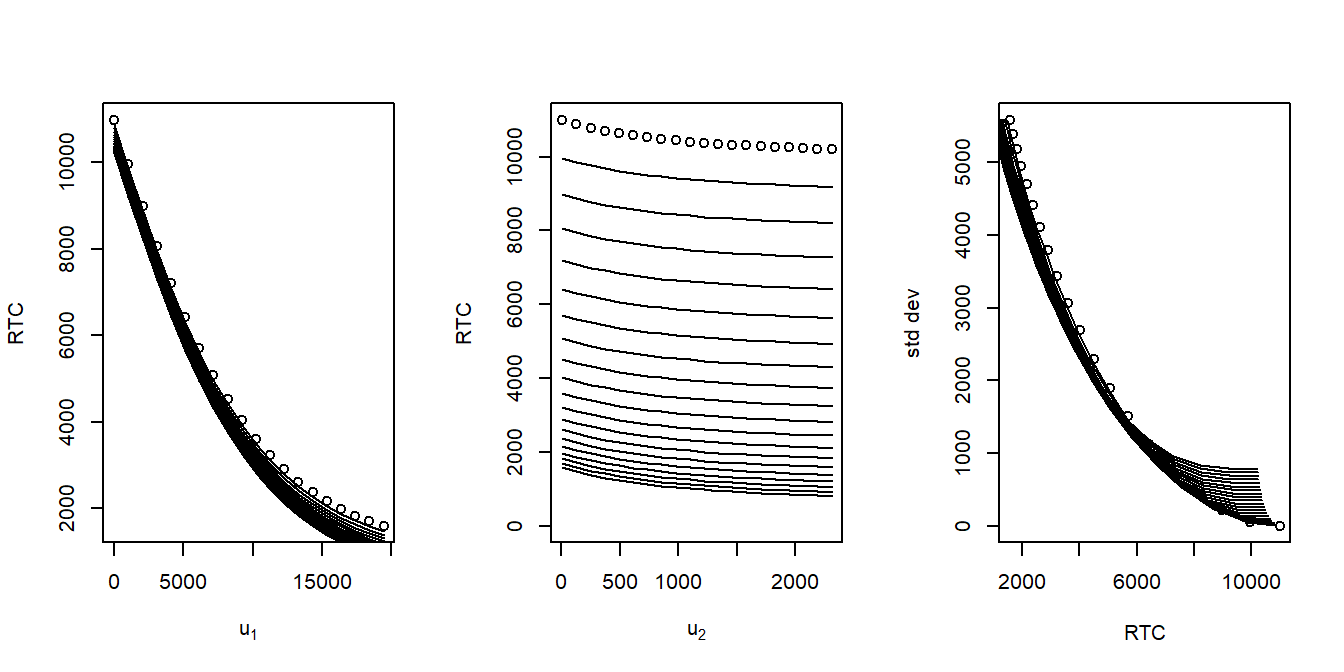
$Excess of Loss Parameters and Objective and Constraint Functions. The left panel shows the $RTC$ as a function of the first upper limit, with different lines representing different values of the second upper limit. The middle panel shows it as a function of the second upper limit, with different lines representing different values of the first upper limit. The right panel compares the $RTC$ to the standard deviation.$

Figure 4.6: Excess of Loss Parameters and Objective and Constraint Functions. The left panel shows the $RTC$ as a function of the first upper limit, with different lines representing different values of the second upper limit. The middle panel shows it as a function of the second upper limit, with different lines representing different values of the first upper limit. The right panel compares the $RTC$ to the standard deviation.

With these objective and constraint functions, one can then solve the constrained optimization problem that is demonstrated in the associated code. This is done for a specific value of $RTC_{max}$, which is then varied. This shows how the solution changes as the maximal risk transfer cost changes. Figure 4.7 summarizes results. Here, we see that as $RTC_{max}$ increases, the optimal upper limits decrease, as does the uncertainty of retained risk.

R Code for Optimization without Derivatives

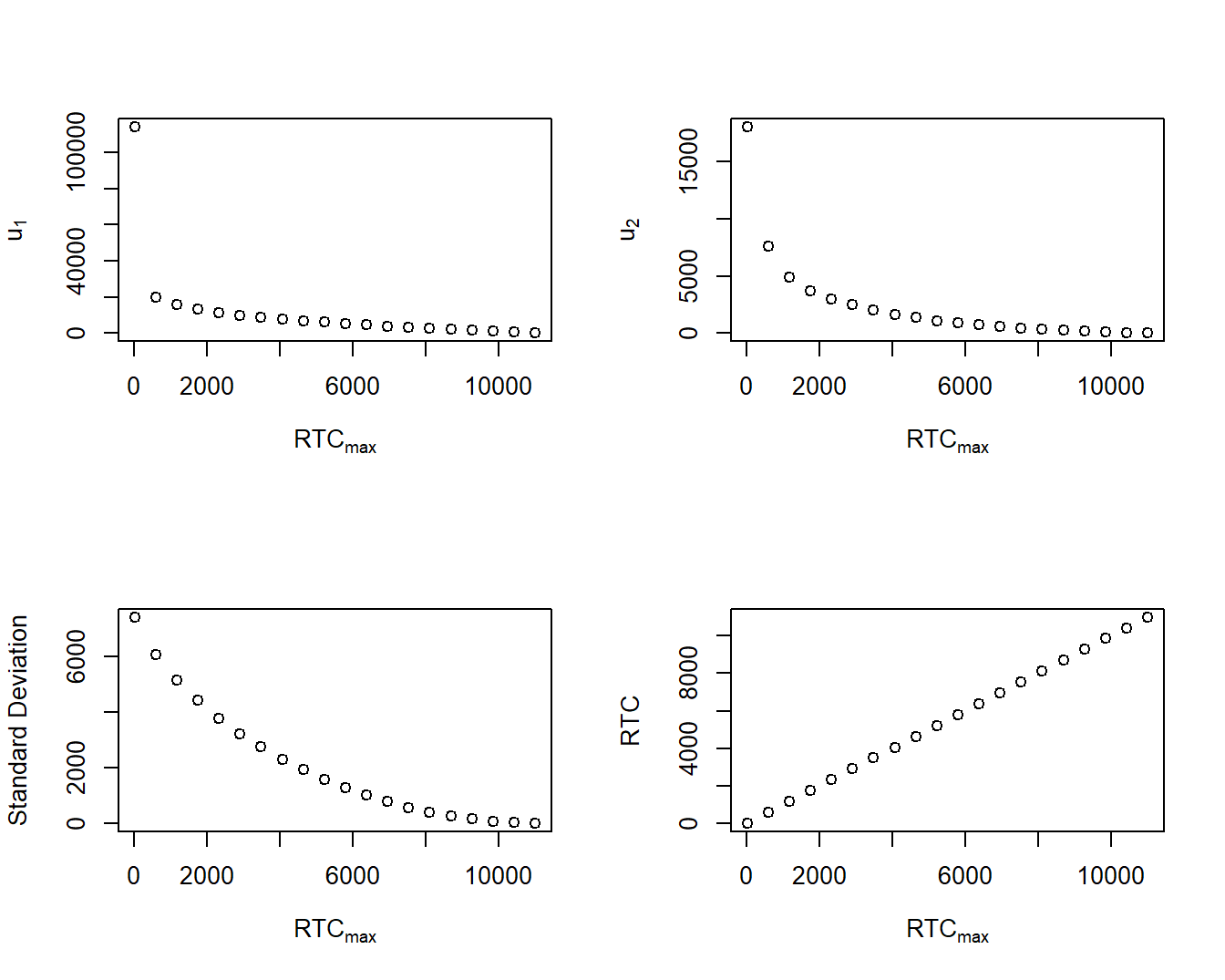
$Optimization Results as a Function of $RTC_{max}$. The upper left panel shows the optimal first upper limit as a function of the maximal risk transfer cost, $RTC_{max}$. The upper right panel gives the same information for the second upper limit. The lower left panel shows the best value of the standard deviation of retained risks as a function of the $RTC_{max}$. The lower right panel shows that the constraint is binding at each optimum.$

Figure 4.7: Optimization Results as a Function of $RTC_{max}$. The upper left panel shows the optimal first upper limit as a function of the maximal risk transfer cost, $RTC_{max}$. The upper right panel gives the same information for the second upper limit. The lower left panel shows the best value of the standard deviation of retained risks as a function of the $RTC_{max}$. The lower right panel shows that the constraint is binding at each optimum.

4.4.3 Constrained Optimization with Coding Derivatives

Another approach is to use a numerical optimization program that allows one to include derivatives of objective and constraint functions. This approach requires more upfront effort for the analyst, since you have to derive and code the derivatives, but often provides more stable and robust results. However, as seen in the following example, even developing the derivatives can be difficult.

Example 4.4.2. Excess of Loss with Two Risks – Continued. The derivatives of the constraint functions are relatively straightforward. We have \[ \begin{array}{ll} \partial_{u_j} f_{con,1}(u_1,u_2) & = \partial_{u_j} \left\{ \mathrm{E} (S(\infty,\infty)) - \mathrm{E}(S(u_1,u_2)) -RTC_{max} \right\} \\ & = -\partial_{u_j} \left\{ \mathrm{E}(X_1\wedge u_1 )+ \mathrm{E}(X_2\wedge u_2)\right\} \\ & = -\left\{ 1- F_j(u_j)\right\} , \end{array} \] as well as \[ \begin{array}{ll} \partial_{u_1} f_{con,2}(u_1,u_2) =\partial_{u_1} (-u_1) = -1, & \partial_{u_2} f_{con,2}(u_1,u_2) =\partial_{u_2} (-u_1) = ~~~0, \\ \partial_{u_1} f_{con,3}(u_1,u_2) =\partial_{u_1} (-u_2) = ~~~0, & \partial_{u_2} f_{con,3}(u_1,u_2) =\partial_{u_2} (-u_2) = -1 . \\ \end{array} \] For the objective function, a partial derivative can be shown to be \[\begin{equation} \begin{array}{ll} \partial_{u_1} f_0(u_1,u_2) & = \partial_{u_1} \mathrm{Var}[S(u_1,u_2)] \\ & = 2 \left\{ (u_1+u_2-\mathrm{E} [S(u_1,u_2)])[1-F_1(u_1)] \right. \\ & \left. \ \ \ \ -\int_0^{u_2} ~\left[ F_2(x_2) -F(u_1,x_2) \right]dx_2 \right\} .\\ \end{array} \tag{4.11} \end{equation}\] The result for the other gradient, $\partial_{u_2} f_0(u_1,u_2)$, follows in the same way, simply switch the indices.

$Under~the~Hood.$ Show the Verification of the Derivative of the Objective Function

The associated R code for constrained maximization with derivatives uses the auglag function. This code provides essentially the same results as those without derivatives and so the output is suppressed (the exception is when $RTC_{max}$ is very small and there are numerical difficulties). For this example, it takes longer than the results without derivatives. This is because the numerical evaluation of the integral above required for each step of the minimization process. The code numerically evaluates the partial derivatives of the constraints and objective function yet uses a simulation approximation for the objective function. This is because the calculation of the variance requires double integration which can be computationally intensive when done as part of an iterative optimization procedure.

R Code to Optimization with Derivatives

library(alabama)
F1 <- function(x){pgamma(q=x,shape = risk1shape, scale = risk1scale)}
F2 <- function(x){actuar::ppareto(q=x,shape = risk2shape, scale = risk2scale)}

f0.grad1 <- function(u1,u2){
  Fu1.x2 <- function(x2){F2(x2)-pCopula(c(F1(u1),F2(x2)), norm.cop)}
  Fu1.x2.vec <- Vectorize(Fu1.x2)
  H11 <- function(u2){integrate(Fu1.x2.vec, lower = 0, upper = u2)$value }
  part <- u1+u2 - (actuar::levgamma(limit = u1, shape = risk1shape, 
                                    scale = risk1scale) + 
            actuar::levpareto(limit = u2,shape = risk2shape, 
                              scale = risk2scale))
  partial1 <- 2*(part * (1-F1(u1))  - H11(u2))
  return(partial1)
  }
f0.grad2 <- function(u1,u2){
  Fx1.u2 <- function(x1){F1(x1)-pCopula(c(F1(x1),F2(u2)), norm.cop)}
  Fx1.u2.vec <- Vectorize(Fx1.u2)
  H22 <- function(u1){integrate(Fx1.u2.vec , lower = 0, upper = u1)$value }
  part <- u1+u2 - 
    (actuar::levgamma(limit = u1, shape = risk1shape, scale = risk1scale) + 
     actuar::levpareto(limit = u2,shape = risk2shape,scale = risk2scale))
  partial2 <- 2*( part * (1-F2(u2))  - H22(u1) )
  return(partial2)
}
  gr <- function(par) {gr <- NA
  gr[1] <- f0.grad1(u1=par[1],u2=par[2])
# non-negativity constraint on first parameter    
  gr[2] <- f0.grad2(u1=par[1],u2=par[2])  
  return(gr)
  }

OptMat <- matrix(0,20,4) 
RTCVec <- seq(10, RTCUpper, length.out=20)
for (kindex in 1:length(RTCVec)) {
  f1.ala <- function(par){-(f1in(u1=par[1],u2=par[2])-RTCVec[kindex])}
  hin <- function(par) {h <- NA
    h[1] <- f1.ala(par)
    h[2] <- par[1]  # non-negativity constraint on first parameter
    h[3] <- par[2]
    return(h)}
  var.opt <- alabama::auglag(par=starter, # initial value
            fn=f0.ala,           # objective function
            gr=gr,               # gradient of the objective function
            hin=hin,             # inequality constraint
            control.outer=list(method="nlminb",trace=FALSE))
  OptMat[kindex,1:2] <- var.opt$par
  OptMat[kindex,3]   <- f0(var.opt$par[1],var.opt$par[2])
  OptMat[kindex,4]   <- f1in(var.opt$par[1],var.opt$par[2])
}
round(OptMat, digits=2)

4.4.4 Root-Finding Methods (with Derivatives)

With derivatives developed and coded, we can also employ a more basic approach. Simply take the derivatives of the Lagrangian, set these equal to zero, and solve a system of equations using a root-finding algorithm. That is, the beauty of the Lagrangian approach is that it turns a constrained optimization problem into an unconstrained one. And, we know from calculus, for many smooth problems, you simply take a derivative of the function and solve for zeros to get its critical values. The limitation of this approach, mentioned earlier, is the working assumption that the constraints are active, or binding, at the optimum.

This approach can be implemented numerically in R using the function multiroot from the rootSolve package, see the associated R code. Like any root-finding algorithm, this function only finds critical values (of which there may be many) and it is up to the analyst to ensure that they minimize the objective function over the entire feasible region. Further, the function requires starting values which, when varied, can lead to different critical values.

Example 4.4.2. Excess of Loss with Two Risks – Continued. The associated R code shows how to solve the problem using root finding methods. As before, because the results are similar to those from other approaches, the findings are not displayed.

R Code for Optimization Using Root-Finding Methods Example 4.4.2

library(rootSolve)

param      <- c(0.95, 0.0, 0.0)
norm.cop   <- copula::normalCopula(param=param, dim = 3,'dispstr' ="un") 
norm.cop12 <- copula::normalCopula(param=as.numeric(param[1]), dim = 2) 
f0.grad1   <- function(u1,u2,LM){
  Fu1.x2   <- function(x2){F2(x2)-pCopula(c(F1(u1),F2(x2)), norm.cop12)}
  Fu1.x2.vec <- Vectorize(Fu1.x2)
  H11      <- function(u2){integrate(Fu1.x2.vec, lower = 0, 
                                upper = u2)$value }
  part     <- u1+u2 - 
    (actuar::levgamma(limit = u1,  shape = risk1shape, scale = risk1scale) + 
     actuar::levpareto(limit = u2, shape = risk2shape, scale = risk2scale) )
  partial1 <- 2*(part * (1-F1(u1))  - H11(u2))
  return(partial1)
}

f0.grad1(u1=start[1],u2=start[2],LM=start[3])
f0.grad2 <- function(u1,u2,LM){
  Fx1.u2 <- function(x1){F1(x1)-pCopula(c(F1(x1),F2(u2)), norm.cop12)}
  Fx1.u2.vec <- Vectorize(Fx1.u2)
  H22 <- function(u1){integrate(Fx1.u2.vec , lower = 0,
                                upper = u1)$value }
  part <- u1+u2 - 
    (actuar::levgamma(limit = u1,  shape = risk1shape, scale = risk1scale) + 
     actuar::levpareto(limit = u2, shape = risk2shape,scale = risk2scale) )
  partial2 <- 2*(part * (1-F2(u2))  - H22(u1) )
  return(partial2)
  }

f1in.grad1 <- function(u1,u2,LM){-1*(1-F1(u1))}
f1in.grad2 <- function(u1,u2,LM){-1*(1-F2(u2))}
LA.grad1 <- function(u1,u2,LM){f0.grad1(u1,u2) + LM*f1in.grad1(u1,u2) }
LA.grad2 <- function(u1,u2,LM){f0.grad2(u1,u2) + LM*f1in.grad2(u1,u2) }

RTCUpper <- actuar::mgamma(order=1,  shape = risk1shape, scale = risk1scale) +
            actuar::mpareto(order=1, shape = risk2shape, scale = risk2scale) - 1
#  Start at mean values
starter = c(actuar::mgamma(order=1, shape = risk1shape, scale = risk1scale),
            actuar::mpareto(order=1, shape = risk2shape, scale = risk2scale) )

OptMatMulti <- matrix(0,20,6) 
RTCVec <- seq(10, RTCUpper, length.out=20)
for (kindex in 1:(length(RTCVec)-1)) {
 LA.grad3 <- function(u1,u2,LM) {f1in(u1,u2)-RTCVec[kindex]} 
 model <- function(MParms) {
   c(F1=LA.grad1(MParms[1],MParms[2],MParms[3]),
     F2=LA.grad2(MParms[1],MParms[2],MParms[3]),
     F3=LA.grad3(MParms[1],MParms[2],MParms[3]))}
 starterA <- starter/kindex
 model(start)
 LA.grad1(start[1],start[2],start[3])
 
ss <- multiroot(f = model, start = c(starterA,10000))
  OptMatMulti[kindex,1:3] <- ss$root
  OptMatMulti[kindex,4] <- f0(ss$root[1],ss$root[2])
  OptMatMulti[kindex,5] <- f1in(ss$root[1],ss$root[2])
  OptMatMulti[kindex,6] <- RTCVec[kindex]
}
colnames(OptMatMulti) <- c("u1","u2","LME", "f0", "f1in", "RTCmax")

round(OptMatMulti,digits = 2)

As another example of root-finding methods, you may wish to revisit the code in Example 4.3.3.

For analysts who wish to take a deeper dive into the intricacies of optimization problems in R, visit CRAN Task View: Optimization and Mathematical Programming. Among many other packages and approaches, this page has further links to three packages that focus on variations of the Lagrange method:

The package alabama provides an implementation of the augmented Lagrange multiplier method for solving nonlinear optimization problems with nonlinear equality and inequality constraints. The acronym stands for Augmented Lagrangian Adaptive Barrier Minimization Algorithm. This is the primary package used in this book.
The package nloptr provides access to various nonlinear optimization algorithms, including the augmented Lagrangian approach for nonlinear constraints.
The package Rsolnp also provides an implementation of the augmented Lagrange multiplier method for solving problems with equality and inequality constraints.

Video: Section Summary

4.5 Risk Exchanges

We have focused on a risk transfer defined to be the change of possession of an uncertain obligation, a risk, from one party to another in exchange for (certain) monetary compensation. This definition includes commercial insurance as well as many other mechanisms. For example, you might be the firm risk manager seeking to transfer risks due to unforeseen events that could damage the company’s property, financial health due to cyber events, and the well-being of the workforce due to accidents at the work facility. Corporate insurance is one way to transfer these potential liabilities but there are other possibilities, including self-insurance, utilizing a captive insurer, participation in a pool or group, insurance from a governmental entity, and other alternative risk transfer mechanisms. Section 6.2 will provide more detail on these alternatives. Although our primary focus is on insurance as a motivation for risk transfer, we aim to develop frameworks that are sufficiently general to handle other mechanisms as well.

Risk owners seek ways to offload some or all of their risk. Instead of simply ceding a portion of the risk, it is helpful to think about a general framework of exchanging risks. Specifically, we consider $n$ exchange participants known as agents. These agents may be risk owners, such as a firm or an individual, or they may be another party, such as an insurer or a pool. For example, an agent may be a reinsurer that brings no risk to the exchange but agrees to take on risks in exchange for a fee. Associated with each agent, say the ith one, is a set of p risks $\mathbf{X}_i = (X_{i1}, \ldots, X_{ip})$. A risk may be a (degenerate) random variable that has no uncertainty, such as cash.

When terms of a risk exchange have been agreed upon, a set of rules or functions $g_i$ is established, such that \[\begin{equation} \mathbf{Y}_i = g_i(\mathbf{X}_1, \ldots, \mathbf{X}_n), \ \ \ i=1, \ldots, n , \tag{4.12} \end{equation}\] defines the collection of risks of the ith agent after the exchange has taken place (but before the random variables have been realized). The goal of the risk exchange, also known as the risk-sharing, literature is to establish guidance for suitable choices of the rules $g_i$. For example, one basic principle in selecting the rules is to ensure that $\sum_{i=1}^n \mathbf{Y}_i = \sum_{i=1}^n \mathbf{X}_i$. This ensures that the sum of risks from all risk owners is equal before and after the exchange. In financial transactions, this principle is known as “clearing the market” and so clearing the exchange seems appropriate here.

Another fundamental goal is to achieve an improvement in the risk position for all parties. That is, the measure of uncertainty for the ith party after the exchange should not be larger than prior to the exchange. The reasoning is that if a party’s uncertainty increases due to the exchange, that party will not enter into the exchange.

In addition to these basic goals, there is another desirable principle known as Pareto optimality. An exchange is said to be Pareto-optimal if there is no other exchange that is strictly better. This principle, as with the risk improvement principle, depends on the type of risk measure used to quantify uncertainty, as well as the application area. Section 4.5.2 provides additional discussion on Pareto optimality. In the following three subsections, we provide some guidance based on separate strands of the actuarial literature. In the appendix Section 4.6.4, we describe an alternative approach for determining risk exchanges based on quantile risk measures such as $RVaR$.

4.5.1 Linear Exchanges

We now know that the risk exchange literature likely began with the work of De Finetti (1940); Seal (1969) provides a detailed description of its early history up to its publication date. Based on this long history, we adopt the structure put forth in Feng, Liu, and Taylor (2023).

Similar to most approaches, let us focus on only a single type of risk, so $p=1$. If cash is required to equate a risk-sharing agreement, one regards it as a “side payment.” In this section, we use variance as a measure of risk and, consistent with the early literature, emphasize proportional risk-sharing agreements.

Consider $n$ agents who have risks $X_1, \ldots, X_n$ to be shared among them. In the special case where all risks have the same distribution, it is desirable to share risks equally. That is, the share for agent i after the exchange is $Y_i = (X_1 + \cdots + X_n)/n$, the average. When the risks are independent, the uncertainty after the exchange $\text{Var}(Y_i)= \text{Var}(X_i)/n$ is much lower than prior to the exchange.

In general, risks do not have the same distribution nor are they independent. To handle this more complex situation, this subsection considers linear exchanges, or sharing rules, where risks are combined in an additive fashion and the proportion of each risk is set as part of the sharing rule. Specifically, define $c_{ij}$ to be the proportion of the $j$th risk that agent $i$ takes on after a risk-sharing agreement. In sum, the $i$th agent has responsibility for $Y_i = c_{i1}X_1 + \cdots + c_{in} X_n$, a random linear combination of losses. This can be summarized for all agents as: \[ \mathbf{Y} = \left( \begin{array}{c}Y_1 \\ \vdots \\Y_n \end{array} \right)= \left( \begin{array}{ccc}c_{11} &\cdots& c_{1n} \\ \vdots &\ddots &\vdots \\c_{n1} &\cdots &c_{nn} \end{array} \right) \left( \begin{array}{c}X_1 \\ \vdots \\X_n \end{array} \right) = \mathbf{C}\mathbf{X} . \] Several conditions potentially apply: \[\begin{equation} \boxed{ \begin{array}{cc} \mathbf{C}' {\bf 1}= {\bf 1} & \text{clearing the exchange} \\ \mathbf{C} \boldsymbol \mu = \boldsymbol \mu & \text{no profits}\\ 0 \le c_{ij} \le 1 & \text{no short/long selling} \\ \mathrm{Var} (Y_i) \le \mathrm{Var} (X_i) & \text{risk improvement} \end{array} } . \tag{4.13} \end{equation}\] The first condition, “clearing the exchange,” ensures that ${\bf 1' X} = {\bf 1}' {\bf C X} = {\bf 1' Y}$, so that the sum of risks before the exchange equals the sum of risks after the exchange, for any realization of the random vector $\mathbf{X}$. The second condition on the means ($\mathrm{E} ({\bf X}) = \boldsymbol \mu$) implies that this is a non-profit arrangement; that is, no agent can expect to make profit (so that $\mathrm{E} ({\bf Y}) = \mathrm{E} ({\bf X})$). The third condition excludes “short selling” (and “long” positions) as is common in financial investment transactions. An agent may not take a negative position nor more than 100% of a risk. The fourth condition is about improving a risk position; no agent will be worse off by participating in the risk-sharing agreement.

There are many choices of the matrix $\mathbf{C}$ that satisfy the conditions in Display (4.13). The identity matrix is certainly one, ensuring that the set of feasible parameters is not empty. To obtain a unique set of parameters, we focus on minimizing $\sum_i \mathrm{Var} (Y_i)$ over choices of $\mathbf{C}$ subject to the conditions in Display (4.13). Here, one can interpret $\sum_{i=1}^n \mathrm{Var}(Y_i)$ to be a “system variance.”

As is common for optimization problems, with only equality constraints one can obtain closed-form expressions for the solutions. This approach is outlined in Exercise 4.5.2 and Exercise 4.5.3. More generally (including inequality constraints), this is a convex programming problem that can be readily solved numerically. Specifically, it is a quadratic program, and so fast solvers are available (see, for example, Boyd and Vandenberghe (2004), Section 4.4). Fast solvers mean that it can be easy to optimize large dimensional problems. As an illustration, Exercise 4.5.3 outlines a strategy for $n=50$ agents (that works in about 4 minutes). Nonetheless, to start, first consider the following example.

Example 4.5.1. Linear Sharing Among Three Agents. Assume that $n=3$ and the mean vector and variance-covariance matrix are given as \[ \boldsymbol \mu = \left(\begin{array}{rrr}20 \\ 2.5 \\ 10 \end{array}\right) \ \ \ \ \ \ \text{and} \ \ \ \ \ \ \ \boldsymbol \Sigma = \left(\begin{array}{rrr} 10 & -4 & -1 \\ -4 & 8 & 1 \\ -1 & 1 & 1\\ \end{array}\right) . \] Prior to the exchange, the sum of all variances is $\sum_{i=1}^n \mathrm{Var}(X_i) =$ $10 + 8 + 1 = 19$. We then determine values of the coefficient matrix $\bf C$ that minimizes the system variance after the exchange, $\sum_{i=1}^n \mathrm{Var}(Y_i)$, subject to a sequence of constraints. The results are summarized in Tables 4.7 and Table 4.8 based on the associated R code.

R Code for Example 4.5.1

library(CVXR)
num.row     <- 3
ones.vec    <- as.vector(rep(1,num.row))
ones.mat    <- matrix (rep(1,num.row^2),nrow = num.row)
X.sigma     <- matrix(c(10, -4 , -1 , -4 , 8 , 1, -1 ,  1 , 1), nrow = num.row)
X.sigma.inv <- solve(X.sigma)
mu = as.vector(c( 20, 2.5, 10))
Results.mat <- matrix(0,4,5)
Results.mat[1:3,1] <- diag(X.sigma)
Results.mat[4,1]   <- sum(Results.mat[1:3,1])

## Exchange Clearing 
C.mat       <- Variable(3,3)
objective   <- quad_form(t(C.mat[1,]), X.sigma) + 
               quad_form(t(C.mat[2,]), X.sigma) + quad_form(t(C.mat[3,]), X.sigma)
constraints <- list(t(C.mat) %*% ones.vec == ones.vec)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)

C.opt.1     <- result$getValue(C.mat)
Summarize.Result <-function(Condnum,C.opt){
  Y.sigma <- C.opt %*% X.sigma %*% t(C.opt)
  Results.mat[1:3,Condnum+1] <- diag(Y.sigma)
  Results.mat[4,Condnum+1] <- sum(Results.mat[1:3,Condnum+1])
  return(Results.mat)
  }
Results.mat <- Summarize.Result(Condnum=1, C.opt=C.opt.1)

##  Exchange Clearing  and the No Profits Conditions
C.mat <- Variable(3,3)

objective    <- quad_form(t(C.mat[1,]), X.sigma) + quad_form(t(C.mat[2,]), X.sigma) +
                quad_form(t(C.mat[3,]), X.sigma)
constraints  <- list(t(C.mat) %*% ones.vec == ones.vec, C.mat %*% mu == mu)
prob         <- Problem(Minimize(objective), constraints)
result       <- solve(prob)

C.opt.2      <- result$getValue(C.mat)
Results.mat  <- Summarize.Result(Condnum=2,C.opt=C.opt.2)

## Add Limits
C.mat        <- Variable(3,3)
objective    <- quad_form(t(C.mat[1,]), X.sigma) + quad_form(t(C.mat[2,]), X.sigma) +
                quad_form(t(C.mat[3,]), X.sigma) 
constraints  <- list(t(C.mat) %*% ones.vec == ones.vec, 
                     C.mat %*% mu == mu, C.mat >= 0, C.mat <= 1)
prob         <- Problem(Minimize(objective), constraints)
result       <- solve(prob)
C.opt.3      <- result$getValue(C.mat)
Results.mat  <- Summarize.Result(Condnum=3,C.opt=C.opt.3)

## Add  Risk Improvement
C.mat        <- Variable(3,3)
objective    <- quad_form(t(C.mat[1,]), X.sigma) + quad_form(t(C.mat[2,]), X.sigma) +
                quad_form(t(C.mat[3,]), X.sigma) 
constraints  <- list(t(C.mat) %*% ones.vec == ones.vec, 
                   C.mat %*% mu == mu, C.mat >= 0, C.mat <= 1,
                   quad_form(t(C.mat[1,]), X.sigma) <= X.sigma[1,1],
                   quad_form(t(C.mat[2,]), X.sigma) <= X.sigma[2,2],
                   quad_form(t(C.mat[3,]), X.sigma) <= X.sigma[3,3])
prob         <- Problem(Minimize(objective), constraints)
result       <- solve(prob)
C.opt.4      <- result$getValue(C.mat)
Results.mat  <- Summarize.Result(Condnum=4,C.opt=C.opt.4)

# Check equality constraints
# t(C.opt.4) %*% ones.vec
# C.opt.4 %*% mu

# Check short selling
C.opt.3.mat  <- cbind(C.opt.1[,3],C.opt.2[,3],C.opt.3[,3],C.opt.4[,3])

rownames(Results.mat) <- c("Agent 1", "Agent 2", "Agent 3","Total")
colnames(Results.mat) <- c("Original",  "Clear Exchange", 
                           "No Profits","Short Sell", "Risk Improvement")

TableGen1(TableData=Results.mat, 
         TextTitle='Risk-Sharing Model Variances', 
         Align='rrrrr', Digits=4, ColumnSpec=1:5,
         BorderRight=1 )

Table 4.7 shows the impact of the exchange on the uncertainty measure for each agent. To illustrate, for Agent 1, the original (prior to the exchange) variance is $\mathrm{Var}(X_1)=10$. After imposing on the clearing exchange condition, Agent 1’s variance is $\mathrm{Var}(Y_1)=1.2222$. If instead one does the optimization problem with the clear exchange and the no profits condition, Agent 1’s variance is $\mathrm{Var}(Y_1)=2.6281$. Repeating, with the constraints clear exchange, no profits, and short sell, Agent 1’s variance is $\mathrm{Var}(Y_1)=2.8881$. Finally, with all four constraints, Agent 1’s variance is $\mathrm{Var}(Y_1)=3.3164$. The bottom row provides the sum of variances for all three agents. After the exchange, we see that the system variance increases as more constraints are imposed as one would expect. Nonetheless, all four options provide a smaller system variance than the original set-up. This illustrates the benefits of diversification.

It is also interesting to observe the uncertainty measure for Agent 3. From the third row of the table, we see that this agent’s variance actually increases under the first three exchanges. It is only when we specifically impose the risk improvement condition is this agent at least no worse off.

Table 4.7: **Risk-Sharing Model Variances**
	Original	Clear Exchange	No Profits	Short Sell	Risk Improvement
Agent 1	10	1.2222	2.6281	2.8881	3.3164
Agent 2	8	1.2222	0.6695	0.3415	0.4148
Agent 3	1	1.2222	1.1359	1.3959	1.0000
Total	19	3.6667	4.4335	4.6256	4.7312

Table 4.8 provides more details about the optimal coefficients. Each optimization procedure yields nine coefficients, three for each risk. The table shows only those for Risk 3. First note that each column sums to one, as required under the clearing the exchange condition. Also observe the negative coefficient in the No Profits column. This corresponds to an optimization problem before we explicitly introduce the short sell condition, indicating the importance of this condition. In fact, from the Short Sell column we see that the lower bound is a binding constraint for some coefficients.

Table 4.8: **Risk 3 Coefficients**
	Clear Exchange	No Profits	Short Sell	Risk Improvement
To Agent 1	0.3333	0.9286	0.8247	0.7119
To Agent 2	0.3333	-0.2078	0.0000	0.0000
To Agent 3	0.3333	0.2792	0.1753	0.2881

4.5.2 Using Utility Functions to Determine Risk Exchanges

Following the work of De Finetti (1940), intellectual development of risk exchanges was subsequently reignited by contributions due to Karl Borch, summarized in Borch (1974). Borch focused on economic modeling using utility theory. To keep this treatment self-contained, a brief overview of utility theory can be found in Section 4.6.3.

In this context, the $i$th firm or agent has an initial wealth $w_i$, faces potential losses $X_i$, and values money using the utility function $U_i(\cdot)$. Before the risk exchange, its expected utility is $\mathrm{E}[U_i(w_i - X_i)]$. As in equation (4.12), a set of risk exchange rules is denoted by $g_i$, so that after the exchange, one is responsible for the loss $Y_i = g_i(X_1, \ldots, X_n)$. After the risk exchange, the expected utility is $\mathrm{E}[U_i(w_i - Y_i)]$. Recall that a risk exchange is said to be Pareto optimal if it is not possible to improve the situation of one company without worsening the situation of at least one other company.

Theorem (Borch). An exchange $\{g_1, \ldots, g_n\}$ is Pareto-optimal if and only if there exist non-negative constants $k_1, \ldots , k_n$ such that, with probability one, $k_i~ U_i'[w_i - g_i(X_1, \ldots, X_n)]$ is the same for all $i$.

Before discussing the implications of this result, let us first see how it works in a special case.

Example 4.5.2. Exponential Utility Functions. Suppose that each agent has an exponential utility function of the form $U_i(x) = \alpha_i[1-\exp(-x/\alpha_i)]$. In this case, the solution of Borch’s Theorem is a familiar quota share treaty with agent $i$’s responsibility being $Y_i = c_i~ S + P_i$, where \[ c_i = \frac{\alpha_i}{\alpha_1 + \cdots + \alpha_p} \ \ \ \text{and} \ \ \ P_i = w_i - c_i\sum_{j=1}^n \left[w_j + \alpha_j \ln \frac{k_i}{k_j} \right] . \] Thus, each company takes a proportional share $c_i$ of the overall risk pool, $S =X_1 + \cdots + X_n$. To equalize the transactions, cash side-payments in the form of $P_i$ are made.

As summarized by Lemaire (1991):

This kind of exchange is common in reinsurance practice. Each agent will pay a share $c_i$ of each claim, inversely proportional to risk aversion $\alpha_i$.
In order to compensate for the fact that the least risk-averse companies will pay greater claim amounts, zero-sum ($\sum_i P_i = 0$) side-payments or “fees” $P_i$ between the participants occur.
Note that the quota proportions are determined by the risk-aversion parameters only: they are non-negotiable. Hence the bargaining process will involve only the monetary compensations. Stated another way, agents will negotiate about amounts of money, not about abstract bargaining constants $k_i$.
It turns out that quota-share treaties with side-payments also occur when all exchange participants use quadratic or logarithmic utilities, and only in those cases. In these cases, both the quotas and the monetary compensations will be subject to negotiation.

$Under~the~Hood.$ Development of the Exchange for Exponential Utility Functions

Example 4.5.2 helps to underscore some additional features of Borch’s theorem from, for example, Lemaire (1991):

First, note that the condition of the theorem does not depend on the loss amount distributions. There is no mention of the shape of the distribution, the number of moments required, or any other restrictions.

Second, in the exponential utility example, we saw that the exchange rules only depend on the sum of losses, $S=X_1 + \cdots + X_n$ although we allowed for more general functions of the form $g_i(X_1, \ldots, X_n)$. This is true more broadly under mild regularity conditions such as, for example, requiring differentiability of $g_i$.

From Borch (1962), a Pareto-optimal allocation can be achieved by choosing positive constants $k_1, \ldots, k_n$ and trying to maximize $\sum_{i=1}^n k_i~ \mathrm{E}[U_i(X_i)]$. We may interpret the positive constants as weighting factors to equalize contributions of each company.

It is important to remark that the whole model relies on two important implicit assumptions:

Shared beliefs: All companies use the same joint distribution of claim amounts.
Truthfulness: All companies honestly report the utility function that represents their attitude toward risk.

4.5.3 Conditional Mean Risk-Sharing Rule

Another type of risk exchange assumes that all risks go into a central pool. Now denote the pool risk as $S_n = X_1 + \cdots + X_n$, the total amount to be exchanged with conditional mean $g_{i,n} (s) = \mathrm{E}[X_i|S_n = s]$. With the conditional mean risk-sharing rule, the $i$th participant’s share of the total risk is $Y_i = g_{i,n} (S_n)$. Denuit and Robert (2021a) refers to this setting as a self-governing, or no insurance company, model.

Using conditional expectations, it is straightforward to check that this rule satisfies the market clearing and fairness conditions, that is, that $\sum_i X_i = S_n = \sum_i Y_i$ and that $\mathrm{E}(X_i) = \mathrm{E}(Y_i)$. Moreover, from Jensen’s inequality for conditional expectations, we have that \[ \mathrm{E} [U_i(w_i - X_i)] \le \mathrm{E} [U_i(w_i -g_{i,n}(S_{n}))], \ \ \ i=1, \ldots, n, \] for concave utility functions $U_i$ and initial wealth levels $w_i$. Thus, the conditional mean risk allocation benefits all risk‐averse economic agents, thereby improving their risk position. Moreover, under some mild regularity conditions (when $g_{i,n}(s)$ is non-decreasing in $s$ for all $i$), the conditional mean risk-sharing rule is Pareto-optimal.

As an example of other results, Denuit and Robert (2021a) also shows \[ \mathrm{E} [U_i(w_i - g_{i,n}(S_{n}))] \le \mathrm{E} [U_i(w_i - g_{i,n+1}(S_{n+1})], \ \ \ i=1, \ldots, n . \] We may interpret this to mean the risk position of the $i$th participant improves as the exchange pool becomes larger. They also cite asymptotic results about the pool (as it grows larger), such as law of large numbers and central limit theorem type results, that give qualitative information about the behavior of large pools.

Example 4.5.3. Conditional Mean Risk-Sharing Among Three Agents. This is a continuation of Example 4.5.1 with the same means and variances for $n=3$ agents. In Example 4.5.1, we only needed means and variances but now supplement this by assuming that the first and third agents follow a gamma distribution while the second agent follows a Pareto distribution. Further, the correlations of Example 4.5.1 are now treated as association parameters for a Gaussian copula to allow for dependencies.

With knowledge of the entire distribution of the losses $\{X_1, X_2, X_3\}$, one can calculate the conditional mean risk-sharing rules via simulation. With simulated observations, I use nonparametric regression techniques as described in, for example, Härdle (1990) (Chapter 3). Specifically:

For $r=1 , \ldots, R$, generate simulated losses $\{X_1^r, X_2^r, X_3^r\}$ and sum them to get $S^r$.
From simulated outcomes $\{S^r\}$, build a nonparametric density estimator $\hat{f}_{S}(s)$. This appears in the left-hand panel of Figure 4.8.
For different values of $s$, calculate the estimator \[ \hat{g}_j(s) = \frac{\sum_{r=1}^R X_j^r \times I( s - bw \le S^r \le s+bw)}{\sum_{r=1}^R I( s - bw \le S^r \le s+bw)}, \ \ \ j=1,2,3, \] where $bw$ is known as a bandwidth for the estimator (we use $bw=1$ in our example). In this literature, this is sometimes called a Nadaraya-Watson estimator. These appear in the middle panel of Figure 4.8. It is also of interest to examine the proportion of the realized risk ($S=s$) taken on by each agent, $\hat{g}_j(s)/s$. These appear in the right-hand panel.

R Code for Example 4.5.3

num.row = 3
ones.vec <- as.vector(rep(1,num.row))
ones.mat <- matrix (rep(1,num.row^2),nrow = num.row)
X.sigma = matrix(c(10, -4 , -1 , -4 , 8 , 1, -1 ,  1 , 1), nrow = num.row)
X.var <- diag(X.sigma)
stdmat <- sqrt(diag(X.var,nrow=num.row, ncol=num.row))
X.corr <- solve(stdmat) %*% X.sigma%*% solve(stdmat)
corrparams <- X.corr[lower.tri(X.corr)]
mu = as.vector(c( 20, 2.5, 10))

library(copula)
library(actuar)
#  Set Simulation Parameters
nsim       <- 20000
set.seed(202020)
#  Normal, or Gaussian, Copula
norm.cop   <- copula::normalCopula(param=corrparams, dim = 3,'dispstr' ="un") 
UCop       <- copula::rCopula(nsim, norm.cop)
#  Gamma Marginal Distributions
# scale= Var/Mean, shape = Mean/scale
# Pareto Marginal Distribution
# shape = 0.5*var/(var-mean^2), scale= mean*(shape-1)
risk1scale <- X.var[1]/mu[1]
risk1shape <- mu[1] / risk1scale
risk3scale <- X.var[3]/mu[3]
risk3shape <- mu[3] / risk3scale
risk2shape <- 2 * X.var[2] / (X.var[2]- mu[2]^2)
risk2scale <- mu[2]*(risk2shape - 1)

# Random variables
X1 <- qgamma(p=UCop[,1],shape = risk1shape, scale = risk1scale)
X2 <- actuar::qpareto(p=(UCop[,2]),shape = risk2shape, scale = risk2scale)
X3 <- qgamma(p=UCop[,3],shape = risk3shape, scale = risk3scale)
S  <- X1 + X2 + X3

LowQuan  <- quantile(S, p = 0.05)
HighQuan <- quantile(S, p = 0.95)
sVec     <- seq(from=LowQuan, to=HighQuan, length.out=91)
Results  <- matrix(0, nrow = 3, ncol = length(sVec))
bw       <- 1
for (i in 1:length(sVec) ){
  num <- sum((S>=sVec[i]-bw)*(S < sVec[i]+bw))
  Results[1,i] <- sum(X1*(S>=sVec[i]-bw)*(S < sVec[i]+bw)) / num
  Results[2,i] <- sum(X2*(S>=sVec[i]-bw)*(S < sVec[i]+bw)) / num
  Results[3,i] <- sum(X3*(S>=sVec[i]-bw)*(S < sVec[i]+bw)) / num  
  }

densS <- density(S,from =LowQuan, to=HighQuan, n=91)
# Varh1 <- sum(densS$y*Results[1,]^2)/sum(densS$y) - mu[1]^2
# Varh2 <- sum(densS$y*Results[2,]^2)/sum(densS$y) - mu[2]^2
# Varh3 <- sum(densS$y*Results[3,]^2)/sum(densS$y) - mu[3]^2

Meanh1 <- sum(densS$y*Results[1,])/sum(densS$y) 
Meanh2 <- sum(densS$y*Results[2,])/sum(densS$y) 
Meanh3 <- sum(densS$y*Results[3,])/sum(densS$y) 

VarhA1 <- sum(densS$y*(Results[1,]-Meanh1)^2)/sum(densS$y) 
VarhA2 <- sum(densS$y*(Results[2,]-Meanh2)^2)/sum(densS$y) 
VarhA3 <- sum(densS$y*(Results[3,]-Meanh3)^2)/sum(densS$y) 

par(mfrow=c(1,3))
  plot(density(S), main= "", xlim = c(25, 50), 
     xlab="Sum of Risks", yaxt = "n" )
    axis(side=2, las=2) 
  plot(sVec, Results[1,] , ylim = c(0,25), col = FigGreen, 
     ylab = "Share of Risks", xlab = "Sum of Risks", 
     yaxt = "n", type = "l",lty = 3 , lwd = 2.0)
    axis(side=2, las=2) 
    lines(sVec, Results[2,], col = FigRed, lty = 2)
    lines(sVec, Results[3,], col = "black",  lty = 1)
  plot(sVec, Results[1,]/sVec , ylim = c(0,0.7), col = FigGreen, 
     ylab = "Proportion of Risks", xlab = "Sum of Risks", 
     yaxt = "n", type = "l",lty = 3 , lwd = 2.0)
    axis(side=2, las=2) 
    lines(sVec, Results[2,]/sVec, col = FigRed, lty = 2)
    lines(sVec, Results[3,]/sVec, col = "black",  lty = 1)

From Example 4.5.1, recall that the sum of the means was $20+ 2.5+ 10 = 32.5$; this is consistent with the density plot in the left-hand panel of Figure 4.8. The third risk had a mean of 10 and a variance of 1; so when we examine its risk-sharing behavior as the solid black line, the middle panel shows it is relatively level (about the mean of 10) whereas the right-hand panel shows that its proportion decreases as the sum of (realized) risks, $S=s$, increases. In contrast, the second risk is the more volatile Pareto risk, depicted as the red dashed line. This risk’s conditional mean proportion increases as $s$ increases. The first risk, the other gamma distributed random variable, serves as a balancing item for the other two (balancing because the sum of the three risks must add to $s$). The conditional mean for this risk increases as $s$ increases but decreases when viewed as a proportion of the total risk $s$.

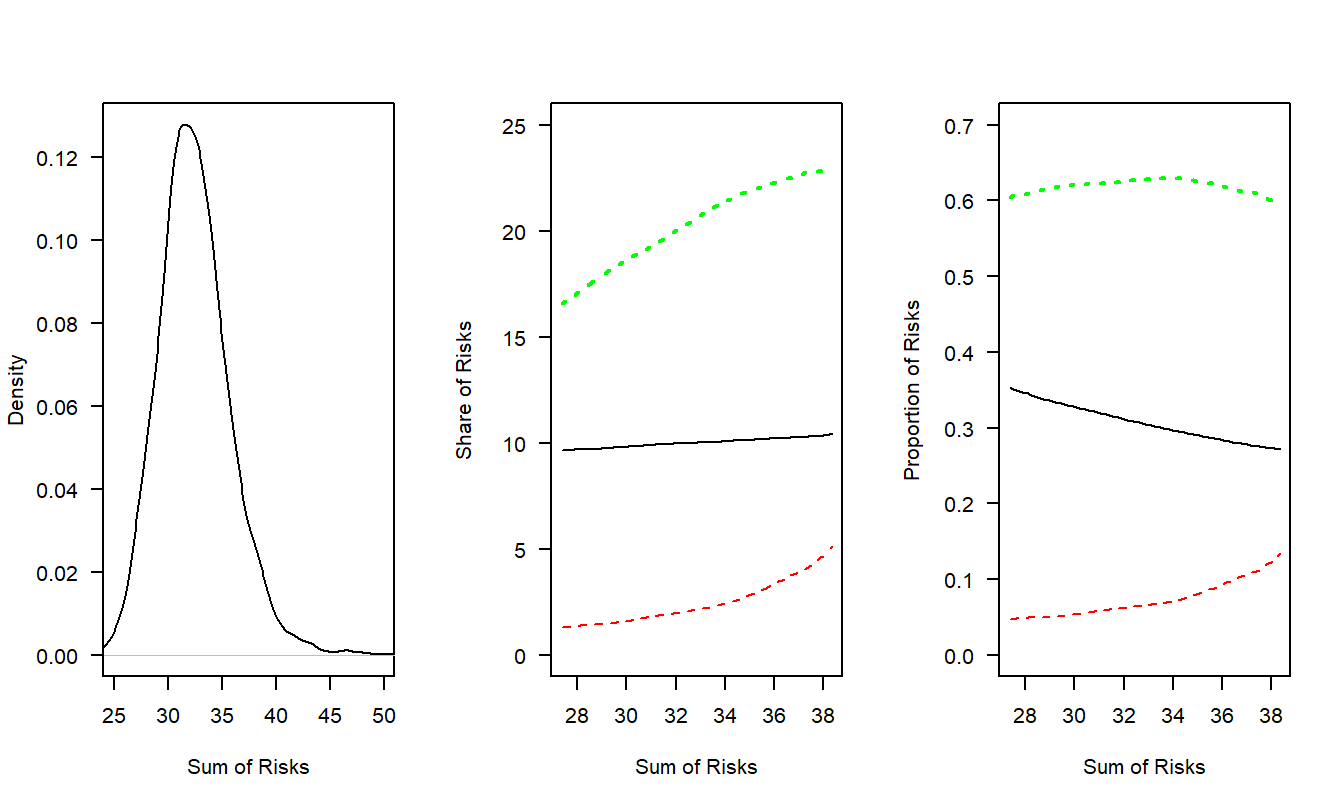
Sharing Risks using the Conditional Mean Risk-Sharing Rule. The green dotted line corresponds to risk 1, the black solid line is for risk 2, and the red dashed line is for risk 3.

Figure 4.8: Sharing Risks using the Conditional Mean Risk-Sharing Rule. The green dotted line corresponds to risk 1, the black solid line is for risk 2, and the red dashed line is for risk 3.

One can also compare the results from the analysis in Example 4.5.1 for the Section 4.5.1 proportional risk-sharing rules to those from the conditional mean sharing rules. Table 4.9 provides this comparison, extending the results reported in Table 4.7 to include those from the conditional mean sharing rules. As in Table 4.7, the first column of Table 4.9 gives the original (prior to the exchange) variances for each agent and columns two through five gives optimal variances imposing more conditions on the proportional risk-sharing rules. The right-hand column shows variances of each agent assuming that a conditional mean sharing rule is in place.

Not surprisingly, these compared favorably to other rules considered. Recall that the Section 4.5.1 rules use only information from the first two moments and restrict consideration to proportional sharing rules. In contrast, the conditional mean sharing rule requires knowledge of the entire joint distribution to compute the conditional means.

Table 4.9: **Risk Exchange Model Variances**
	Original	Clear Exchange	No Profits	Short Sell	Risk Improve	Conditional Mean
Agent 1	10	1.2222	2.6281	2.8881	3.3164	2.6257
Agent 2	8	1.2222	0.6695	0.3415	0.4148	0.5706
Agent 3	1	1.2222	1.1359	1.3959	1.0000	0.0289
Total	19	3.6667	4.4335	4.6256	4.7312	3.2251

Video: Section Summary

4.6 Supplemental Materials

4.6.1 Further Resources and Readings

There are many superb treatments of reinsurance in the literature. An outstanding book-long introduction is Albrecher, Beirlant, and Teugels (2017); see also Verlaak and Beirlant (2003).

Lourdes Centeno and Simões (2009) identify the pioneering work by Bruno de Finetti in 1940, De Finetti (1940), as the first treatment of risk sharing in the academic literature. Especially with the variance as a measure of uncertainty, Beard, Pentikäinen, and Pesonen (1984) summarizes work that influenced generations of actuaries.

The Section 4.4.1 asset allocation problem has already been discussed in Sections 1.3 and 3.4. Additional details on asset allocations can be found in Ingersoll (1987) and Panjer et al. (1998) (Chapter 8).

In addition to the references already cited in Section 4.5.2 on utility based risk exchanges, see H. U. Gerber (1979) and Albrecher, Beirlant, and Teugels (2017) for further discussions and references to this fascinating literature. An accessible proof of Borch’s Theorem in Section 4.5.2 may be found in H. Gerber and Pafumi (1998). The Section 4.5 risk exchanges are motivated by pooling of risks that are generally viewed as beneficial for both insurance firms, the suppliers of insurance, as well consumers, who demand insurance. For example, Albrecht and Huggenberger (2017) provide general conditions under which consumers with exchangeable risks will improve their risk positions by pooling (exchangeable risks have the same distribution but may exhibit some positive dependence, a generalization of the idea of “i.i.d.” - independent and identically distributed risks). However, as demonstrated in Exercise 4.5.1, pooling can fail when risks have different distributions, the so-called heterogeneous case.

The conditional mean risk-sharing rule is due to Denuit and Dhaene (2012). The peer-to-peer risk exchange development in Section 4.5.3 follows the work of Denuit and Robert (2021a). Further exploration of this topic appears in Section 6.5.

4.6.2 Exercises

Section 4.1 Exercise

Exercise 4.1.1. Portfolio Management. Let us consider the same structure as in Exercise 2.2.2, with risks:

$X_1$ - buildings, modeled using a gamma distribution with mean 200 and scale parameter 100.
$X_2$ - motor vehicles, modeled using a gamma distribution with mean 400 and scale parameter 200.
$X_3$ - directors and executive officers risk, modeled using a Pareto distribution with mean 1000 and scale parameter 1000.
$X_4$ - cyber risks, modeled using a Pareto distribution with mean 1000 and scale parameter 2000.

Denote the total risk as $S = X_1 + X_2 + X_3 + X_4$. For simplicity, in this exercise we assume that these risks are independent.

To manage the risk, you seek some reinsurance protection. You wish to manage internally small and intermediate building and motor vehicles amounts, up to $u_1$ and $u_2$, respectively. That is, your retained risk is $Y_{retained}= \min(X_1,u_1) + \min(X_2,u_2)$. You seek reinsurance to cover all other risks. Specifically, the reinsurer’s portion is \[ Y_{reinsurer} = S- Y_{retained}=(X_1 - u_1)_+ + (X_2 - u_2)_+ + X_3 + X_4 . \] Using upper limits $u_1=$ 100 and $u_2=$ 200, this example will:

a. Determine the expected claim amount of (i) that retained, (ii) that accepted by the reinsurer, and (iii) the total overall amount.
b. Determine the 80th, 90th, 95th, and 99th percentiles for (i) that retained, (ii) that accepted by the reinsurer, and (iii) the total overall amount.
c. Compare the distributions by plotting the densities for (i) that retained, (ii) that accepted by the reinsurer, and (iii) the total overall amount.

Show Exercise 4.1.1 Solution with R Code

Section 4.3 Exercise

Exercise 4.3.1. Sensitivity of Optimal Quota Share Proportions. Consider the quota share problem with dependent risks described in Section 4.3.2. How sensitive are these optimal proportions to small changes in $\boldsymbol \Sigma$? One can derive explicit results in the simpler case where we do not impose non-negative constraints on the parameters. The more general problem, with non-negativity constraints, will be taken up in Chapter 10.

Specifically, if we let $\sigma$ be a generic element of $\boldsymbol \Sigma$, show that \[\begin{equation} \begin{array}{ll} \partial_{\sigma} \mathbf{c} &=\left(\partial_{\sigma} LME \right) \frac{1}{2} ~\boldsymbol \Sigma^{-1} ~\mathrm{E} (\mathbf{X}) - \frac{LME}{2} ~ \boldsymbol\Sigma^{-1} \left(\partial_{\sigma}\boldsymbol \Sigma\right) \boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X}) ,\\ \end{array} \tag{4.14} \end{equation}\] where \[\begin{equation} \begin{array}{rl} & \partial_{\sigma} LME = LME~\frac{\mathrm{E}(\mathbf{X})^{\prime} ~\boldsymbol \Sigma^{-1} \left(\partial_{\sigma}\boldsymbol \Sigma\right) \boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X}) }{~\mathrm{E}(\mathbf{X})^{\prime} ~\boldsymbol \Sigma^{-1} ~\mathrm{E}(\mathbf{X})} .\\ \end{array} \tag{4.15} \end{equation}\]

Solution to Exercise 4.3.1

Section 4.4 Exercise

Exercise 4.4.1. Markowitz Investment Optimal Allocations. Recall the notation from Section 3.4 on the asset allocation problem. In this exercise, we do not require $c_i \ge 0$, so that “short sales” are permitted, yet do require $\sum_i c_i =1$. With this assumption, show that the optimal allocations can be expressed as \[\begin{equation} \mathbf{c} = \mathbf{c}(LME_1, LME_2) = LME_1 ~\boldsymbol \Sigma^{-1} [\mathrm{E}(\mathbf{R})] +LME_2 ~\boldsymbol \Sigma^{-1} \mathbf{1} , \tag{4.16} \end{equation}\] where \[\begin{equation} {\small LME_1 = \frac{A_1A_3-A_2^2}{Req_0 ~A_3-A_2} ~~~~~~~ LME_2 = \frac{A_2^2 - A_1A_3}{Req_0 ~A_2-A_1} } \tag{4.17} \end{equation}\]

and $A_1=\mathrm{E}(\mathbf{R})^{\prime}\boldsymbol \Sigma^{-1} \mathrm{E}(\mathbf{R})$, $A_2=\mathbf{1}^{\prime}\boldsymbol \Sigma^{-1} \mathrm{E}(\mathbf{R})$, and $A_3=\mathbf{1}^{\prime}\boldsymbol \Sigma^{-1} \mathbf{1}$.

Solution to Exercise 4.4.1

Section 4.5 Exercises

Exercise 4.5.1. Risk Sharing Does not Always work with Heterogeneous Risks. Consider a set of independent risks $X_j$ that have the same mean (say $\mu$) with variances $\sigma_j^2$ that are possibly different.

a. Suppose that two risks are shared equally so that $Y_1 = (X_1 + X_2)/2 = Y_2$ but that the first risk has a higher variance such that $\sigma_1^2 = 4$ and $\sigma_2^2 = 1$. Show that this risk sharing arrangement improves the risk position for the first risk but not the second. That is, show that \[ \mathrm{Var}(Y_1) \le \mathrm{Var}(X_1) \ \ \ \ \text{and} \ \ \ \mathrm{Var}(Y_2) \ge \mathrm{Var}(X_2) . \] b. Suppose that $n$ risks are shared equally so that $Y_j = (X_1 + \cdots +X_n)/n$ but that the first risk has a higher variance $\sigma_1^2$ and other risks have equal variance, say $\sigma_2^2$. Show that the risk position for all other risks improves only if $\sigma_1^2$ is not too large relative to the others. Specifically, show that $\mathrm{Var}(Y_j) \le \mathrm{Var}(X_j)$ if $\sigma_1^2 \le (n^2-n+1) \sigma_2^2$.
c. For two risks, suppose that the first risk takes $Y_1 =c X_1 + (1-c) X_2$ and the second takes $Y_2 = (X_1+X_2) - Y_1$ $= (1-c) X_1 + c X_2$. Show that the variability of each risk must be relatively similar for risk improvement for both risks. Specifically, for $\mathrm{Var}(Y_j) \le \mathrm{Var}(X_j)$, $j=1,2$, we require $\sigma_2^2 k_c \le \sigma_1^2 \le \sigma_2^2/k_c$, with the constant $k_c = (1-c)/(1+c)$.

Solution to Exercise 4.5.1

Exercise 4.5.2. Optimal Linear Exchange Based on a Clearing Exchange Condition. Based on the risk sharing structure described in Section 4.5.1, now use only the exchange clearing condition for this problem. The goal is to determine the set of risk sharing/allocation parameters $c_{ij}$ that \[ \boxed{ \begin{array}{lc} {\small \text{minimize}}_{\bf C} & \sum_i \mathrm{Var} (Y_i) \\ {\small \text{subject to}} & \mathbf{C}' {\bf 1}= {\bf 1} . \end{array} } \]

a. Show that the solution is given as \[\begin{equation} \begin{array}{ll} \mathbf{C}_{opt} &= \frac{1}{n}{\bf 1} {\bf 1}' .\\ \end{array} \tag{4.18} \end{equation}\]

b. Show that the variance is \[ \begin{array}{ll} \mathbf{C}_{opt} \boldsymbol \Sigma \mathbf{C}_{opt}' &= \frac{k_{\Sigma}}{n^2}{\bf 1} {\bf 1}' .\\ \end{array} \]

with the constant $k_{\Sigma}= {\bf 1}'\boldsymbol \Sigma {\bf 1}$.

Solution to Exercise 4.5.2

Exercise 4.5.3. Optimal Linear Exchange with Clearing Exchange and No Profits Conditions. Continuing from Exercise 4.5.2, now add to the exchange clearing the no profits condition. As before, the goal is to find a set of risk sharing/allocation parameters $c_{ij}$ that minimize, for example, the system variance $\sum_{i=1}^n \mathrm{Var} (Y_i)$. In summary, \[ \boxed{ \begin{array}{lc} {\small \text{minimize}}_{\bf C} & \sum_i \mathrm{Var} (Y_i) \\ {\small \text{subject to}} & \mathbf{C} \boldsymbol \mu = \boldsymbol \mu \ \ \ \text{ and } \mathbf{C}' {\bf 1}= {\bf 1} . \end{array} } \] a. Show that the solution is given as \[\begin{equation} \begin{array}{ll} \mathbf{C}_{opt} &= \frac{1}{n} {\bf 1}{\bf 1}' + \frac{1}{k_{\mu}} \boldsymbol \mu^*~\boldsymbol \mu'\boldsymbol \Sigma ^{-1} . \end{array} \tag{4.19} \end{equation}\] with the constant $k_{\mu}= \boldsymbol \mu'\boldsymbol \Sigma^{-1} \boldsymbol \mu$ and the deviations from the means vector $\boldsymbol \mu^* = \boldsymbol \mu- {\bar{\mu}} {\bf 1}$. Note that this vector is zero when the means are constant.

b. Show that the variance is \[\begin{equation} \begin{array}{ll} \mathbf{C}_{opt} \boldsymbol \Sigma \mathbf{C}_{opt}' &=\frac{1}{n^2} k_{\bf 1} {\bf 1}{\bf 1}' + \frac{1}{k_{\mu}} \bar{\mu} \left[ \boldsymbol \mu^* {\bf 1}' + {\bf 1} {\boldsymbol \mu^*}' \right] + \frac{1}{k_{\mu}} {\boldsymbol \mu^*} {\boldsymbol \mu^*}' . \\ \end{array} \tag{4.20} \end{equation}\] where we recall the constant $k_{\Sigma}= {\bf 1}'\boldsymbol \Sigma {\bf 1}$.

Solution to Exercise 4.5.3

Check: For the minimization, we again use the method of Lagrange multipliers. The Lagrangian is

\[ LA(\mathbf{C}) =trace(\mathbf{C} \boldsymbol \Sigma \mathbf{C}') + {\boldsymbol \lambda}_1' (\mathbf{C} \boldsymbol \mu -\boldsymbol \mu ) + {\boldsymbol \lambda}_2' (\mathbf{C}' {\bf 1} -{\bf 1} ) . \]

Taking derivatives, we get

\[ \begin{array}{ll} {\bf 0}=\frac{\partial ~LA(\mathbf{C})}{\partial ~\mathbf{C}} &= \frac{\partial }{\partial ~\mathbf{C}} trace(\mathbf{C} \boldsymbol \Sigma \mathbf{C}') + \frac{\partial }{\partial ~\mathbf{C}}{\boldsymbol \lambda}_1' \mathbf{C} \boldsymbol \mu + \frac{\partial }{\partial ~\mathbf{C}} {\bf 1}' \mathbf{C} {\boldsymbol \lambda}_2 \\ &= 2\mathbf{C} \boldsymbol \Sigma +{\boldsymbol \lambda}_1 \boldsymbol \mu' + {\bf 1}{\boldsymbol \lambda}_2 '. \\ \end{array} \tag{4.21} \]

Thus,

\[ \begin{array}{ll} \mathbf{C}_{opt} &= -\frac{1}{2} {\boldsymbol \lambda}_{1,opt} \boldsymbol \mu'\boldsymbol \Sigma ^{-1} - \frac{1}{2} {\bf 1}{\boldsymbol \lambda}_{2,opt}'\boldsymbol \Sigma ^{-1} \\ \end{array} \tag{4.22} \]

Now, pre-multiply the expression in equation (4.21) by ${\bf 1}'$ to get

\[ \begin{array}{ll} {\bf 0} &= 2{\bf 1}'\mathbf{C} \boldsymbol \Sigma +{\bf 1}'{\boldsymbol \lambda}_1 \boldsymbol \mu' + {\bf 1}'{\bf 1}{\boldsymbol \lambda}_2 '. \\ &= 2{\bf 1}' \boldsymbol \Sigma +{\bf 1}'{\boldsymbol \lambda}_1 \boldsymbol \mu' + n{\boldsymbol \lambda}_2 '. \\ \rightarrow & {\boldsymbol \lambda}_2= -\frac{1}{n} \left(\boldsymbol \mu {\boldsymbol \lambda}_1 '{\bf 1} + 2 \boldsymbol \Sigma {\bf 1} \right) \end{array} \tag{4.23} \]

Post-multiply the expression in equation (4.21) by $\boldsymbol \Sigma^{-1} \boldsymbol \mu$ to get

\[ \begin{array}{ll} 0&= (2\mathbf{C} \boldsymbol \Sigma +{\boldsymbol \lambda}_1 \boldsymbol \mu' + {\bf 1}{\boldsymbol \lambda}_2 ')\boldsymbol \Sigma^{-1} \boldsymbol \mu \\ &= 2 \mathbf{C} \boldsymbol \mu + k_{\mu} {\boldsymbol \lambda}_1 -\frac{1}{n} {\bf 1}( 2{\bf 1}' \boldsymbol \Sigma +{\bf 1}'{\boldsymbol \lambda}_1 \boldsymbol \mu') \boldsymbol \Sigma^{-1} \boldsymbol \mu\\ &= 2 \boldsymbol \mu + k_{\mu} {\boldsymbol \lambda}_1 -\frac{1}{n} 2{\bf 1}{\bf 1}' \boldsymbol \mu - \frac{1}{n}{\bf 1}{\bf 1}'{\boldsymbol \lambda}_1 k_{\mu}\\ &= 2 (\boldsymbol \mu - {\bf 1}\bar{\mu}) + k_{\mu} ({\boldsymbol \lambda}_1 - {\bf 1} \frac{1}{n}{\bf 1}'{\boldsymbol \lambda}_1 )\\ \rightarrow & {\boldsymbol \lambda}_1 = -\frac{2}{k_{\mu}} \boldsymbol \mu .\\ \end{array} \]

Inserting this into equation (4.23) yields

\[ \begin{array}{ll} {\boldsymbol \lambda}_2 &= -\frac{1}{n} \left(\boldsymbol \mu {\boldsymbol \lambda}_1 '{\bf 1} + 2 \boldsymbol \Sigma {\bf 1} \right) \\ &= \frac{2}{n k_{\mu}} \left(\boldsymbol \mu \boldsymbol \mu'{\bf 1} - k_{\mu}\boldsymbol \Sigma {\bf 1} \right) .\\ \end{array} \]

Summarizing, we have

\[ \begin{array}{ll} \mathbf{C}_{opt} &= -\frac{1}{2} {\boldsymbol \lambda}_{1,opt} \boldsymbol \mu'\boldsymbol \Sigma ^{-1} - \frac{1}{2} {\bf 1}{\boldsymbol \lambda}_{2,opt}'\boldsymbol \Sigma ^{-1} \\ {\boldsymbol \lambda}_{1,opt} &= -\frac{2}{k_{\mu}} \boldsymbol \mu \\ {\boldsymbol \lambda}_{2,opt} &= \frac{2}{n k_{\mu}} \left(\boldsymbol \mu \boldsymbol \mu'- k_{\mu}\boldsymbol \Sigma \right) {\bf 1} \\ \end{array} \]

With this, we have

\[ \begin{array}{ll} \mathbf{C}_{opt} &= -\frac{1}{2} {\boldsymbol \lambda}_{1,opt} \boldsymbol \mu'\boldsymbol \Sigma ^{-1} - \frac{1}{2} {\bf 1}{\boldsymbol \lambda}_{2,opt}'\boldsymbol \Sigma ^{-1} \\ &= \frac{1}{k_{\mu}}\boldsymbol \mu \boldsymbol \mu'\boldsymbol \Sigma ^{-1} - \frac{1}{nk_{\mu}}{\bf 1}{\bf 1}'\left[ \boldsymbol \mu \boldsymbol \mu' - k_{\mu}\boldsymbol \Sigma \right] \boldsymbol \Sigma ^{-1} \\ &= \frac{1}{k_{\mu}} \boldsymbol \mu \boldsymbol \mu'\boldsymbol \Sigma ^{-1} - \frac{1}{k_{\mu}} \frac{{\bf 1}'\boldsymbol \mu}{n}{\bf 1} \boldsymbol \mu'\boldsymbol \Sigma ^{-1} + \frac{1}{n} {\bf 1}{\bf 1}' \\ &= \frac{1}{k_{\mu}} (\boldsymbol \mu - \bar{\mu} {\bf 1})\boldsymbol \mu'\boldsymbol \Sigma ^{-1} + \frac{1}{n} {\bf 1}{\bf 1}' . \\ \end{array} \]

With $\boldsymbol \mu^* = \boldsymbol \mu- {\bar{\mu}} {\bf 1}$, this is sufficient for equation (4.19).

As a check, we can see that the solution satisfies the constraints, and so

\[ \begin{array}{ll} \mathbf{C}_{opt} \boldsymbol \mu &= \frac{1}{k_{\mu}} (\boldsymbol \mu - \bar{\mu} {\bf 1})\boldsymbol \mu'\boldsymbol \Sigma ^{-1} \boldsymbol \mu + \frac{1}{n} {\bf 1}{\bf 1}' \boldsymbol \mu \\ &= \frac{1}{k_{\mu}} (\boldsymbol \mu - \bar{\mu} {\bf 1}) k_{\mu} + \bar{\mu} {\bf 1} = \boldsymbol \mu. \\ \end{array} \]

For the other constraint, we have

\[ \begin{array}{ll} {\bf 1}'\mathbf{C}_{opt} &= \frac{1}{k_{\mu}} {\bf 1}'(\boldsymbol \mu - \bar{\mu} {\bf 1})\boldsymbol \mu'\boldsymbol \Sigma ^{-1} + \frac{1}{n} {\bf 1}'{\bf 1}{\bf 1}' \\ &= {\bf 0} + \frac{1}{n} n{\bf 1}' = {\bf 1}'. \\ \end{array} \]

Now, define $\mathrm{Var}({ \bf Y}_{opt})= \mathbf{C}_{opt} \Sigma \mathbf{C}_{opt}'$. With this, we have

\[ \begin{array}{ll} \mathbf{C}_{opt} \boldsymbol \Sigma \mathbf{C}_{opt}' &=\left[\frac{1}{n}{\bf 1}{\bf 1}' + \frac{1}{k_{\mu}} \boldsymbol \mu^* \boldsymbol \mu' ~ \boldsymbol \Sigma^{-1} \right]\boldsymbol \Sigma \mathbf{C}_{opt}' \\ &=\left[\frac{1}{n}{\bf 1}{\bf 1}' \boldsymbol \Sigma + \frac{1}{k_{\mu}} \boldsymbol \mu^* \boldsymbol \mu' ~ \right] \left[\frac{1}{n}{\bf 1}{\bf 1}' + \frac{1}{k_{\mu}} ~ \boldsymbol \Sigma^{-1} \boldsymbol \mu {\boldsymbol \mu^*}' \right] \\ &=\frac{1}{n^2} k_{\Sigma} {\bf 1}{\bf 1}' + \frac{1}{k_{\mu}} \bar{\mu} \left[ \boldsymbol \mu^* {\bf 1}' + {\bf 1} {\boldsymbol \mu^*}' \right] + \frac{1}{k_{\mu}} {\boldsymbol \mu^*} {\boldsymbol \mu^*}' \\ \end{array} \]

This is sufficient for the result.

Exercise 4.5.4. Optimal Linear Exchange - Special Case. Based on the risk sharing structure described in Section 4.5.1, now consider a risk exchange where all participants share a proportion of the total risk $\sum_{j=1}^n X_j = {\bf 1' X}$. That is, the allocation matrix is expressed as ${\bf C} = {\bf c 1}'$ and $\bf c$ is an $n \times 1$ vector of coefficients. Check that:

a. The implication of clearing the exchange condition is that ${\bf c' 1} = 1$, that is, the coefficients sum to one.
b. The implication of the no profits condition is that ${\bf c} = \frac{1}{n \bar{\mu}} \boldsymbol \mu$, that is, the coefficient vector equals the mean vector, rescaled by the sum of means. Here, the average mean is denoted as $\bar{\mu} = \frac{1}{n} \bf 1'\boldsymbol \mu$.
c. The implication of the risk improvement condition is that $k_{\Sigma} ~c_i^2 \le \sigma_i^2$ with the constant $k_{\Sigma}= {\bf 1}'\boldsymbol \Sigma {\bf 1}$.
d. Use the parameter values from the Section 4.5.1 example to determine optimal risk exchange variances and coefficients under the

clear exchange,
clear exchange and no short sell, as well as the
clear exchange, no short sell, and risk improvement conditions.

Solutions are provided in Tables 4.10 and 4.11, respectively.

Table 4.10: **Ex 4.5 Risk Sharing Variances**
	Original	Clear Exchange	Short Sell	Risk Improvement
Agent 1	10	1.2222	1.2222	1.3417
Agent 2	8	1.2222	1.2222	1.3417
Agent 3	1	1.2222	1.2222	1.0000
Total	19	3.6667	3.6667	3.6834

Table 4.11: **Ex 4.5 Risk Sharing Coefficients**
	Clear Exchange	Short Sell	Risk Improvement
Agent 1	0.3333	0.3333	0.3492
Agent 2	0.3333	0.3333	0.3492
Agent 3	0.3333	0.3333	0.3015

Solution to Exercise 4.5.4

R Code For Exercise 4.5.4

library(CVXR)
num.row  <- 3
ones.vec <- as.vector(rep(1,num.row))
ones.mat <- matrix (rep(1,num.row^2),nrow = num.row)
X.sigma  <- matrix(c(10, -4 , -1 , -4 , 8 , 1, 
                     -1 ,  1 , 1), nrow = num.row)
X.sigma.inv <- solve(X.sigma)
k.sigma     <- sum(X.sigma)
mu          <- as.vector(c( 20, 3, 10))
#mu = as.vector(c( 4, 6, 1))
Results.mat <- matrix(0,4,4)
Results.mat[1:3,1] <- diag(X.sigma)
Results.mat[4,1]   <- sum(Results.mat[1:3,1])

## Exchange Clearing 
C.vec       <- Variable(3)
#objective  <- quad_form(C.vec, X.sigma) 
objective   <- k.sigma*(C.vec[1]**2 + 
                      C.vec[2]**2 +C.vec[3]**2 )
constraints <- list(sum(C.vec) == 1)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)

C.opt.1     <- result$getValue(C.vec)
Summarize.Result <-function(Condnum,C.opt){
  Y.sigma <- (C.opt %*% ones.vec) %*% 
              X.sigma %*% t(C.opt %*% ones.vec)
  Results.mat[1:3,Condnum+1] <- diag(Y.sigma)
  Results.mat[4,Condnum+1]   <- sum(Results.mat[1:3,Condnum+1])
  return(Results.mat)
  }
Results.mat <- Summarize.Result(Condnum=1,C.opt=C.opt.1)


## Add Limits
C.vec       <- Variable(3)
#objective  <- quad_form(C.vec, X.sigma)  
objective   <- k.sigma*(C.vec[1]**2 + 
                        C.vec[2]**2 +C.vec[3]**2 )
constraints <- list(sum(C.vec) == 1,  C.vec >= 0, C.vec <= 1)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)
C.opt.3     <- result$getValue(C.vec)
Results.mat <- Summarize.Result(Condnum=2,C.opt=C.opt.3)

## Add  Risk Improvement

C.vec       <- Variable(3)
#objective  <- quad_form(C.vec, X.sigma)
objective   <- k.sigma*(C.vec[1]**2 + C.vec[2]**2 +C.vec[3]**2 )
constraints <- list(sum(C.vec) == 1,  C.vec >= 0, C.vec <= 1,
                   k.sigma*C.vec[1]**2 <= X.sigma[1,1],
                   k.sigma*C.vec[2]**2 <= X.sigma[2,2],
                   k.sigma*C.vec[3]**2 <= X.sigma[3,3])
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)
C.opt.4     <- result$getValue(C.vec)
Results.mat <- Summarize.Result(Condnum=3,C.opt=C.opt.4)

# Check short selling
C.opt.mat <- cbind(C.opt.1,C.opt.3,C.opt.4)

rownames(Results.mat) <- c("Agent 1", "Agent 2", 
                           "Agent 3","Total")
colnames(Results.mat) <- c("Original",  "Clear Exchange", 
                           "Short Sell", "Risk Improvement")

TableGen1(TableData=Results.mat, 
         TextTitle='Ex 4.5 Risk Sharing  Variances', 
         Align='rrrrr', Digits=4, ColumnSpec=1:4,
         BorderRight=1 )

Exercise 4.5.5. Following up on Example 4.5.3, modify the code to allow for a larger number of risks so that we can demonstrate the quick computational ability of the convex solvers. As the purpose is to demonstrate the utility of numerical convex solvers, use a random number generator to generate generic mean and variance-covariance matrix (although make sure the variance-covariance matrix remains positive definite). Figure 4.9 demonstrates risk sharing variances under different conditions.

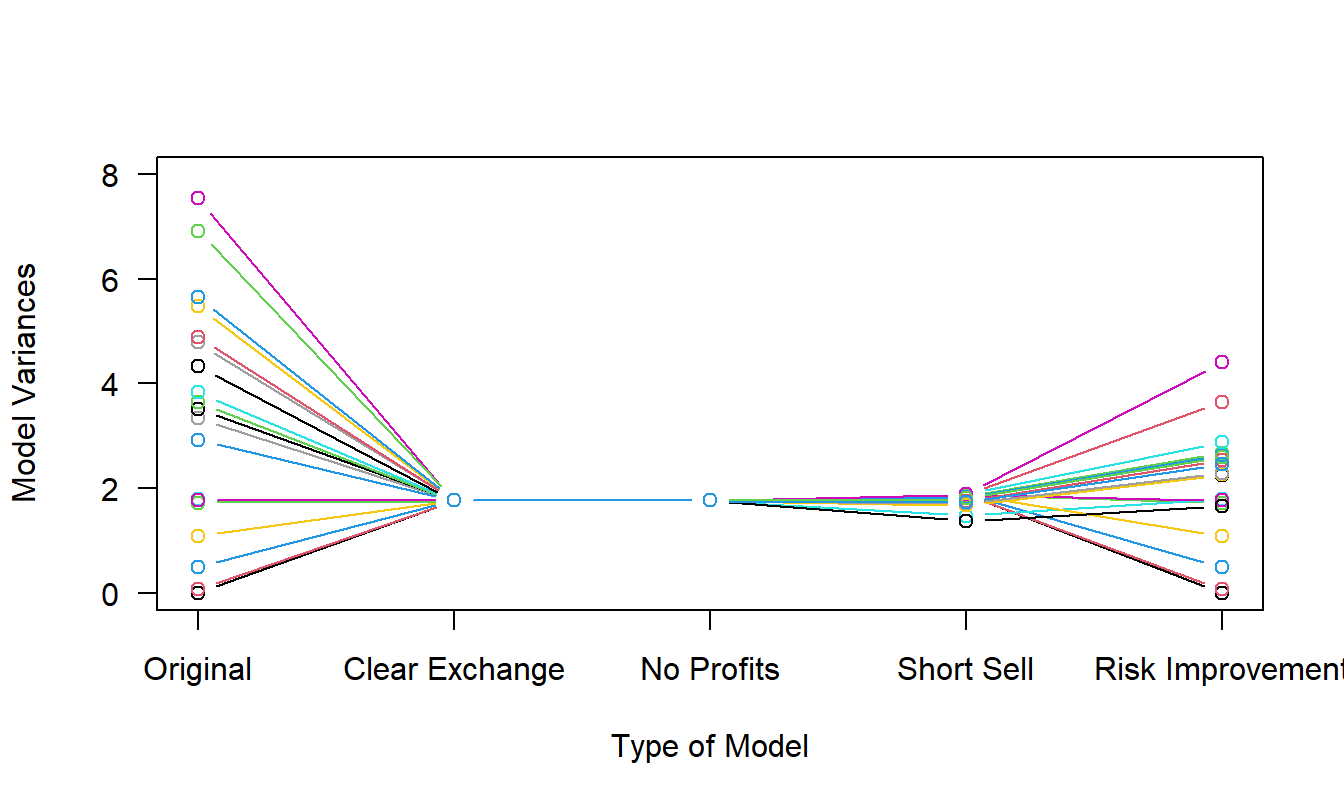
Figure 4.9: Risk Sharing Variances under Different Conditions

Solution to Exercise 4.5.5

library(CVXR)
timestamp <- Sys.time()
num.row   <- 20
set.seed(202122)
ones.vec  <- as.vector(rep(1,num.row))
ones.mat  <- matrix (rep(1,num.row^2),nrow = num.row)
X.Low     <- matrix(runif(num.row*num.row), nrow = num.row, ncol =num.row)
X.Low[upper.tri(X.Low, diag = FALSE)] <- 0
#round(X.Low,digits=3)
X.sigma   <- X.Low %*% t(X.Low)
#round(X.sigma,digits=3)

mu        <- as.vector(runif(num.row))

Results.mat              <- matrix(0,num.row+1,5)
Results.mat[1:num.row,1] <- diag(X.sigma)
Results.mat[num.row+1,1] <- sum(Results.mat[1:num.row,1])

## Exchange Clearing 
C.mat     <- Variable(num.row,num.row)
objective <- quad_form(t(C.mat[1,]), X.sigma)
for (j in 2:num.row){
  objective <- objective + quad_form(t(C.mat[j,]), X.sigma)
  }
constraints <- list(t(C.mat) %*% ones.vec == ones.vec)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)

C.opt.1     <- result$getValue(C.mat)
Summarize.Result <-function(Condnum,C.opt){
  Y.sigma <- C.opt %*% X.sigma %*% t(C.opt)
  Results.mat[1:num.row,Condnum+1] <- diag(Y.sigma)
  Results.mat[num.row+1,Condnum+1] <- 
    sum(Results.mat[1:num.row,Condnum+1])
  return(Results.mat)
  }
Results.mat <- Summarize.Result(Condnum=1,C.opt=C.opt.1)

##  Exchange Clearing  and the No Profits Conditions
constraints <- list(t(C.mat) %*% 
                      ones.vec == ones.vec, C.mat %*% mu == mu)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)
C.opt.2     <- result$getValue(C.mat)
Results.mat <- Summarize.Result(Condnum=2,C.opt=C.opt.2)

## Add Limits
constraints <- list(t(C.mat) %*% ones.vec == ones.vec, 
                    C.mat %*% mu == mu, C.mat >= 0, C.mat <= 1)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)
C.opt.3     <- result$getValue(C.mat)
Results.mat <- Summarize.Result(Condnum=3,C.opt=C.opt.3)

## Add  Risk Improvement
cons        <-  X.sigma[1,1] - quad_form(t(C.mat[1,]), X.sigma)
  for (j in 2:num.row){
  cons <- min_elemwise(cons,X.sigma[j,j] - 
                         quad_form(t(C.mat[j,]), X.sigma) )
  }
constraints <- list(t(C.mat) %*% ones.vec == ones.vec, 
                    C.mat %*% mu == mu, C.mat >= 0, C.mat <= 1,
                    cons >= 0)
prob        <- Problem(Minimize(objective), constraints)
result      <- solve(prob)
C.opt.4     <- result$getValue(C.mat)
Results.mat <- Summarize.Result(Condnum=4,C.opt=C.opt.4)

# Check equality constraints
# t(C.opt.4) %*% ones.vec
# C.opt.4 %*% mu - mu
# Check short selling
#C.opt.3.mat <- cbind(C.opt.1[,3],C.opt.2[,3],
#                     C.opt.3[,3],C.opt.4[,3])

colnames(Results.mat) <- c("Original",  "Clear Exchange", 
                           "No Profits","Short Sell", 
                           "Risk Improvement") -> xlab1
#kableExtra::kable_styling(knitr::kable(Results.mat, digits=4, 
#                   caption="Risk Sharing Model Variances", align = "rrrrr"))

plot(1:5, Results.mat[1,], type = "b", ylim = c(0,8), 
               xlab="Type of Model", ylab=
              "Model Variances", xaxt = "n", yaxt = "n")
axis(side=1, at=1:5, labels=xlab1) 
axis(side=2, las=2) 
if (HtmlEval) {
for (j in 2:num.row){lines(1:5, Results.mat[j,], type = "b", col=j) } 
  } else {
for (j in 2:num.row){lines(1:5, Results.mat[j,], type = "b") }
   }

#Sys.time() - timestamp # n=10 Time difference of 13.05655 secs
# n=20 Time difference of 22.74492 secs (ylim = c(0,8))
# n= 50 Time difference of 3.576095 mins (ylim = c(0,20))

TableGen1(TableData=Results.mat,
         TextTitle='Risk Sharing Model Variances',
         Align='rrrrr', Digits=4, ColumnSpec=1:4,
         BorderRight=1)

Table 4.12: **Risk Sharing Model Variances**
Original	Clear Exchange	No Profits	Short Sell	Risk Improvement
0.0015	1.7649	1.7649	1.8839	0.0015
0.0689	1.7649	1.7649	1.8841	0.0684
1.7236	1.7649	1.7649	1.8698	1.7236
0.4888	1.7649	1.7649	1.8840	0.4888
1.7894	1.7649	1.7649	1.4755	1.7894
1.7689	1.7649	1.7649	1.8832	1.7689
1.0933	1.7649	1.7649	1.8833	1.0933
3.3444	1.7649	1.7649	1.8215	2.6223
3.5171	1.7649	1.7649	1.6750	2.2589
3.6468	1.7649	1.7649	1.8839	3.6468
3.6501	1.7649	1.7649	1.8528	2.6689
2.9202	1.7649	1.7649	1.8327	2.6319
3.8322	1.7649	1.7649	1.8830	2.8750
7.5366	1.7649	1.7649	1.8840	4.4012
5.4658	1.7649	1.7649	1.6768	2.2607
4.7790	1.7649	1.7649	1.7094	2.2976
4.3249	1.7649	1.7649	1.3771	1.6564
4.8820	1.7649	1.7649	1.7564	2.5357
6.9157	1.7649	1.7649	1.8031	2.5940
5.6532	1.7649	1.7649	1.7419	2.4614
67.4026	35.2971	35.2971	35.6615	41.8447

Exercise 4.5.6. Conditional Mean Risk-Sharing Rules. From the notation introduced in Section 4.5.3, we have $w_{i,n} = g_{i,n}(w_n)$ and $B_{i,n} = (w_{i,n} - g_{i,n}(S_n))_+$. Assume that $g_{i,n}(s) = E(X_i |S_n=s)$ is non-decreasing in $s$. Establish that $(w_n - S_n)_+ = \sum_i ~B_{i,n}$.

Solution to Exercise 4.5.6

Exercise 4.5.7. Comparing Proportional to Conditional Mean Risk-Sharing Rules. Following up on Example 4.5.1 and Example 4.5.3, use the statistical code to compare the proportional sharing rules to the conditional mean sharing rules. Compare these two rules by varying the level of dependence. Also examine the effects of changing the marginal distributions to more short-tail (e.g. exponential) and long-tail (e.g., Pareto). What other assumptions do you think might be important? (e.g., how about the number of risks?)

4.6.3 Appendix. Utility Theory

This is a brief review of utility functions, drawn primarily from H. Gerber and Pafumi (1998).

To explain certain phenomena, the usefulness of money can be measured on a new scale. Thus, the usefulness of $x is $U(x)$, the utility (or moral value) of $x. Typically, $x$ is the wealth or a gain of a decision-maker.

Suppose that a utility function $U(x)$ has the following two basic properties:

$U(x)$ is an increasing function of $x$
$U(x)$ is a concave function of $x$.

Usually one assumes that the function $U(x)$ is twice differentiable; then (1) and (2) state that $U'(x) > 0$ and $U''(x) < 0$.

For a given utility function $U(x)$, one can define \[ r(x) = -\frac{U''(x)}{U'(x)} = -\frac{d}{dx} \ln U'(x), \] known as a risk aversion function. Note that properties (1) and (2) imply that $r(x) > 0$. One can check that \[ U(x) = \int^x_{\xi} \exp \left(-\int^z_{\xi} r(y)dy \right)dz \] for some $\xi$, so knowing $U(\cdot)$ and $r(\cdot)$ are equivalent.

Two Applications of Utility Functions

Preference Ordering of Random Gains. Consider a decision-maker with initial wealth $w$ who has the choice between a certain number of random gains. By using a utility function, two random gains can be directly compared: he or she prefers $G_1$ to $G_2$, if \[ \mathrm{E}[U(w + G_1)] > \mathrm{E}[U(w + G_2)]. \] Premium Calculation. We consider a company with initial wealth $w$. The company is to insure a risk and has to pay the total claims $S$ (a random variable) at the end of the period. The expected utility of wealth with the contract should be equal to the utility without the contract: \[ \mathrm{E}[U(w + P - S)] = U(w). \] This is known as the principle of equivalent utility.

Optimality of a Stop-Loss Contract

We consider a company that has to pay the total amount $S$ (a random variable) to its policyholders at the end of the year. We compare two reinsurance agreements:

A stop-loss contract with deductible $d$. Here the reinsurer will pay \[ (S-d)_+ = \left\{ \begin{array}{cl} 0 & \text{if } S<d \\ S-d & \text{if } S > d . \end{array} \right. \]
A general reinsurance contract, given by a function $h(\cdot)$, where the reinsurer pays $h(S)$ at the end of the year. The only restriction on the function $h(\cdot)$ is that $0 \le h(x) \le x$.

We assume that the two contracts are comparable, in the sense that the expected payments of the reinsurer are the same, that is, that $\mathrm{E}[(S - d)_+ ] = \mathrm{E}[h(S)].$ Furthermore, we make the convenient assumption that the two reinsurance premiums are the same. Then, in terms of utility, the stop-loss contract is preferable: \[ \mathrm{E}[U(w - S + h(S))] \le \mathrm{E}[U(w - S + (S - d)_+ )]. \] In this context, $w$ represents the wealth after receipt of the premiums and payment of the reinsurance premiums. For a proof of this result, see H. Gerber and Pafumi (1998) or Proposition 3.2 in Section 3.1.

4.6.4 Appendix. Using Quantile-Based Risk Measures to Determine Risk Exchanges

Another approach to sharing risks, taken to be the redistribution of a total risk among multiple participants, utilizes quantile-based risk measures. To describe the problem, we use the approach of Embrechts, Liu, and Wang (2018) who focus on the range value at risk $RVaR$.

Specifically, consider $n$ agents with the $i$th agent using $RVaR_{\alpha_i, \beta_i}$ to value risks. For notational convenience, suppose that we have aligned the agents so that the last one has the largest $\beta$ parameter, that is, $\beta_n = \max\{\beta_1, \ldots, \beta_n\}$. Further, assume that $\sum_{i=1}^n \alpha_i + \beta_n <1$ and denote the total portfolio of risks as $S$.

They prove that an allocation $\{(Y_1, \ldots, Y_n): \sum_{i=1}^n Y_i = S = \sum_{i=1}^n X_i\}$ that is chosen to minimize $\sum_{i=1}^n RVaR_{\alpha_i, \beta_i} (S)$ is Pareto optimal. Moreover, under mild continuity assumptions , this allocation can be achieved by \[ \begin{array}{lll} Y_i &= S \times I\left( F^{-1}\left[1 - \sum_{k=1}^i \alpha_k\right] \le S \le F^{-1}\left[1 - \sum_{k=1}^{i-1} \alpha_k\right] \right) & i=1, \ldots, n-1 \\ Y_n &= S \times I\left( S \le F^{-1}\left[1 - \sum_{k=1}^{n-1} \alpha_k\right] \right) , \end{array} \] a type of layered stop-loss agreement.