clear all
use https://sscc.wisc.edu/~rdimond/pa871/salaries.dta2 Regression
An introduction to regression usually starts with drawing lines on a scatter plot, which is great as a motivator for the technique but makes something as simple as an indicator variable a strange special case. So we’re going to start with the simplest model possible.
Start a do file. We’ll play fast and loose and not keep a log, but do start with a clear all so it’s reproducible. Then load the example data set salaries (copy and paste highly recommended).
2.1 Constant-Only Model
What we have here is fictional data from 100,000 employees at a firm. Now suppose you were given this data, and then asked to guess the salary of an employee–but you were told absolutely nothing about them. Of course you aren’t expected to get their salary right; the goal is to be off by as little as possible.
The median or the mean value seem like good guesses. If we stipulate that the goal is to minimize the difference between your guess and the actual salary squared, then it’s possible to prove that the mean is the best guess. Find the mean with the sum command (salary is measured in thousands of dollars).
sum salary
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
salary | 100,000 67.65335 25.70563 21.11117 181.7357If you run a regression model for salary with no predictors, i.e. you don’t tell the model anything about the employees other than their salaries, it will make the exact same guess.
reg salary
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(0, 99999) = 0.00
Model | 0 0 . Prob > F = .
Residual | 66077289.3 99,999 660.7795 R-squared = 0.0000
-------------+---------------------------------- Adj R-squared = 0.0000
Total | 66077289.3 99,999 660.7795 Root MSE = 25.706
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_cons | 67.65335 .0812883 832.26 0.000 67.49402 67.81267
------------------------------------------------------------------------------The constant in this regression model is just the mean of salary, and since there are no other predictors that’s the predicted value of salary for all observations.
2.2 Indicator Variables
The firm has carried out a training program (in fact they’ve hired you to evaluate whether the program worked). Now suppose you’re told whether the employee completed the training program or not and asked to guess their salary. Assuming the training program had some impact on salary, a good guess for someone who completed the program would be the mean salary of all employees who completed the program, while a good guess for someone who did not complete the program would be the mean salary of all the employees who did not.
bysort train: sum salary
-------------------------------------------------------------------------------
-> train = Untrained
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
salary | 66,204 71.11991 27.31844 21.11117 181.7357
-------------------------------------------------------------------------------
-> train = Trained
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
salary | 33,796 60.86258 20.58193 25.54803 181.204
An alternative way to get the same numbers:
tab train, sum(salary)
| Summary of salary
train | Mean Std. dev. Freq.
------------+------------------------------------
Untrained | 71.119912 27.318445 66,204
Trained | 60.862584 20.58193 33,796
------------+------------------------------------
Total | 67.653345 25.705632 100,000(Things do not look good for this training program, but don’t pass judgment just yet.)
A regression that adds train as a predictor (more precisely, i.train since train is an indicator variable) will make the same guesses, but describe them in a different way.
reg salary i.train
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(1, 99998) = 3694.12
Model | 2354062.69 1 2354062.69 Prob > F = 0.0000
Residual | 63723226.6 99,998 637.245011 R-squared = 0.0356
-------------+---------------------------------- Adj R-squared = 0.0356
Total | 66077289.3 99,999 660.7795 Root MSE = 25.244
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | -10.25733 .1687635 -60.78 0.000 -10.5881 -9.926554
_cons | 71.11991 .0981095 724.90 0.000 70.92762 71.31221
------------------------------------------------------------------------------The constant is the mean of salary for untrained. The coefficent Trained is the difference between the two groups: 71.11991 - 10.25733 = 60.86258, the mean salary of the employees who completed the training. This allows you to test the hypothesis that the mean of salary is different for the two groups just by looking at the p-value on Trained. In fact, it’s equivalent to running a t-test.
ttest salary, by(train)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. err. Std. dev. [95% conf. interval]
---------+--------------------------------------------------------------------
Untraine | 66,204 71.11991 .1061729 27.31844 70.91181 71.32801
Trained | 33,796 60.86258 .1119576 20.58193 60.64314 61.08202
---------+--------------------------------------------------------------------
Combined | 100,000 67.65335 .0812883 25.70563 67.49402 67.81267
---------+--------------------------------------------------------------------
diff | 10.25733 .1687635 9.926554 10.5881
------------------------------------------------------------------------------
diff = mean(Untraine) - mean(Trained) t = 60.7793
H0: diff = 0 Degrees of freedom = 99998
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 1.0000 Pr(|T| > |t|) = 0.0000 Pr(T > t) = 0.0000In this regression, the untrained are the reference group. The coefficient on Trained then tells you the difference between the trained group and the reference group (untrained).
But what if you want to know the predicted value of salary for the trained group based on the regression model? Do you have to do (gasp) math? Of course not. The margins command will do it for you:
margins train
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Untrained | 71.11991 .0981095 724.90 0.000 70.92762 71.31221
Trained | 60.86258 .1373158 443.23 0.000 60.59345 61.13172
------------------------------------------------------------------------------Those numbers are equal to the mean salaries of the two groups. But that’s not actually what margins does. Asked to calculate margins for train, which it knows is an indicator variable because you put i.train in your regression, it first sets everyone’s value of train to 0, calculates everyone’s predicted salary, and reports the mean. Then it sets everyone’s value of train to 0 and repeats the process. You’ll see why that’s important soon.
You can also ask margins to calculate the difference between the two groups with the dydx() option.
margins, dydx(train)
Conditional marginal effects Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
dy/dx wrt: 1.train
------------------------------------------------------------------------------
| Delta-method
| dy/dx std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | -10.25733 .1687635 -60.78 0.000 -10.5881 -9.926554
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.Since this is a linear model, the result is just the coefficient on Trained. But in more complicated models this can be very useful.
2.3 Categorical Variables
Now suppose that instead of train you know edu, the employee’s education level. It’s a categorical variable with 3 categories, or levels. Again, a good guess would be the mean salary for everyone with that level of education.
tab edu, sum(salary)
| Summary of salary
edu | Mean Std. dev. Freq.
------------+------------------------------------
High Scho | 43.56295 9.869016 32,972
Bachelor | 71.086272 9.2926206 57,481
Advanced | 130.18403 8.9240392 9,547
------------+------------------------------------
Total | 67.653345 25.705632 100,000And that’s what a regression will do too, but again it reports it in terms of a reference level and then differences from it.
reg salary i.edu
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(2, 99997) > 99999.00
Model | 57142209.4 2 28571104.7 Prob > F = 0.0000
Residual | 8935079.9 99,997 89.3534796 R-squared = 0.8648
-------------+---------------------------------- Adj R-squared = 0.8648
Total | 66077289.3 99,999 660.7795 Root MSE = 9.4527
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu |
Bachelor | 27.52332 .0653029 421.47 0.000 27.39533 27.65132
Advanced | 86.62108 .1098604 788.47 0.000 86.40575 86.8364
|
_cons | 43.56295 .0520575 836.82 0.000 43.46092 43.66498
------------------------------------------------------------------------------By default, Stata will use the lowest value as the reference. You can change that if you want to:
reg salary ib2.edu
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(2, 99997) > 99999.00
Model | 57142209.4 2 28571104.7 Prob > F = 0.0000
Residual | 8935079.9 99,997 89.3534796 R-squared = 0.8648
-------------+---------------------------------- Adj R-squared = 0.8648
Total | 66077289.3 99,999 660.7795 Root MSE = 9.4527
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu |
High School | -86.62108 .1098604 -788.47 0.000 -86.8364 -86.40575
Bachelor | -59.09775 .1044692 -565.70 0.000 -59.30251 -58.89299
|
_cons | 130.184 .0967436 1345.66 0.000 129.9944 130.3736
------------------------------------------------------------------------------Note how the effect of Advanced compared to the base level High School is just the negative of the effect of High School compared to the base level Advanced. These are fundamentally the same model (they give the same predicted values), just described differently.
margins works the same way as with an indicator, just with more levels to report.
margins edu
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu |
High School | 43.56295 .0520575 836.82 0.000 43.46092 43.66498
Bachelor | 71.08627 .039427 1802.99 0.000 71.009 71.16355
Advanced | 130.184 .0967436 1345.66 0.000 129.9944 130.3736
------------------------------------------------------------------------------margins, dydx(edu)
Conditional marginal effects Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
dy/dx wrt: 0.edu 1.edu
------------------------------------------------------------------------------
| Delta-method
| dy/dx std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu |
High School | -86.62108 .1098604 -788.47 0.000 -86.8364 -86.40575
Bachelor | -59.09775 .1044692 -565.70 0.000 -59.30251 -58.89299
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.2.4 Categorical Interactions
Now suppose you know both train and edu so your guess will be the mean value for people with the same level of both variables.
tab edu train, sum(salary)
Means, Standard Deviations and Frequencies of salary
| train
edu | Untrained Trained | Total
-----------+----------------------+----------
High Scho | 41.589563 45.510414 | 43.56295
| 9.7972257 9.547799 | 9.869016
| 16377 16595 | 32972
-----------+----------------------+----------
Bachelor | 70.86273 71.665069 | 71.086272
| 9.3972106 8.9906781 | 9.2926206
| 41466 16015 | 57481
-----------+----------------------+----------
Advanced | 130.23758 129.80647 | 130.18403
| 8.9427914 8.7851637 | 8.9240392
| 8361 1186 | 9547
-----------+----------------------+----------
Total | 71.119912 60.862584 | 67.653345
| 27.318445 20.58193 | 25.705632
| 66204 33796 | 100000Or if you’d prefer a simpler table, use table instead of tabulate.
table (edu) (train), stat(mean salary) nototal
-------------------------------------
| train
| Untrained Trained
--------------+----------------------
edu |
High School | 41.58956 45.51041
Bachelor | 70.86273 71.66507
Advanced | 130.2376 129.8065
-------------------------------------Note how the difference between the trained and untrained is different for each education level. To allow this in a regression model, we need to include an interaction between train and edu in the predictors. Putting ## between two variables means to include both the variables alone (their main effect) and the interaction between them. # between two variables refers to just the interaction. Variables in interactions are assumed to be factor variables, so we don’t need to put i. before them.
reg salary train##edu
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(5, 99994) > 99999.00
Model | 57276554.4 5 11455310.9 Prob > F = 0.0000
Residual | 8800734.89 99,994 88.0126297 R-squared = 0.8668
-------------+---------------------------------- Adj R-squared = 0.8668
Total | 66077289.3 99,999 660.7795 Root MSE = 9.3815
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | 3.920852 .1033331 37.94 0.000 3.71832 4.123383
|
edu |
Bachelor | 29.27317 .0865834 338.09 0.000 29.10346 29.44287
Advanced | 88.64802 .1260981 703.01 0.000 88.40087 88.89517
|
train#edu |
Trained #|
Bachelor | -3.118512 .1352623 -23.06 0.000 -3.383625 -2.8534
Trained #|
Advanced | -4.351964 .3088915 -14.09 0.000 -4.957387 -3.74654
|
_cons | 41.58956 .0733087 567.32 0.000 41.44588 41.73325
------------------------------------------------------------------------------Now Trained is the effect of training for the base category of edu, High School. Meanwhile Bachelor and Advanced is the effect of edu for the base category of train, which is Untrained. The interaction terms Trained#Bachelor and Trained#Advanced are the additional effect to be added if someone is both trained and has that level of education.
This looks confusing, but if you have margins add it all up you’ll see it’s still just the means.
margins edu#train
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu#train |
High School #|
Untrained | 41.58956 .0733087 567.32 0.000 41.44588 41.73325
High School #|
Trained | 45.51041 .0728256 624.92 0.000 45.36768 45.65315
Bachelor #|
Untrained | 70.86273 .0460709 1538.12 0.000 70.77243 70.95303
Bachelor #|
Trained | 71.66507 .0741326 966.72 0.000 71.51977 71.81037
Advanced #|
Untrained | 130.2376 .1025991 1269.38 0.000 130.0365 130.4387
Advanced #|
Trained | 129.8065 .2724145 476.50 0.000 129.2725 130.3404
------------------------------------------------------------------------------marginsplot automatically makes a data visualization out of these numbers.
marginsplot
Variables that uniquely identify margins: edu train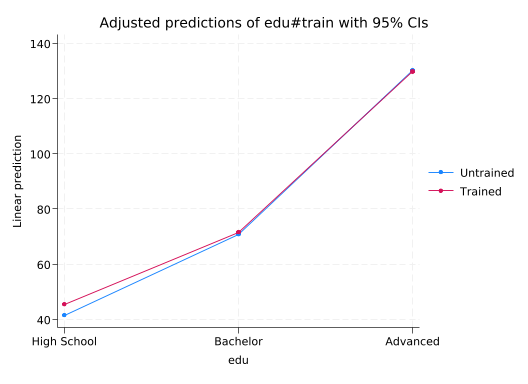
We can also ask margins to add up the total effect of train at each level of edu.
margins edu, dydx(train)
Conditional marginal effects Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
dy/dx wrt: 1.train
------------------------------------------------------------------------------
| Delta-method
| dy/dx std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
0.train | (base outcome)
-------------+----------------------------------------------------------------
1.train |
edu |
High School | 3.920852 .1033331 37.94 0.000 3.71832 4.123383
Bachelor | .8023392 .0872821 9.19 0.000 .6312674 .973411
Advanced | -.4311121 .2910948 -1.48 0.139 -1.001654 .1394302
------------------------------------------------------------------------------
Note: dy/dx for factor levels is the discrete change from the base level.2.5 Categorical Variables Without Interactions
It’s uncommon to be able to reliably estimate interactions like that–most data sets have fewer than the 100,000 observations we’ve been using. So we commonly assume variables have the same effect for all observations.
reg salary i.edu i.train
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(3, 99996) > 99999.00
Model | 57223444.8 3 19074481.6 Prob > F = 0.0000
Residual | 8853844.46 99,996 88.5419863 R-squared = 0.8660
-------------+---------------------------------- Adj R-squared = 0.8660
Total | 66077289.3 99,999 660.7795 Root MSE = 9.4097
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu |
Bachelor | 27.967 .0666356 419.70 0.000 27.8364 28.09761
Advanced | 87.36961 .1121178 779.27 0.000 87.14986 87.58936
|
train |
Trained | 1.974619 .0651906 30.29 0.000 1.846846 2.102392
_cons | 42.56911 .0613345 694.05 0.000 42.4489 42.68933
------------------------------------------------------------------------------The mean predicted salaries no longer line up exactly with the observed means.
table (edu) (train), stat(mean salary) nototal
margins edu#train
-------------------------------------
| train
| Untrained Trained
--------------+----------------------
edu |
High School | 41.58956 45.51041
Bachelor | 70.86273 71.66507
Advanced | 130.2376 129.8065
-------------------------------------
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
edu#train |
High School #|
Untrained | 42.56911 .0613345 694.05 0.000 42.4489 42.68933
High School #|
Trained | 44.54373 .061105 728.97 0.000 44.42397 44.6635
Bachelor #|
Untrained | 70.53612 .0432466 1631.02 0.000 70.45135 70.62088
Bachelor #|
Trained | 72.51074 .0612533 1183.79 0.000 72.39068 72.63079
Advanced #|
Untrained | 129.9387 .0966432 1344.52 0.000 129.7493 130.1281
Advanced #|
Trained | 131.9133 .1119546 1178.27 0.000 131.6939 132.1328
------------------------------------------------------------------------------marginsplot makes it easy to see the difference between this model and the previous one.
marginsplot
Variables that uniquely identify margins: edu train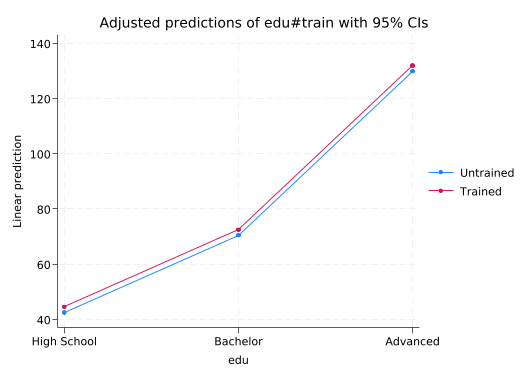
2.5.1 Continuous Predictors
Now suppose we know the tenure (years worked at the company, not “has tenure” like in academia) of each employee, a continuous variable. Now we’ve finally gotten to drawing lines on scatterplots.
scatter salary tenure, msize(tiny) || lfit salary tenure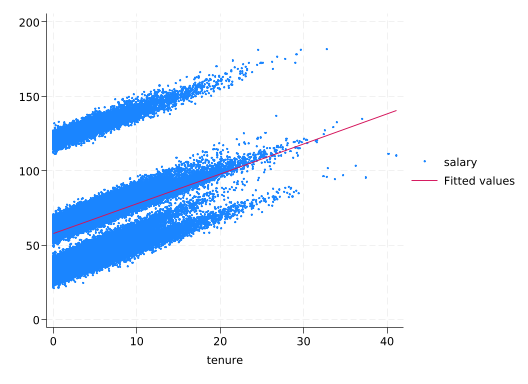
regress will estimate the slope of that line.
regress salary tenure
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(1, 99998) = 12321.47
Model | 7248691.6 1 7248691.6 Prob > F = 0.0000
Residual | 58828597.7 99,998 588.297743 R-squared = 0.1097
-------------+---------------------------------- Adj R-squared = 0.1097
Total | 66077289.3 99,999 660.7795 Root MSE = 24.255
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
tenure | 2.009571 .0181039 111.00 0.000 1.974088 2.045055
_cons | 57.62375 .11852 486.19 0.000 57.39145 57.85605
------------------------------------------------------------------------------This means the predicted starting salary is \$57.6k and salaries increase by \$2k for every year of tenure.
But we know edu makes a big difference, so add it to the model.
reg salary tenure i.edu
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(3, 99996) > 99999.00
Model | 64476272.6 3 21492090.9 Prob > F = 0.0000
Residual | 1601016.69 99,996 16.0108073 R-squared = 0.9758
-------------+---------------------------------- Adj R-squared = 0.9758
Total | 66077289.3 99,999 660.7795 Root MSE = 4.0014
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
tenure | 2.021376 .0029866 676.81 0.000 2.015522 2.02723
|
edu |
Bachelor | 27.5267 .0276429 995.80 0.000 27.47252 27.58088
Advanced | 86.69164 .0465043 1864.16 0.000 86.60049 86.78278
|
_cons | 33.46576 .0266113 1257.58 0.000 33.4136 33.51792
------------------------------------------------------------------------------Salaries still go up by about \$2k/year, but the expected starting salary depends on education: \$33.5k for high school, plus \$27.5k for a Bachelor’s, or \$86.7k for an advanced degree. margins and marginsplot can be really useful here, but since tenure is continuous we need the at() option to specify the values we’re interested in.
margins edu, at(tenure=(0(5)20))
marginsplot, addplot(scatter salary tenure, below)
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: tenure = 0
2._at: tenure = 5
3._at: tenure = 10
4._at: tenure = 15
5._at: tenure = 20
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_at#edu |
1 #|
High School | 33.46576 .0266113 1257.58 0.000 33.4136 33.51792
1#Bachelor | 60.99246 .0223822 2725.04 0.000 60.94859 61.03633
1#Advanced | 120.1574 .0435491 2759.13 0.000 120.072 120.2428
2 #|
High School | 43.57264 .0220361 1977.33 0.000 43.52945 43.61583
2#Bachelor | 71.09934 .0166896 4260.11 0.000 71.06663 71.13205
2#Advanced | 130.2643 .040952 3180.90 0.000 130.184 130.3445
3 #|
High School | 53.67952 .0266273 2015.96 0.000 53.62733 53.73171
3#Bachelor | 81.20622 .022408 3623.99 0.000 81.1623 81.25014
3#Advanced | 140.3712 .0436303 3217.28 0.000 140.2856 140.4567
4 #|
High School | 63.7864 .0371273 1718.04 0.000 63.71363 63.85917
4#Bachelor | 91.3131 .03423 2667.64 0.000 91.24601 91.38019
4#Advanced | 150.478 .0507557 2964.75 0.000 150.3786 150.5775
5 #|
High School | 73.89328 .0499386 1479.68 0.000 73.7954 73.99116
5#Bachelor | 101.42 .0478253 2120.63 0.000 101.3262 101.5137
5#Advanced | 160.5849 .0607839 2641.90 0.000 160.4658 160.7041
------------------------------------------------------------------------------
Variables that uniquely identify margins: tenure edu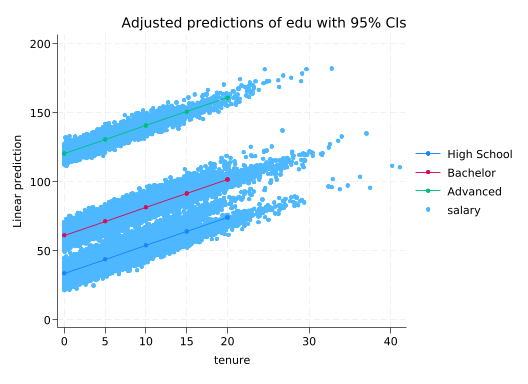
2.6 Interactions With Continuous Variables
Now let’s look at how training affects the relationship between tenure and salary.
scatter salary tenure, colorvar(train) colordisc msize(tiny) coloruseplegend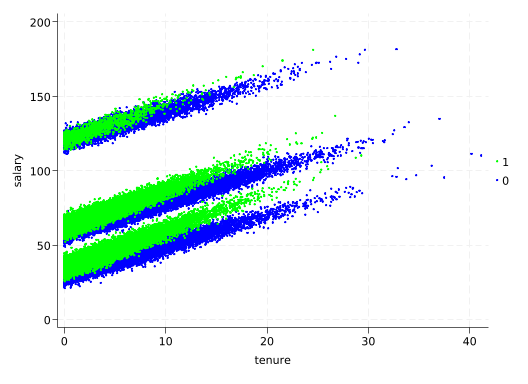
The slope of the tenure line is different for trained employees than for untrained employees! This again calls for an interaction in the regression model. Remember that Stata assumes variables in interactions are factor variables, so we need to put c. in front of tenure to specify that it is continuous.
reg salary train##c.tenure
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(3, 99996) = 4980.77
Model | 8590233.06 3 2863411.02 Prob > F = 0.0000
Residual | 57487056.2 99,996 574.893558 R-squared = 0.1300
-------------+---------------------------------- Adj R-squared = 0.1300
Total | 66077289.3 99,999 660.7795 Root MSE = 23.977
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | -9.979142 .2475621 -40.31 0.000 -10.46436 -9.493924
tenure | 1.743132 .0207497 84.01 0.000 1.702463 1.783801
|
train#|
c.tenure |
Trained | .5530884 .0426809 12.96 0.000 .4694344 .6367424
|
_cons | 61.57144 .1469786 418.91 0.000 61.28336 61.85952
------------------------------------------------------------------------------This suggests Trained people have lower starting salaries by about \$10k, but while salaries for Untrained people go up by \$1.7k/year of tenure, salaries for trained people go up by \$2.3k/year of tenure (1.743132 + .5530884). margins will make it easy to see the overall effect.
margins train, at(tenure=(0(5)20))
marginsplot
Adjusted predictions Number of obs = 100,000
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: tenure = 0
2._at: tenure = 5
3._at: tenure = 10
4._at: tenure = 15
5._at: tenure = 20
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_at#train |
1#Untrained | 61.57144 .1469786 418.91 0.000 61.28336 61.85952
1#Trained | 51.5923 .1992091 258.99 0.000 51.20185 51.98274
2#Untrained | 70.2871 .093712 750.03 0.000 70.10342 70.47077
2#Trained | 63.0734 .1352784 466.25 0.000 62.80825 63.33854
3#Untrained | 79.00276 .1322446 597.40 0.000 78.74356 79.26195
3#Trained | 74.5545 .2578209 289.17 0.000 74.04917 75.05982
4#Untrained | 87.71842 .2184555 401.54 0.000 87.29025 88.14659
4#Trained | 86.0356 .4291834 200.46 0.000 85.19441 86.87679
5#Untrained | 96.43407 .3154115 305.74 0.000 95.81587 97.05228
5#Trained | 97.5167 .609492 160.00 0.000 96.3221 98.7113
------------------------------------------------------------------------------
Variables that uniquely identify margins: tenure train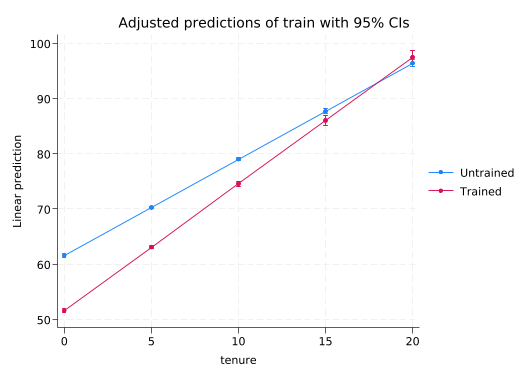
2.7 The Complete Model
But why would a training program reduce starting salaries? Well, let’s look at who gets trained.
tab edu train, row
+----------------+
| Key |
|----------------|
| frequency |
| row percentage |
+----------------+
| train
edu | Untrained Trained | Total
------------+----------------------+----------
High School | 16,377 16,595 | 32,972
| 49.67 50.33 | 100.00
------------+----------------------+----------
Bachelor | 41,466 16,015 | 57,481
| 72.14 27.86 | 100.00
------------+----------------------+----------
Advanced | 8,361 1,186 | 9,547
| 87.58 12.42 | 100.00
------------+----------------------+----------
Total | 66,204 33,796 | 100,000
| 66.20 33.80 | 100.00 About half of employees with a high school education get trained, but only 28% of those with a Bachelor’s degree and 12% of those with an advanced degree. Given the very strong relationship between edu and salary, trying to estimate the effect of train on salary without controlling for edu is going to be a disaster. We also saw evidence that the effect of train depends on edu, and the effect of tenure depends on train, so we’ll include both interactions.
regress salary train##(c.tenure i.edu)
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(7, 99992) > 99999.00
Model | 65176547.2 7 9310935.32 Prob > F = 0.0000
Residual | 900742.041 99,992 9.00814106 R-squared = 0.9864
-------------+---------------------------------- Adj R-squared = 0.9864
Total | 66077289.3 99,999 660.7795 Root MSE = 3.0014
------------------------------------------------------------------------------
salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | 4.930425 .0413136 119.34 0.000 4.849451 5.011399
tenure | 1.996295 .0026001 767.76 0.000 1.991199 2.001392
|
edu |
Bachelor | 29.99815 .0277161 1082.34 0.000 29.94383 30.05247
Advanced | 90.00605 .0403804 2228.95 0.000 89.9269 90.0852
|
train#|
c.tenure |
Trained | .5101078 .0053488 95.37 0.000 .4996242 .5205914
|
train#edu |
Trained #|
Bachelor | -2.98867 .0433131 -69.00 0.000 -3.073563 -2.903776
Trained #|
Advanced | -4.930725 .0988479 -49.88 0.000 -5.124465 -4.736984
|
_cons | 30.02873 .0278709 1077.42 0.000 29.9741 30.08335
------------------------------------------------------------------------------With an R-squared of .986 and coefficients that are extremely close to round numbers, you can tell this is 1) made-up data and 2) a model that matches the data-generating process.
marginsplot can make this easy to understand (I’ll omit the margins output for convenience).
quietly margins edu#train, at(tenure=(0(5)20))
marginsplot
Variables that uniquely identify margins: tenure edu train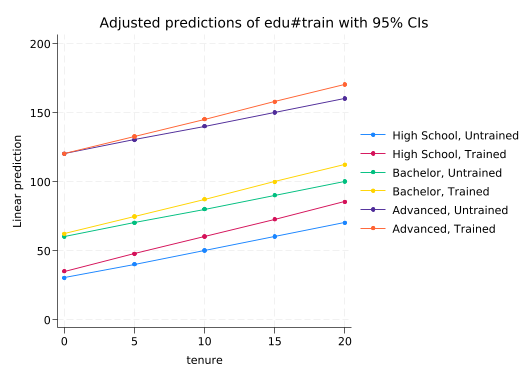
And the effect of train?
quietly margins edu, dydx(train) at(tenure=(0(5)20))
marginsplot
Variables that uniquely identify margins: tenure edu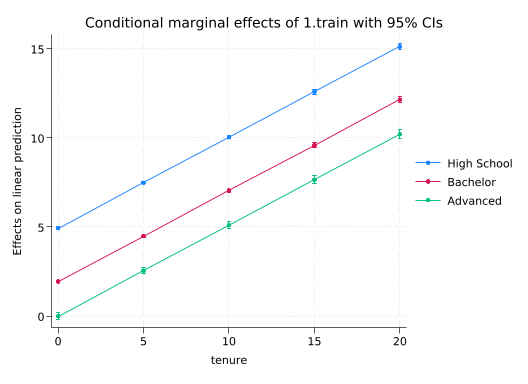
For those with advanced degrees, train only has an effect via tenure. But for those with less education, it has both an effect on its own and the effect through tenure. Note that we did not include a three-way interaction between train, edu, and tenure so the increase in the effect of tenure associated with train is the same for all levels of edu.
2.8 Diagnostics
Before we trust this model we should do at least some regression diagnostics. But the right diagnostics.
salary is not remotely normal–like most salary distributions, it is right-skewed.
sum salary, detail
hist salary
salary
-------------------------------------------------------------
Percentiles Smallest
1% 29.5404 21.11117
5% 34.22136 21.49281
10% 37.6162 21.52696 Obs 100,000
25% 49.12166 22.31187 Sum of wgt. 100,000
50% 65.60289 Mean 67.65335
Largest Std. dev. 25.70563
75% 75.53474 178.1305
90% 101.6421 181.204 Variance 660.7795
95% 127.9607 181.3195 Skewness 1.13581
99% 141.6542 181.7357 Kurtosis 4.343584
(bin=50, start=21.111168, width=3.2124898)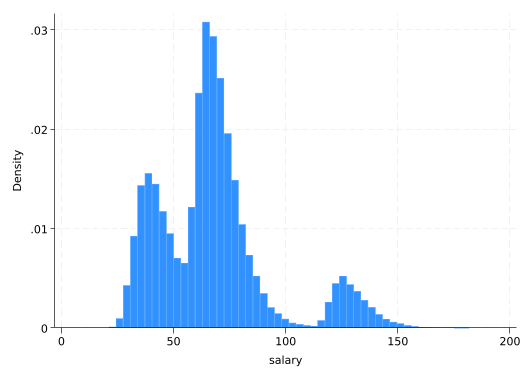
Is that a problem? Should we be using a log transform to make it more normal? No. OLS regression does not require that the outcome variable be normally distributed; it requires that the residuals be normally distributed. You can calculate the residuals with the predict command and residual option.
predict residuals, residualNow look at their distribution.
hist residuals(bin=50, start=-12.927955, width=.50254992)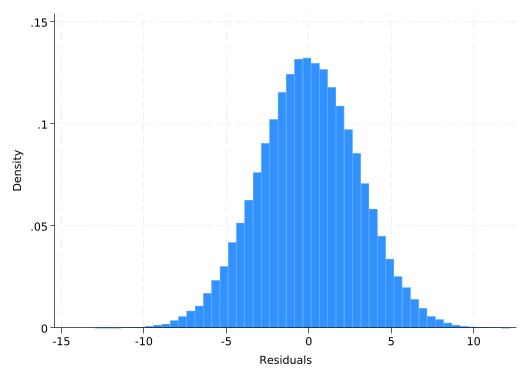
qnorm residuals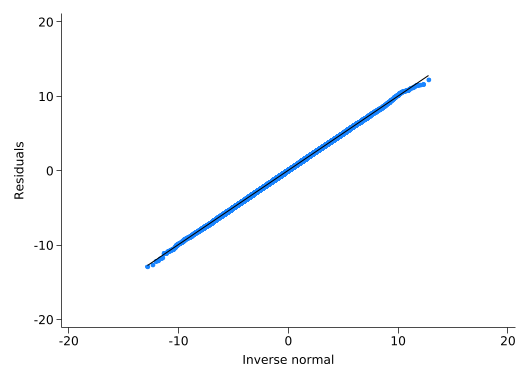
That’s more normal than you’ll ever see with real data. The model successfully explained all the non-normal components of salary.
A right-skewed distribution can suggest your data-generating process is multiplicative: if you add a bunch of random numbers the result will be normal, but if you multiply a bunch of random numbers the result will be log-normal, which is right-skewed. Taking the log will make a multiplicative process additive and a good candidate for a linear model. But check the residuals themselves before you assume such a process.
Residuals should be independent of both the predicted (or fitted) values and the continuous predictors. If you see a relationship between them, then that suggests there’s something wrong or missing in your model. rvfplot (residuals vs fitted values) will get the first, scatter will get you the rest.
rvfplot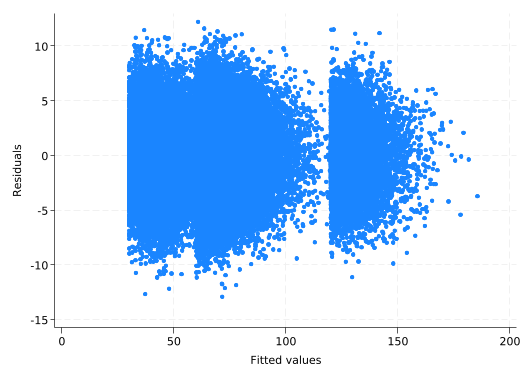
The residuals should always be centered around zero. Don’t be fooled by the fact that areas with lots of points will have more outliers.
scatter res tenure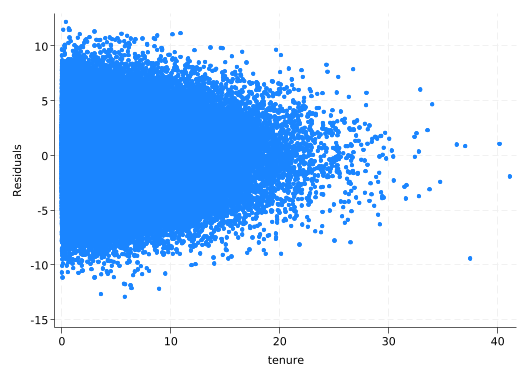
What would it look like if we did a log transform?
gen log_salary = ln(salary)reg log_salary train##(c.tenure i.edu)
quietly margins edu#train, at(tenure=(0(5)20)) expression(exp(predict(xb)))
marginsplot
Source | SS df MS Number of obs = 100,000
-------------+---------------------------------- F(7, 99992) > 99999.00
Model | 12801.2091 7 1828.74416 Prob > F = 0.0000
Residual | 473.811329 99,992 .004738492 R-squared = 0.9643
-------------+---------------------------------- Adj R-squared = 0.9643
Total | 13275.0205 99,999 .132751532 Root MSE = .06884
------------------------------------------------------------------------------
log_salary | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
train |
Trained | .0934263 .0009475 98.60 0.000 .0915692 .0952835
tenure | .029955 .0000596 502.31 0.000 .0298381 .0300719
|
edu |
Bachelor | .5610196 .0006357 882.56 0.000 .5597737 .5622655
Advanced | 1.185096 .0009261 1279.62 0.000 1.183281 1.186911
|
train#|
c.tenure |
Trained | .0117355 .0001227 95.66 0.000 .011495 .0119759
|
train#edu |
Trained #|
Bachelor | -.0799929 .0009934 -80.52 0.000 -.0819399 -.0780459
Trained #|
Advanced | -.1061102 .0022671 -46.80 0.000 -.1105536 -.1016667
|
_cons | 3.528906 .0006392 5520.61 0.000 3.527653 3.530158
------------------------------------------------------------------------------
Variables that uniquely identify margins: tenure edu train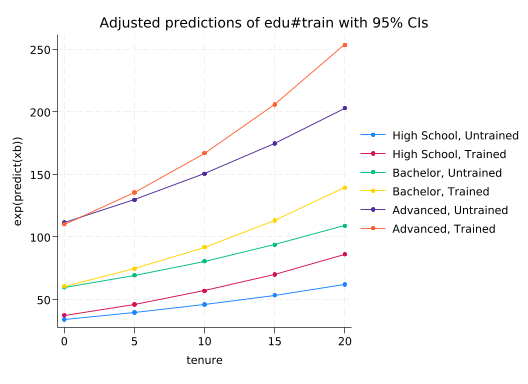
Assuming a log-linear form introduced a curve into our model even though there’s no curve in the data. The model will fit it as best it can, but the curved line will be too high at the right and left ends and too low in the middle. Thus the residuals will be negative on the right and left ends and positive in the middle. You can see that with rvfplot.
rvfplot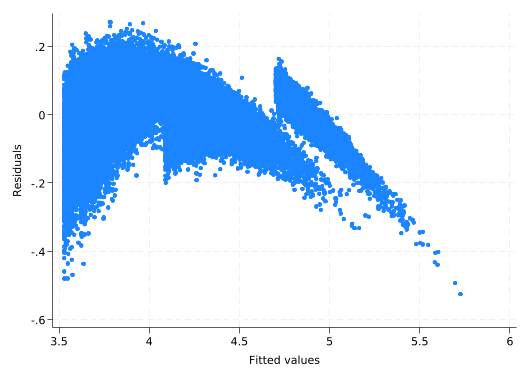
On the other hand, if this data really were log-linear, you’d see the same sort of pattern if you tried to use a linear model. Similar plots could also lead you to include squared terms in your model (a squared term is a second order Taylor series approximation to anything).
2.9 Why You Shouldn’t Use Interactions Lightly
Interactions are hard to estimate–you need some combination of a lot of data, a strong effect, and not much noise. This data set is bigger than you’re likely to work with in the real world, and has a far higher R-squared (i.e. there’s very little noise). The salary2 and train2 variables are more like what you’re likely to actually see. salary2 is a lot less predictable (in the real world we’re lucky to be able to predict 20% of the variation in salaries) and it only has 800 observations. On the other hand, to make things easier train2 is completely random and has a main effect on all education levels so it’s easier to estimate.
Start with a simple model where we assume training has the same effect for everyone.
reg salary2 i.train2 tenure i.edu
Source | SS df MS Number of obs = 800
-------------+---------------------------------- F(4, 795) = 95.50
Model | 666617.082 4 166654.271 Prob > F = 0.0000
Residual | 1387311.37 795 1745.04575 R-squared = 0.3246
-------------+---------------------------------- Adj R-squared = 0.3212
Total | 2053928.45 799 2570.62385 Root MSE = 41.774
------------------------------------------------------------------------------
salary2 | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
1.train2 | 6.986803 3.263948 2.14 0.033 .579828 13.39378
tenure | 2.290322 .3580977 6.40 0.000 1.587394 2.993251
|
edu |
Bachelor | 34.40527 3.219203 10.69 0.000 28.08612 40.72441
Advanced | 98.55754 5.490826 17.95 0.000 87.77931 109.3358
|
_cons | 24.58744 3.220637 7.63 0.000 18.26548 30.9094
------------------------------------------------------------------------------Great, training has an effect. Now try interacting train2 with everything like we did before.
reg salary2 i.train2##(c.tenure i.edu)
Source | SS df MS Number of obs = 800
-------------+---------------------------------- F(7, 792) = 54.87
Model | 670792.162 7 95827.4518 Prob > F = 0.0000
Residual | 1383136.29 792 1746.38421 R-squared = 0.3266
-------------+---------------------------------- Adj R-squared = 0.3206
Total | 2053928.45 799 2570.62385 Root MSE = 41.79
------------------------------------------------------------------------------
salary2 | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
1.train2 | 5.483388 6.972496 0.79 0.432 -8.203369 19.17014
tenure | 1.959505 .4406548 4.45 0.000 1.094516 2.824495
|
edu |
Bachelor | 36.04839 3.783965 9.53 0.000 28.6206 43.47618
Advanced | 97.90354 6.464464 15.14 0.000 85.21403 110.593
|
train2#|
c.tenure |
1 | .9428405 .7580626 1.24 0.214 -.545209 2.43089
|
train2#edu |
1#Bachelor | -5.31276 7.223985 -0.74 0.462 -19.49318 8.867661
1#Advanced | 2.261653 12.26855 0.18 0.854 -21.82107 26.34438
|
_cons | 25.34002 3.644351 6.95 0.000 18.18629 32.49375
------------------------------------------------------------------------------Now training has no effect! Since I made the data, I can tell you the effect of train2 does vary with edu and tenure. This is the “right” model in that sense. But it gives you the wrong answer to the question you care about “Does training increase salaries?” The model doesn’t have enough information to precisely estimate all the different ways train2 affects salary2, so they all have large standard errors and are not significantly different from zero. Don’t try to estimate a more complicated model than your data will support, even if you think it’s “right.”
All models are wrong; some models are useful.