clear all
use https://sscc.wisc.edu/~rdimond/pa871/gapminder.dta3 Fixed Effects
The Gapminder data contains data on countries over time. This extract contains life expectancy (life_exp) and GDP per-capita (gdp_pcap).
Cut down the sample to just 1970-2023. Also, we’re going to need a numeric code for countries rather than a string name. Finally, convert gdp_pcap to thousands of dollars just for convenience. (Interestingly, one of the later models will have convergence issues if you leave it alone or make it thousands of dollars.)
keep if year >1970 & year<2024
encode country, gen(cnum)
replace gdp_pcap = gdp_pcap/100000(48,360 observations deleted)
(10,335 real changes made)So what does the relationship between life_exp and gdp_pcap look like?
scatter life_exp gdp_pcap if cnum<=10, colorvar(cnum) colordiscrete coloruseplegend zlabel(, valuelabel)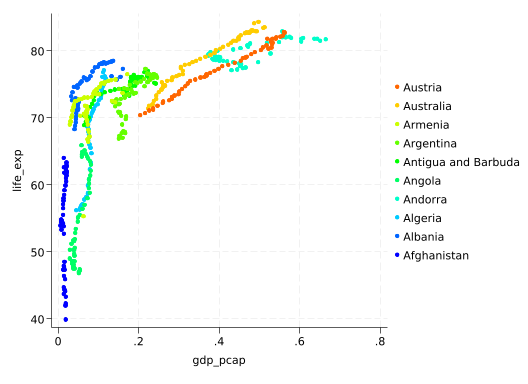
So…positive. Sort of. But the countries sure are different.
Run a regression and see what it looks like.
reg life_exp gdp_pcap
Source | SS df MS Number of obs = 10,335
-------------+---------------------------------- F(1, 10333) = 4621.53
Model | 285744.911 1 285744.911 Prob > F = 0.0000
Residual | 638880.396 10,333 61.8291296 R-squared = 0.3090
-------------+---------------------------------- Adj R-squared = 0.3090
Total | 924625.307 10,334 89.4740959 Root MSE = 7.8632
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
gdp_pcap | 26.39623 .3882838 67.98 0.000 25.63512 27.15734
_cons | 63.25835 .0977924 646.86 0.000 63.06666 63.45004
------------------------------------------------------------------------------This ignores the differences between countries. So let’s instead treat country, or rather cnum, as a categorical variable.
reg life_exp gdp_pcap i.cnum
Source | SS df MS Number of obs = 10,335
-------------+---------------------------------- F(195, 10139) = 183.11
Model | 720137.404 195 3693.01233 Prob > F = 0.0000
Residual | 204487.903 10,139 20.1684488 R-squared = 0.7788
-------------+---------------------------------- Adj R-squared = 0.7746
Total | 924625.307 10,334 89.4740959 Root MSE = 4.4909
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
gdp_pcap | 18.86835 .5390142 35.01 0.000 17.81178 19.92493
|
cnum |
Albania | 19.39616 .8729709 22.22 0.000 17.68497 21.10736
Algeria | 13.14916 .8732918 15.06 0.000 11.43734 14.86099
Andorra | 17.27633 .908471 19.02 0.000 15.49555 19.05712
Angola | -.4278586 .872618 -0.49 0.624 -2.138363 1.282645
Antigua a.. | 17.56298 .8757965 20.05 0.000 15.84625 19.27972
Argentina | 16.01975 .8771466 18.26 0.000 14.30037 17.73913
Armenia | 16.42532 .8730826 18.81 0.000 14.7139 18.13673
Australia | 18.13644 .8923288 20.32 0.000 16.3873 19.88559
Austria | 16.0544 .8975558 17.89 0.000 14.29502 17.81379
Azerbaijan | 11.62727 .8733604 13.31 0.000 9.91531 13.33923
Bahamas | 11.56921 .8883778 13.02 0.000 9.827816 13.31061
Bahrain | 11.554 .8900366 12.98 0.000 9.809356 13.29865
Bangladesh | 8.483651 .8724142 9.72 0.000 6.773547 10.19376
Barbados | 18.04195 .87508 20.62 0.000 16.32662 19.75728
Belarus | 15.33128 .8741717 17.54 0.000 13.61773 17.04483
Belgium | 16.38781 .8948216 18.31 0.000 14.63378 18.14183
Belize | 17.23134 .8729014 19.74 0.000 15.52028 18.9424
Benin | 3.202591 .8724096 3.67 0.000 1.492496 4.912687
Bhutan | 8.797312 .8725871 10.08 0.000 7.086868 10.50776
Bolivia | 9.200655 .8726885 10.54 0.000 7.490012 10.9113
Bosnia an.. | 18.03892 .872885 20.67 0.000 16.32789 19.74995
Botswana | 1.835705 .8734002 2.10 0.036 .1236678 3.547742
Brazil | 13.08272 .8740693 14.97 0.000 11.36937 14.79607
Brunei | 1.922189 .9727198 1.98 0.048 .0154661 3.828913
Bulgaria | 14.86513 .8750536 16.99 0.000 13.14985 16.5804
Burkina F.. | -.6780773 .8723955 -0.78 0.437 -2.388145 1.031991
Burundi | -2.461115 .8724006 -2.82 0.005 -4.171193 -.7510374
Cambodia | 3.287071 .872403 3.77 0.000 1.576988 4.997153
Cameroon | 2.964247 .8724363 3.40 0.001 1.254099 4.674395
Canada | 17.81294 .8943288 19.92 0.000 16.05988 19.566
Cape Verde | 15.3489 .8724913 17.59 0.000 13.63864 17.05916
Central A.. | -5.880191 .872398 -6.74 0.000 -7.590264 -4.170118
Chad | .1890434 .8723968 0.22 0.828 -1.521027 1.899114
Chile | 18.08641 .8755706 20.66 0.000 16.37012 19.8027
China | 15.74169 .8726819 18.04 0.000 14.03106 17.45232
Colombia | 17.86682 .873571 20.45 0.000 16.15444 19.57919
Comoros | 6.702306 .8724112 7.68 0.000 4.992207 8.412405
Congo, De.. | 2.131154 .8723966 2.44 0.015 .4210843 3.841225
Congo, Rep. | 1.816467 .872516 2.08 0.037 .1061632 3.526771
Costa Rica | 21.0186 .8745875 24.03 0.000 19.30424 22.73297
Cote d'Iv.. | 1.937685 .8725114 2.22 0.026 .2273901 3.64798
Croatia | 16.5767 .8783942 18.87 0.000 14.85488 18.29853
Cuba | 21.24426 .8728781 24.34 0.000 19.53325 22.95527
Cyprus | 16.78551 .8829116 19.01 0.000 15.05483 18.51619
Czech Rep.. | 16.11737 .8818614 18.28 0.000 14.38875 17.846
Denmark | 15.47935 .9003346 17.19 0.000 13.71451 17.24418
Djibouti | 7.526435 .8725122 8.63 0.000 5.816139 9.236732
Dominica | 16.52168 .8730996 18.92 0.000 14.81024 18.23313
Dominican.. | 16.20908 .873403 18.56 0.000 14.49703 17.92112
Ecuador | 16.3424 .8733153 18.71 0.000 14.63053 18.05427
Egypt | 9.69424 .8729553 11.11 0.000 7.983075 11.40541
El Salvador | 15.09848 .8727882 17.30 0.000 13.38764 16.80932
Equatoria.. | .4751035 .8741675 0.54 0.587 -1.238438 2.188645
Eritrea | -1.33172 .8723953 -1.53 0.127 -3.041788 .3783475
Estonia | 14.73725 .8792051 16.76 0.000 13.01384 16.46067
Eswatini | -.306678 .872661 -0.35 0.725 -2.017266 1.40391
Ethiopia | -.1173925 .8723975 -0.13 0.893 -1.827464 1.592679
Fiji | 11.6057 .8732437 13.29 0.000 9.893966 13.31743
Finland | 17.07628 .8914533 19.16 0.000 15.32886 18.82371
France | 18.20174 .8915811 20.42 0.000 16.45406 19.94941
Gabon | 4.746185 .8751855 5.42 0.000 3.030648 6.461722
Gambia | 7.488602 .872399 8.58 0.000 5.778528 9.198677
Georgia | 14.5995 .8736011 16.71 0.000 12.88707 16.31193
Germany | 16.21532 .8953816 18.11 0.000 14.4602 17.97045
Ghana | 6.020424 .8724385 6.90 0.000 4.310271 7.730576
Greece | 19.60723 .8819433 22.23 0.000 17.87844 21.33601
Grenada | 15.644 .8734728 17.91 0.000 13.93182 17.35618
Guatemala | 9.165264 .8728548 10.50 0.000 7.454296 10.87623
Guinea | -.5698511 .8723956 -0.65 0.514 -2.279919 1.140217
Guinea-Bi~u | -2.890927 .8723963 -3.31 0.001 -4.600996 -1.180857
Guyana | 8.590709 .873282 9.84 0.000 6.878904 10.30251
Haiti | 1.828114 .8724284 2.10 0.036 .1179817 3.538247
Honduras | 14.11227 .872518 16.17 0.000 12.40196 15.82257
Hong Kong.. | 12.64228 .8920455 14.17 0.000 10.8937 14.39087
Hungary | 14.60294 .8780538 16.63 0.000 12.88178 16.3241
Iceland | 18.79813 .8956019 20.99 0.000 17.04257 20.55368
India | 7.502909 .8724376 8.60 0.000 5.792758 9.213059
Indonesia | 10.36149 .8727605 11.87 0.000 8.650709 12.07228
Iran | 14.17784 .8742668 16.22 0.000 12.46411 15.89158
Iraq | 12.37067 .8729857 14.17 0.000 10.65945 14.0819
Ireland | 15.10982 .9009487 16.77 0.000 13.34378 16.87586
Israel | 19.27984 .8841218 21.81 0.000 17.54679 21.01289
Italy | 18.24812 .8915413 20.47 0.000 16.50053 19.99572
Jamaica | 19.35824 .8732728 22.17 0.000 17.64646 21.07003
Japan | 20.69271 .8885569 23.29 0.000 18.95096 22.43445
Jordan | 16.91762 .873333 19.37 0.000 15.20572 18.62953
Kazakhstan | 10.49616 .8759618 11.98 0.000 8.779101 12.21322
Kenya | 6.640893 .8724465 7.61 0.000 4.930725 8.351061
Kiribati | 2.480839 .8724181 2.84 0.004 .7707264 4.190951
Kuwait | 13.64699 .9138748 14.93 0.000 11.85561 15.43836
Kyrgyz Re.. | 12.91202 .8725633 14.80 0.000 11.20162 14.62241
Lao | 2.818108 .8724544 3.23 0.001 1.107925 4.528292
Latvia | 14.19163 .8772192 16.18 0.000 12.47211 15.91115
Lebanon | 15.35477 .8742995 17.56 0.000 13.64097 17.06857
Lesotho | -.5317529 .8723967 -0.61 0.542 -2.241823 1.178317
Liberia | 1.542089 .8724078 1.77 0.077 -.1680029 3.252181
Libya | 15.88397 .8774943 18.10 0.000 14.16391 17.60404
Lithuania | 14.66823 .8784287 16.70 0.000 12.94634 16.39012
Luxembourg | 9.029789 .9635371 9.37 0.000 7.141066 10.91851
Madagascar | 4.605051 .8723958 5.28 0.000 2.894982 6.315119
Malawi | -2.105175 .8723974 -2.41 0.016 -3.815246 -.3951033
Malaysia | 15.90489 .8753863 18.17 0.000 14.18896 17.62082
Maldives | 12.34994 .8740045 14.13 0.000 10.63671 14.06316
Mali | -1.42439 .8723954 -1.63 0.103 -3.134458 .2856777
Malta | 19.71873 .8803962 22.40 0.000 17.99298 21.44449
Marshall .. | 9.086459 .8724661 10.41 0.000 7.376253 10.79667
Mauritania | 8.30618 .872505 9.52 0.000 6.595897 10.01646
Mauritius | 15.06353 .8744272 17.23 0.000 13.34948 16.77758
Mexico | 14.88445 .8757381 17.00 0.000 13.16783 16.60107
Micronesi.. | 7.746696 .8724391 8.88 0.000 6.036543 9.456849
Moldova | 13.12574 .8735371 15.03 0.000 11.41343 14.83804
Monaco | -.756888 1.126048 -0.67 0.501 -2.964164 1.450388
Mongolia | 6.756974 .8726943 7.74 0.000 5.04632 8.467627
Montenegro | 17.93205 .8751064 20.49 0.000 16.21667 19.64743
Morocco | 12.55594 .8726274 14.39 0.000 10.84542 14.26647
Mozambique | -1.560659 .8724044 -1.79 0.074 -3.270745 .1494259
Myanmar | 4.216595 .8723971 4.83 0.000 2.506524 5.926666
Namibia | 4.618303 .873044 5.29 0.000 2.906964 6.329642
Nauru | 3.918531 .8788022 4.46 0.000 2.195904 5.641157
Nepal | 7.780663 .8724013 8.92 0.000 6.070584 9.490742
Netherlands | 16.98445 .8982199 18.91 0.000 15.22376 18.74514
New Zealand | 17.76939 .8878218 20.01 0.000 16.02909 19.5097
Nicaragua | 15.53338 .8725587 17.80 0.000 13.82299 17.24376
Niger | -2.031455 .8723976 -2.33 0.020 -3.741527 -.3213826
Nigeria | 2.404473 .8724685 2.76 0.006 .6942618 4.114684
North Korea | 13.13189 .872411 15.05 0.000 11.42179 14.84199
North Mac.. | 15.38226 .8741751 17.60 0.000 13.6687 17.09582
Norway | 16.02998 .9084795 17.64 0.000 14.24918 17.81078
Oman | 8.487606 .8831274 9.61 0.000 6.756501 10.21871
Pakistan | 7.452142 .8724537 8.54 0.000 5.74196 9.162324
Palau | 7.788918 .8778686 8.87 0.000 6.068122 9.509715
Palestine | 14.59931 .8725445 16.73 0.000 12.88895 16.30967
Panama | 19.84229 .8762318 22.65 0.000 18.12471 21.55988
Papua New.. | 8.534913 .8724431 9.78 0.000 6.824751 10.24507
Paraguay | 19.58811 .8733123 22.43 0.000 17.87624 21.29997
Peru | 16.93525 .8731454 19.40 0.000 15.22371 18.64678
Philippines | 14.07535 .8726172 16.13 0.000 12.36484 15.78585
Poland | 16.79875 .8766829 19.16 0.000 15.08028 18.51722
Portugal | 17.91763 .8813093 20.33 0.000 16.19009 19.64517
Qatar | 3.259827 .9677443 3.37 0.001 1.362857 5.156798
Romania | 15.05017 .875567 17.19 0.000 13.33388 16.76645
Russia | 11.33477 .8776998 12.91 0.000 9.614306 13.05524
Rwanda | .5265904 .8723958 0.60 0.546 -1.183478 2.236659
Samoa | 13.15495 .8725572 15.08 0.000 11.44456 14.86533
San Marino | 15.24963 .9237323 16.51 0.000 13.43893 17.06033
Sao Tome .. | 11.02277 .8724395 12.63 0.000 9.312619 12.73293
Saudi Ara.. | 8.209762 .8972483 9.15 0.000 6.450978 9.968546
Senegal | 5.790201 .8724193 6.64 0.000 4.080087 7.500316
Serbia | 15.42711 .8748122 17.63 0.000 13.7123 17.14191
Seychelles | 14.64614 .8764564 16.71 0.000 12.92811 16.36417
Sierra Le.. | -1.088042 .8723953 -1.25 0.212 -2.79811 .6220254
Singapore | 14.54489 .9131093 15.93 0.000 12.75501 16.33476
Slovak Re.. | 16.21032 .8774309 18.47 0.000 14.49038 17.93025
Slovenia | 16.93228 .8835445 19.16 0.000 15.20036 18.6642
Solomon I.. | 2.142464 .8724033 2.46 0.014 .4323806 3.852547
Somalia | -2.027417 .8723986 -2.32 0.020 -3.737491 -.3173435
South Afr.. | 3.992586 .8738808 4.57 0.000 2.279607 5.705566
South Korea | 17.20977 .8792156 19.57 0.000 15.48633 18.93321
South Sudan | 3.023818 .8723975 3.47 0.001 1.313746 4.733889
Spain | 19.64801 .8850025 22.20 0.000 17.91323 21.38279
Sri Lanka | 16.8485 .8728322 19.30 0.000 15.13757 18.55942
St. Kitts.. | 11.33994 .8767748 12.93 0.000 9.621288 13.05859
St. Lucia | 16.38027 .8736387 18.75 0.000 14.66777 18.09278
St. Vince.. | 15.29897 .8732097 17.52 0.000 13.58731 17.01063
Sudan | 7.288347 .8724512 8.35 0.000 5.57817 8.998524
Suriname | 13.53323 .8751892 15.46 0.000 11.81768 15.24877
Sweden | 18.48339 .8946342 20.66 0.000 16.72973 20.23705
Switzerland | 15.97752 .9163124 17.44 0.000 14.18137 17.77368
Syria | 15.22321 .8733157 17.43 0.000 13.51134 16.93508
Taiwan | 17.58298 .8827163 19.92 0.000 15.85268 19.31328
Tajikistan | 12.03292 .872467 13.79 0.000 10.32271 13.74313
Tanzania | 3.645635 .8723954 4.18 0.000 1.935567 5.355702
Thailand | 16.88291 .8735696 19.33 0.000 15.17054 18.59528
Timor-Leste | 8.317864 .8724089 9.53 0.000 6.607769 10.02796
Togo | 4.267778 .8723962 4.89 0.000 2.557708 5.977847
Tonga | 16.35965 .8725161 18.75 0.000 14.64935 18.06995
Trinidad .. | 13.54054 .8773561 15.43 0.000 11.82075 15.26033
Tunisia | 16.92592 .8729871 19.39 0.000 15.2147 18.63715
Turkey | 14.48794 .8758145 16.54 0.000 12.77117 16.20471
Turkmenis~n | 11.00744 .8731582 12.61 0.000 9.29588 12.71901
Tuvalu | 8.504581 .8724449 9.75 0.000 6.794416 10.21475
UAE | 1.377637 .9624561 1.43 0.152 -.5089676 3.264241
UK | 17.14749 .8904927 19.26 0.000 15.40195 18.89303
USA | 14.06179 .9045857 15.55 0.000 12.28862 15.83495
Uganda | .7819791 .8723953 0.90 0.370 -.9280885 2.492047
Ukraine | 14.4127 .8740233 16.49 0.000 12.69944 16.12596
Uruguay | 17.48096 .8754565 19.97 0.000 15.7649 19.19703
Uzbekistan | 12.32152 .8726142 14.12 0.000 10.61102 14.03202
Vanuatu | 9.043494 .8724225 10.37 0.000 7.333373 10.75361
Venezuela | 15.89228 .8760994 18.14 0.000 14.17495 17.60961
Vietnam | 15.30201 .8725267 17.54 0.000 13.59169 17.01234
Yemen | 6.324304 .8724412 7.25 0.000 4.614146 8.034461
Zambia | .0177563 .8724121 0.02 0.984 -1.692344 1.727857
Zimbabwe | 2.543638 .8724076 2.92 0.004 .8335466 4.25373
|
_cons | 53.56116 .61693 86.82 0.000 52.35185 54.77046
------------------------------------------------------------------------------Afghanistan is the first country in the data set, so the coefficients for the other countries represent the difference in life expectancy between them and Afghanistan (controlling for gdp_pcap). Most but not all are positive, and many are quite large. R-squared also increased by a lot. Clearly country is important here.
On the other hand, it sure is a lot of coefficients. If we’re just trying to get the right coefficient on gdp_pcap and we’re just controlling for country, we don’t really care about all the country coefficients. We just say we’re including country fixed effects and call it good.
The xtreg command will take care of that for us, but the data needs to be xtset so it understands the structure of the data. In particular, it needs to know the variable that identifies the countries and the variable that identifies time. Then when we tell xtreg we want fixed effects, it knows we want fixed effects for countries.
xtset cnum year
xtreg life_exp gdp_pcap, fe
Panel variable: cnum (strongly balanced)
Time variable: year, 1971 to 2023
Delta: 1 unit
Fixed-effects (within) regression Number of obs = 10,335
Group variable: cnum Number of groups = 195
R-squared: Obs per group:
Within = 0.1078 min = 53
Between = 0.3822 avg = 53.0
Overall = 0.3090 max = 53
F(1, 10139) = 1225.37
corr(u_i, Xb) = 0.2254 Prob > F = 0.0000
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
gdp_pcap | 18.86835 .5390142 35.01 0.000 17.81178 19.92493
_cons | 64.41851 .0940855 684.68 0.000 64.23408 64.60293
-------------+----------------------------------------------------------------
sigma_u | 6.6714422
sigma_e | 4.4909296
rho | .68816462 (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(194, 10139) = 111.02 Prob > F = 0.0000Stata refers to the fixed effects as u. So sigma_u tells us the standard deviation of the fixed effects, and rho tells us how much of the variance is explained by the fixed effects (a lot, because countries are very different). But it doesn’t report the actual coefficients.
Putting in a coefficient for each country turns out to be mathematically equivalent to calculating the mean value of all the variables for each country and then subtracting it from all the values for that country. Thus the model only looks at the variation over time within each country in estimating the effect of life_exp. Note that this means you can’t include any predictors that don’t change over time in a fixed effects model. The model can’t tell the difference between a variable that’s always the same for a country and the effect of the country itself.
An obvious problem with this regression is that per-capita GDP usually increases over time, and lots of other things change over time. So some of the effect we observe for gdp_pcap could actually be due to other things that change over time. So let’s include time in the model but what’s the form of the relationship? To see, graph the mean of life_exp by year.
graph bar (mean) life_exp, over(year)
Well that’s not very useful! This is why your default for bar graphs should be horizontal.
graph hbar (mean) life_exp, over(year, label(labsize(vsmall)))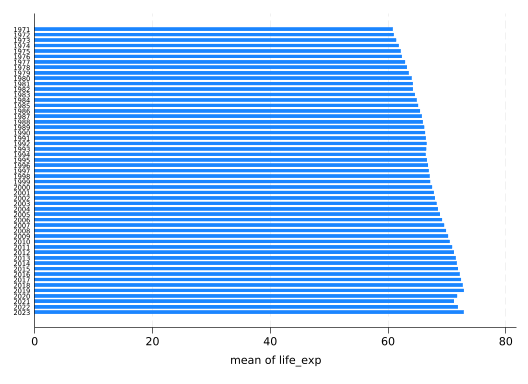
The relationship is not all that linear–and then we’ve got the COVID-19 pandemic at the end. So rather than treating year as a continuous variable and assuming a linear relationship with life_exp, let’s add fixed effects for time too. xtreg only does fixed effects for each subject automatically, but we can tell it to absorb the year variable, which essentially means put in i.year without reporting coefficients for it.
xtreg life_exp gdp_pcap, fe absorb(year)
Halperin APM for regression coefficients:
Dependent variable:
Iteration 1: Maximum absolute difference = 2.109e-13
Independent variables:
Iteration 1: Maximum absolute difference = 2.057e-14
Halperin APM for panel effects:
Iteration 1: Maximum absolute difference = 13.22
Iteration 2: Maximum absolute difference = 6.402e-15
Fixed-effects (within) regression Number of obs = 10,335
Group variable: cnum Number of groups = 195
R-squared: Obs per group:
Within = 0.5373 min = 53
Between = 0.3822 avg = 53.0
Overall = 0.3090 max = 53
F(1, 10087) = 1.87
corr(u_i, Xb) = -0.5709 Prob > F = 0.1711
--------------------------
Absorbed variable | Levels
------------------+-------
year | 53
--------------------------
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
gdp_pcap | -.6062292 .4429366 -1.37 0.171 -1.474473 .2620147
_cons | 67.41982 .0753466 894.80 0.000 67.27213 67.56752
-------------+----------------------------------------------------------------
sigma_u | 8.292725
sigma_e | 3.2424726
rho | .867391 (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(194, 10087) = 261.24 Prob > F = 0.0000After controlling for time and country gdp_pcap has no effect on life_exp. Do you believe that? Not without checking model diagnostics!
There are several different ways you can calculate the predicted values for a fixed effect model, so you can’t just use rvfplot. We want to include the fixed effects in calculating the predicted values and use the individual-level error in looking at residuals.
predict life_exp_hat, xbu
predict residual, e
Halperin APM for panel effects:
Iteration 1: Maximum absolute difference = 13.22
Iteration 2: Maximum absolute difference = 6.402e-15
Halperin APM for absorbed effects:
Iteration 1: Maximum absolute difference = 3.400e-13scatter residual life_exp_hat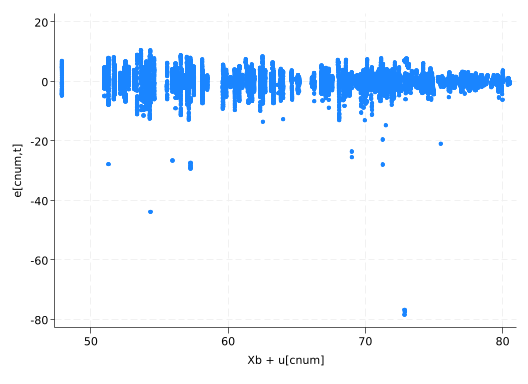
scatter residual gdp_pcap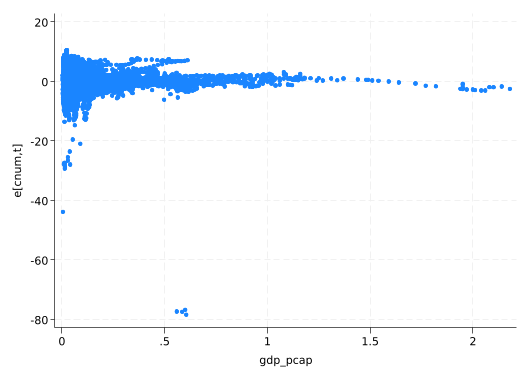
The downward trend is a bit concerning, as is the fact that there are some big negative residuals but no corresponding big positive residuals.
hist residual(bin=40, start=-78.38623, width=2.2226786)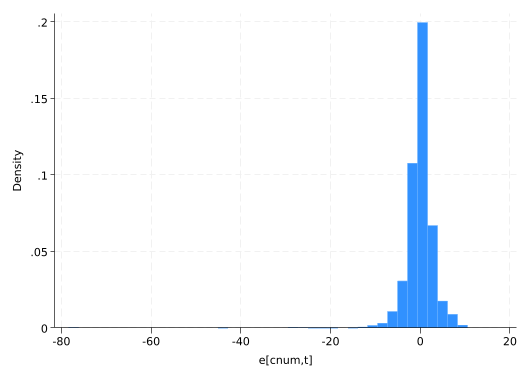
Take a closer look without the big negative residuals.
hist residual if residual>-15(bin=40, start=-14.741642, width=.63156393)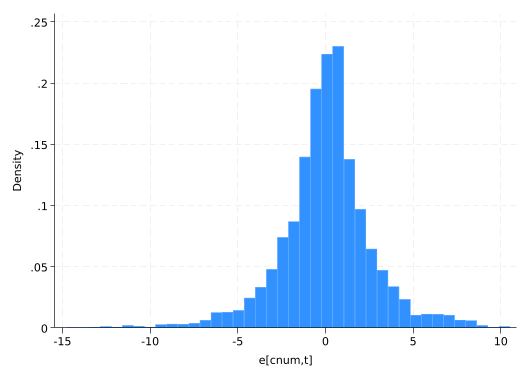
qnorm residual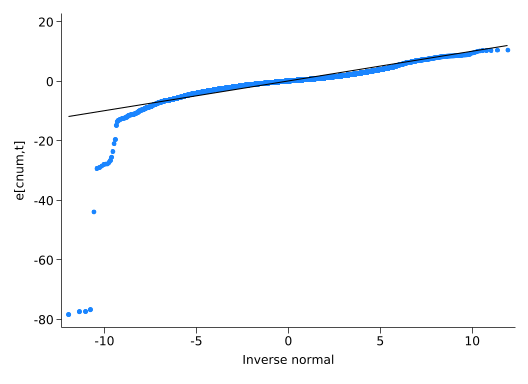
So all admirably normal, except for those big negative residuals. What’s up with those?
list country year life_exp gdp_pcap residual if residual<-15
+-----------------------------------------------------------+
| country year life_exp gdp_pcap residual |
|-----------------------------------------------------------|
1433. | Burundi 1972 17.1 .00936 -27.77646 |
1489. | Cambodia 1975 24.7 .0131 -27.31961 |
1490. | Cambodia 1976 24.5 .014 -27.74986 |
1491. | Cambodia 1977 24.4 .0138 -28.41938 |
1492. | Cambodia 1978 24.2 .0149 -28.91995 |
|-----------------------------------------------------------|
1493. | Cambodia 1979 24.1 .0142 -29.30515 |
2336. | Cyprus 1974 49 .0898 -20.94798 |
3856. | Haiti 2010 32.5 .0294 -26.58132 |
3972. | Hong Kong, China 2020 0 .559 -77.32952 |
3973. | Hong Kong, China 2021 0 .6 -76.7635 |
|-----------------------------------------------------------|
3974. | Hong Kong, China 2022 0 .585 -77.43473 |
3975. | Hong Kong, China 2023 0 .605 -78.38623 |
4988. | Lebanon 1976 38.3 .0403 -27.95316 |
4994. | Lebanon 1982 48.6 .0526 -19.52872 |
6999. | Palestine 1973 37.6 .0294 -25.46058 |
|-----------------------------------------------------------|
7008. | Palestine 1982 42.3 .0382 -23.5813 |
7603. | Rwanda 1994 9.5 .00539 -43.86348 |
+-----------------------------------------------------------+Oh…it’s civil wars, invasions, the Khmer Rouge, and the Haiti earthquake. Except for Hong Kong. Presumably once Hong Kong was returned to China they couldn’t get separate life expectancy data, but that should be missing not zero! Fix that and run the model again.
replace life_exp = . if life_exp==0(4 real changes made, 4 to missing)xtreg life_exp gdp_pcap, fe absorb(year)
Halperin APM for regression coefficients:
Dependent variable:
Iteration 1: Maximum absolute difference = .001916
Iteration 2: Maximum absolute difference = 5.736e-10
Independent variables:
Iteration 1: Maximum absolute difference = .00002363
Iteration 2: Maximum absolute difference = 2.138e-12
Halperin APM for panel effects:
Iteration 1: Maximum absolute difference = 13.02
Iteration 2: Maximum absolute difference = .4017
Iteration 3: Maximum absolute difference = .0001555
Iteration 4: Maximum absolute difference = 6.017e-08
Iteration 5: Maximum absolute difference = 2.329e-11
Fixed-effects (within) regression Number of obs = 10,331
Group variable: cnum Number of groups = 195
R-squared: Obs per group:
Within = 0.6125 min = 49
Between = 0.3839 avg = 53.0
Overall = 0.3226 max = 53
F(1, 10083) = 1.25
corr(u_i, Xb) = 0.5593 Prob > F = 0.2634
--------------------------
Absorbed variable | Levels
------------------+-------
year | 53
--------------------------
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
gdp_pcap | .4305647 .3849346 1.12 0.263 -.3239838 1.185113
_cons | 67.28618 .0654109 1028.67 0.000 67.15796 67.4144
-------------+----------------------------------------------------------------
sigma_u | 8.2109465
sigma_e | 2.8147619
rho | .8948418 (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(194, 10083) = 347.50 Prob > F = 0.0000That changed the sign, but the effect is still insignificant.
You may recall that the original example in The Effect uses the log of per-capita GDP. The curvature of the log function adds some diminishing returns to the model, which makes sense intuitively. So we’ll try that and see what we think is the better model. But before we do, let’s get the AIC and BIC for this model.
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | N ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 10,331 -30121.55 -25224.86 2 50453.73 50468.21
-----------------------------------------------------------------------------
Note: BIC uses N = number of observations. See [R] IC note.gen log_gdp_pcap = log(gdp_pcap)Start by looking at a scatterplot again.
scatter life_exp log_gdp_pcap if cnum<=10, colorvar(cnum) colordiscrete coloruseplegend zlabel(, valuelabel)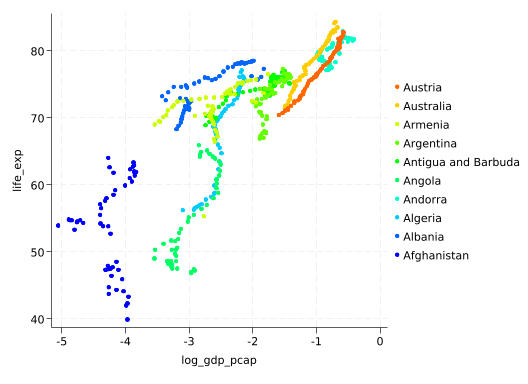
The relationship between life_exp and log_gdp_pcap does seems a little more consistent between countries, but that’s not much of a check.
xtreg life_exp log_gdp_pcap, fe absorb(year)
Halperin APM for regression coefficients:
Dependent variable:
Iteration 1: Maximum absolute difference = .001916
Iteration 2: Maximum absolute difference = 5.736e-10
Independent variables:
Iteration 1: Maximum absolute difference = .0001471
Iteration 2: Maximum absolute difference = 3.214e-12
Halperin APM for panel effects:
Iteration 1: Maximum absolute difference = 10.4
Iteration 2: Maximum absolute difference = .3452
Iteration 3: Maximum absolute difference = .0001336
Iteration 4: Maximum absolute difference = 5.172e-08
Iteration 5: Maximum absolute difference = 2.002e-11
Fixed-effects (within) regression Number of obs = 10,331
Group variable: cnum Number of groups = 195
R-squared: Obs per group:
Within = 0.6289 min = 49
Between = 0.7367 avg = 53.0
Overall = 0.6470 max = 53
F(1, 10083) = 447.11
corr(u_i, Xb) = 0.7154 Prob > F = 0.0000
--------------------------
Absorbed variable | Levels
------------------+-------
year | 53
--------------------------
------------------------------------------------------------------------------
life_exp | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
log_gdp_pcap | 1.931591 .0913496 21.15 0.000 1.752527 2.110654
_cons | 72.26024 .2336777 309.23 0.000 71.80219 72.7183
-------------+----------------------------------------------------------------
sigma_u | 6.4687092
sigma_e | 2.7545267
rho | .84650679 (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(194, 10083) = 165.41 Prob > F = 0.0000Now we’ve got a strong effect for log_gdp_pcap. But we still won’t believe it without diagnostics.
predict life_exp_hat2, xbu
predict residual2, e
Halperin APM for panel effects:
Iteration 1: Maximum absolute difference = 10.4
Iteration 2: Maximum absolute difference = .3452
Iteration 3: Maximum absolute difference = .0001336
Iteration 4: Maximum absolute difference = 5.172e-08
Iteration 5: Maximum absolute difference = 2.002e-11
(4 missing values generated)
Halperin APM for absorbed effects:
Iteration 1: Maximum absolute difference = .00178
Iteration 2: Maximum absolute difference = 7.055e-11
(4 missing values generated)scatter residual2 life_exp_hat2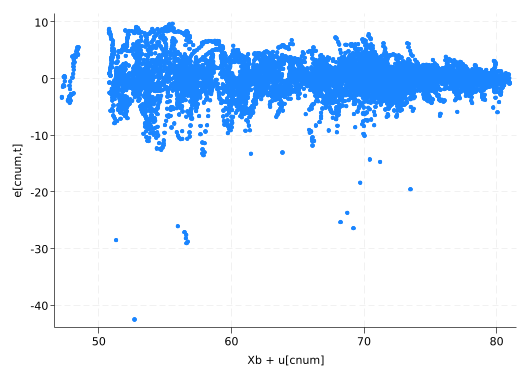
scatter residual2 log_gdp_pcap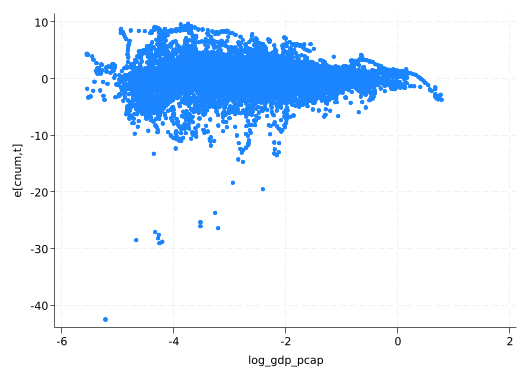
There’s somewhat less of a trend, except at the very far right end, so that’s good.
hist residual2(bin=40, start=-42.537064, width=1.3056776)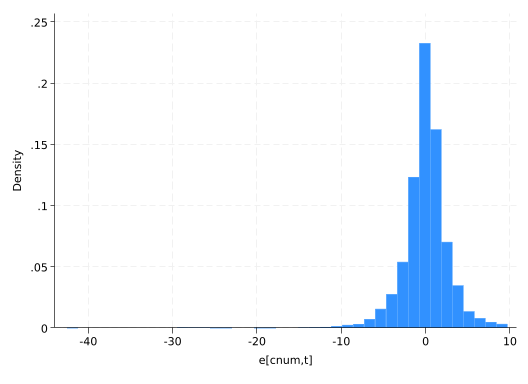
hist residual2 if residual2>-15(bin=40, start=-14.727797, width=.61044588)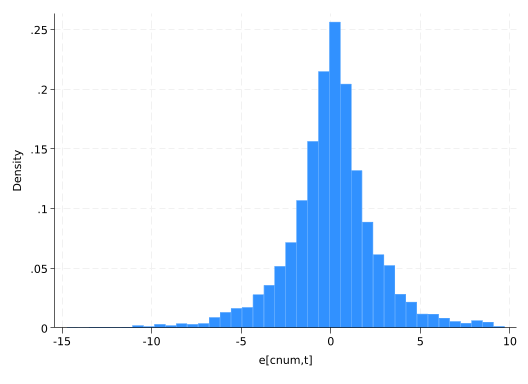
These graphs don’t make it easy to choose, so how about the information criteria?
estat ic
Akaike's information criterion and Bayesian information criterion
-----------------------------------------------------------------------------
Model | N ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
. | 10,331 -30121.55 -25001.38 2 50006.76 50021.25
-----------------------------------------------------------------------------
Note: BIC uses N = number of observations. See [R] IC note.It’s not a big difference, but both AIC and BIC are lower for the model with log_gdp_pcap, suggesting that’s the better model.