6 Mediation
6.1 Intro
The idea of mediation is that one variable (an independent variable) may influence another variable (a response) through it’s influence on a third variable (the mediator). In the following diagram, \(x\) is the independent variable, \(z\) is the response variable, and \(m\) is a mediating variable.
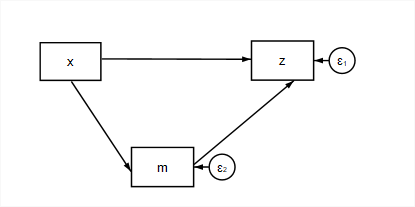
When all of the relations (direct effects) in our model are linear regressions, in addition to the coefficients that characterize
\[z = \beta_0 + \beta_1 x + \beta_2 m + \epsilon_z\] \[ m = \beta_4 + \beta_5 x + \epsilon_m\]
we are often interested in estimating the indirect effect of x on z, \(\beta_2 \beta_5\), the total effect of x on z, \((\beta_2 \beta_5) + \beta_1\), and the proportion of the total effect that is mediated by m, \(\frac{\beta_2 \beta_5}{(\beta_2 \beta_5) + \beta_1}\).
6.2 Estimation
The underlying model can be conveniently estimated through structural equations modeling. Using MPlus, not only can the software estimate the underlying model but it can also be used to give us estimates of the indirect effects, total effects, and the proportion mediated.
6.2.1 Model Indirect
The underlying model is composed of two regressions. If we add a MODEL INDIRECT command, and specify the relation between x and z as ind, this will give us the underlying coefficients, direct, indirect, and total effects.
MODEL:
z on x m;
m on x;
MODEL INDIRECT:
z ind x;yields the usual model results like
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Z ON
X 1.922 0.286 6.731 0.000
M 0.013 0.071 0.176 0.860
M ON
X 3.977 0.037 107.459 0.000
Means
X 0.075 0.070 1.083 0.279
Intercepts
M 0.047 0.037 1.300 0.193
Z -0.003 0.037 -0.083 0.934
Variances
X 0.968 0.097 10.000 0.000
Residual Variances
M 0.265 0.027 10.000 0.000
Z 0.269 0.027 10.000 0.000as well as the additional effects
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from X to Z
Total 1.972 0.037 52.919 0.000
Total indirect 0.050 0.283 0.176 0.860
Specific indirect 1
Z
M
X 0.050 0.283 0.176 0.860
Direct
Z
X 1.922 0.286 6.731 0.000In this particular example, there are no measurable indirect effects, because there is no direct effect of m on z!
6.2.2 Model Constraint
It is also possible to estimate indirect and total effects by writing our own “model constraints” (a misnomer in this case, because nothing is actually constrained). The advantage in writing your own constraints is that there is usually less output to wade through, and you can also estimate the proportion of mediation.
To achieve this, we need to label our regression coefficients in the original model command.
MODEL:
z on x (zx);
z on m (zm);
m on x (mx);
MODEL CONSTRAINT:
NEW(zmx TOTAL prop); ! declare additional variables;
zmx = zm*mx; ! Indirect effect of x on z via M;
TOTAL = zm*mx + zx; ! Total effect of X on Y;
prop = zmx/(TOTAL);In addition to the model results like before, at the end of the MODEL RESULTS section we also get
New/Additional Parameters
ZMX 0.050 0.283 0.176 0.860
TOTAL 1.972 0.037 52.919 0.000
PROP 0.025 0.144 0.176 0.8606.3 Categorical Mediators
We can certainly use categorical variables as mediators, and MPlus will estimate models with CATEGORICAL, NOMINAL, and COUNT mediators. However, because these are non-linear models, calculating and interpreting the indirect effects becomes much more complicated. The MODEL INDIRECT section is not available.