Confirmatory Factor Analysis
Suppose we want to estimate this model:
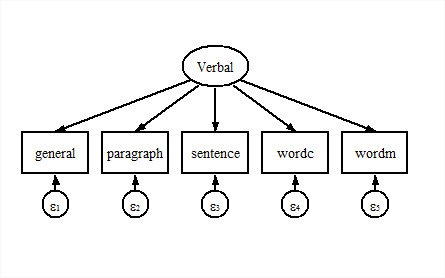
CFA
use "U:\Stata\Stata SEM\hsdata.dta"
sem (Verbal -> general paragraph sentence wordc wordm)Endogenous variables
Measurement: general paragraph sentence wordc wordm
Exogenous variables
Latent: Verbal
Fitting target model:
Iteration 0: log likelihood = -4403.8152
Iteration 1: log likelihood = -4403.4283
Iteration 2: log likelihood = -4403.4268
Iteration 3: log likelihood = -4403.4268
Structural equation model Number of obs = 301
Estimation method = ml
Log likelihood = -4403.4268
( 1) [general]Verbal = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Measurement |
general <- |
Verbal | 1 (constrained)
_cons | 40.59136 .712427 56.98 0.000 39.19503 41.98769
-----------+----------------------------------------------------------------
parag~h <- |
Verbal | .2754032 .0165074 16.68 0.000 .2430493 .3077571
_cons | 9.182724 .200961 45.69 0.000 8.788848 9.576601
-----------+----------------------------------------------------------------
sente~e <- |
Verbal | .4349704 .02364 18.40 0.000 .3886368 .4813039
_cons | 17.36213 .2970317 58.45 0.000 16.77995 17.9443
-----------+----------------------------------------------------------------
wordc <- |
Verbal | .403284 .0277438 14.54 0.000 .3489072 .4576608
_cons | 26.12625 .3265834 80.00 0.000 25.48615 26.76634
-----------+----------------------------------------------------------------
wordm <- |
Verbal | .6238506 .0348107 17.92 0.000 .5556229 .6920784
_cons | 15.299 .4413117 34.67 0.000 14.43405 16.16396
-------------+----------------------------------------------------------------
var(e.gene~l)| 45.59075 4.800626 37.08914 56.04112
var(e.para~h)| 4.026519 .4034455 3.308582 4.900244
var(e.sent~e)| 6.277734 .7412008 4.980845 7.9123
var(e.wordc)| 14.67172 1.3443 12.25997 17.5579
var(e.wordm)| 16.90726 1.805241 13.71475 20.84293
var(Verbal)| 107.1825 12.26806 85.64373 134.138
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(5) = 18.74, Prob > chi2 = 0.0021Note that Verbal is a latent variable, it does not appear in our data set. The capitalization here is important - it tells Stata that this is a latent variable, and not some kind of mistake!
Without capitalization, Stata thinks verbal is just a variable that is somehow missing from the data, a mistake.
sem (verbal -> general paragraph sentence wordc wordm)Perhaps you meant 'verbal' to specify a latent variable.
For 'verbal' to be a valid latent variable specification, 'verbal' must begin
with a capital letter.
r(111);
end of do-file
r(111);Ordinarily, Stata will assume that variable names that begin with capitalization represent latent variables, while lower-case names represent variables that should be in our data set. If there are manifest variables with capitalized names, we can turn off this interpretation with a nocapslatent option. If we do this, then any latent variable will have to be declared with a latent() option, and this is also how we can have uncapitalized latent variable names.
sem (verbal -> general paragraph sentence wordc wordm), latent(verbal)Endogenous variables
Measurement: general paragraph sentence wordc wordm
Exogenous variables
Latent: verbal
Fitting target model:
Iteration 0: log likelihood = -4403.8152
Iteration 1: log likelihood = -4403.4283
Iteration 2: log likelihood = -4403.4268
Iteration 3: log likelihood = -4403.4268
Structural equation model Number of obs = 301
Estimation method = ml
Log likelihood = -4403.4268
( 1) [general]verbal = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Measurement |
general <- |
verbal | 1 (constrained)
_cons | 40.59136 .712427 56.98 0.000 39.19503 41.98769
-----------+----------------------------------------------------------------
parag~h <- |
verbal | .2754032 .0165074 16.68 0.000 .2430493 .3077571
_cons | 9.182724 .200961 45.69 0.000 8.788848 9.576601
-----------+----------------------------------------------------------------
sente~e <- |
verbal | .4349704 .02364 18.40 0.000 .3886368 .4813039
_cons | 17.36213 .2970317 58.45 0.000 16.77995 17.9443
-----------+----------------------------------------------------------------
wordc <- |
verbal | .403284 .0277438 14.54 0.000 .3489072 .4576608
_cons | 26.12625 .3265834 80.00 0.000 25.48615 26.76634
-----------+----------------------------------------------------------------
wordm <- |
verbal | .6238506 .0348107 17.92 0.000 .5556229 .6920784
_cons | 15.299 .4413117 34.67 0.000 14.43405 16.16396
-------------+----------------------------------------------------------------
var(e.gene~l)| 45.59075 4.800626 37.08914 56.04112
var(e.para~h)| 4.026519 .4034455 3.308582 4.900244
var(e.sent~e)| 6.277734 .7412008 4.980845 7.9123
var(e.wordc)| 14.67172 1.3443 12.25997 17.5579
var(e.wordm)| 16.90726 1.805241 13.71475 20.84293
var(verbal)| 107.1825 12.26806 85.64373 134.138
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(5) = 18.74, Prob > chi2 = 0.0021Identifying Constraints
sem (Verbal -> general paragraph@1 sentence wordc wordm)Endogenous variables
Measurement: general paragraph sentence wordc wordm
Exogenous variables
Latent: Verbal
Fitting target model:
Iteration 0: log likelihood = -4403.883
Iteration 1: log likelihood = -4403.4276
Iteration 2: log likelihood = -4403.4268
Iteration 3: log likelihood = -4403.4268
Structural equation model Number of obs = 301
Estimation method = ml
Log likelihood = -4403.4268
( 1) [paragraph]Verbal = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Measurement |
general <- |
Verbal | 3.63104 .2176409 16.68 0.000 3.204471 4.057608
_cons | 40.59136 .712427 56.98 0.000 39.19503 41.98769
-----------+----------------------------------------------------------------
parag~h <- |
Verbal | 1 (constrained)
_cons | 9.182724 .200961 45.69 0.000 8.788848 9.576601
-----------+----------------------------------------------------------------
sente~e <- |
Verbal | 1.579395 .087443 18.06 0.000 1.40801 1.75078
_cons | 17.36213 .2970317 58.45 0.000 16.77995 17.9443
-----------+----------------------------------------------------------------
wordc <- |
Verbal | 1.46434 .1040185 14.08 0.000 1.260468 1.668213
_cons | 26.12625 .3265834 80.00 0.000 25.48615 26.76634
-----------+----------------------------------------------------------------
wordm <- |
Verbal | 2.265226 .1325247 17.09 0.000 2.005483 2.52497
_cons | 15.299 .4413117 34.67 0.000 14.43405 16.16396
-------------+----------------------------------------------------------------
var(e.gene~l)| 45.59075 4.800626 37.08914 56.04112
var(e.para~h)| 4.026519 .4034455 3.308582 4.900244
var(e.sent~e)| 6.277734 .7412008 4.980845 7.9123
var(e.wordc)| 14.67172 1.3443 12.25997 17.5579
var(e.wordm)| 16.90726 1.805241 13.71475 20.84293
var(Verbal)| 8.129461 .9639301 6.443661 10.2563
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(5) = 18.74, Prob > chi2 = 0.0021sem (Verbal -> general paragraph sentence wordc wordm), var(Verbal@1)Endogenous variables
Measurement: general paragraph sentence wordc wordm
Exogenous variables
Latent: Verbal
Fitting target model:
Iteration 0: log likelihood = -4403.8152
Iteration 1: log likelihood = -4403.4287
Iteration 2: log likelihood = -4403.4268
Iteration 3: log likelihood = -4403.4268
Structural equation model Number of obs = 301
Estimation method = ml
Log likelihood = -4403.4268
( 1) [var(Verbal)]_cons = 1
------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
Measurement |
general <- |
Verbal | 10.3529 .5924941 17.47 0.000 9.191629 11.51416
_cons | 40.59136 .712427 56.98 0.000 39.19503 41.98769
-----------+----------------------------------------------------------------
parag~h <- |
Verbal | 2.851221 .1690381 16.87 0.000 2.519912 3.18253
_cons | 9.182724 .200961 45.69 0.000 8.788848 9.576601
-----------+----------------------------------------------------------------
sente~e <- |
Verbal | 4.503203 .2410116 18.68 0.000 4.030829 4.975577
_cons | 17.36213 .2970317 58.45 0.000 16.77995 17.9443
-----------+----------------------------------------------------------------
wordc <- |
Verbal | 4.175158 .2882786 14.48 0.000 3.610142 4.740173
_cons | 26.12625 .3265834 80.00 0.000 25.48615 26.76634
-----------+----------------------------------------------------------------
wordm <- |
Verbal | 6.458661 .3655284 17.67 0.000 5.742238 7.175083
_cons | 15.299 .4413117 34.67 0.000 14.43405 16.16396
-------------+----------------------------------------------------------------
var(e.gene~l)| 45.59075 4.800626 37.08914 56.04112
var(e.para~h)| 4.026519 .4034455 3.308582 4.900244
var(e.sent~e)| 6.277734 .7412008 4.980845 7.9123
var(e.wordc)| 14.67172 1.3443 12.25997 17.5579
var(e.wordm)| 16.90726 1.805241 13.71475 20.84293
var(Verbal)| 1 (constrained)
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(5) = 18.74, Prob > chi2 = 0.0021