Proc Steps
With the data in SAS format, we can use various statistical PROCs to graph and analyze the data.
Sgplot
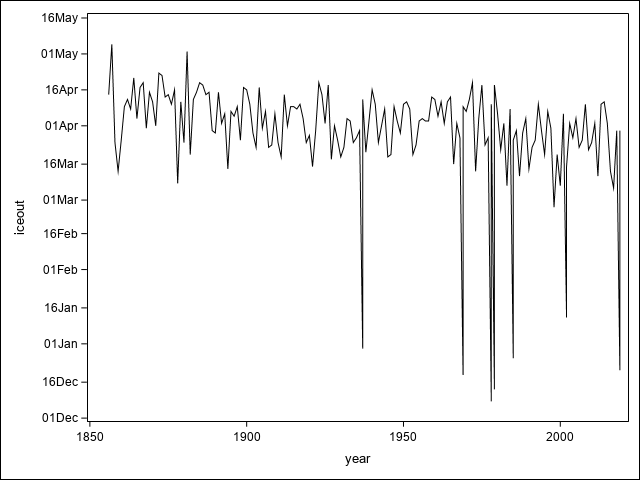
proc sgplot data=MendotaIce;
series y=iceout x=year;
yaxis tickvalueformat= data;
run;There are seven suspiciously early ice out dates, which should make us look more closely at the data.
Obs Winter Days year close open icein dur iceout
85 1936-37 . 1937 12/07/1936 12/30/1936 07DEC 23 30DEC
86 1936-37 121 1937 01/05/1937 04/13/1937 05JAN 98 12APR In some winters the lake freezes over, opens a little, then refreezes. Let's agree that we are interested in the ultimate ice out date, so we want to drop a few observations in our analysis.
Means
A simple answer to our question can be found with PROC MEANS.
proc means data=MendotaIce; * simple descriptives;
where iceout gt "12Jan60"d;
var iceout;
run; The MEANS Procedure
Analysis Variable : iceout
N Mean Std Dev Minimum Maximum
-------------------------------------------------------------------
164 92.3414634 11.6768551 57.0000000 125.0000000
-------------------------------------------------------------------Over the last 150+ years, the ice usually breaks up around the 92nd or 93rd day of the year.
We could apply our date format to interpret these results more easily.
iceout
02APR The hefty standard deviation tells us we have to allow a large margin of error in guessing an ice out date.
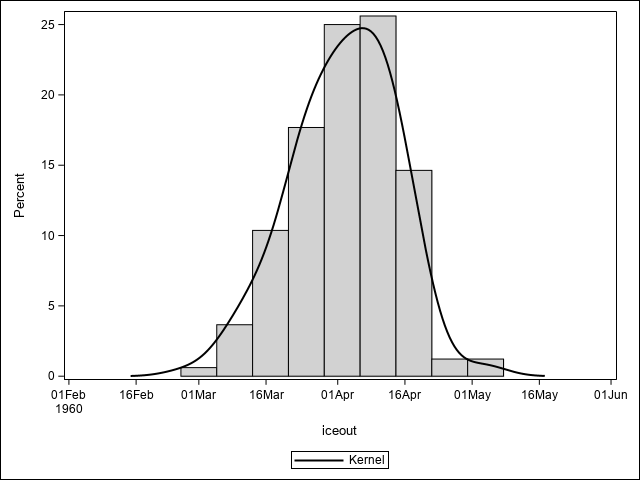
To see the distribution of the ice out date, we can use a PROC step that produces graphs.
proc sgplot data=MendotaIce;
where iceout gt "12Jan60"d;
histogram iceout;
density iceout /type=kernel;
run;Freq
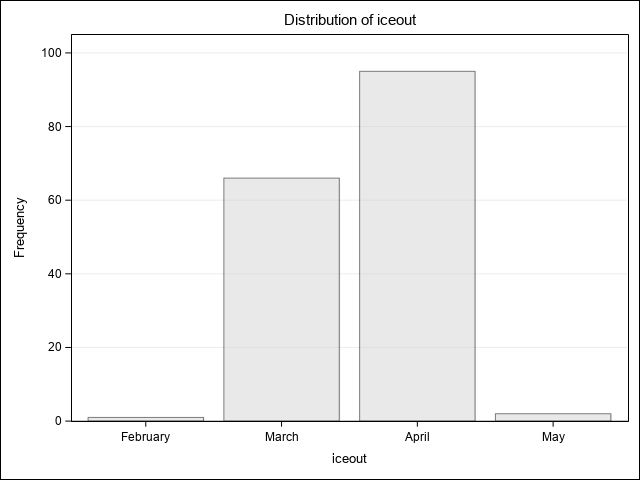
Many procedures produce both tables and plots. To look at the distribution of ice out by month we could do this:
proc freq data=MendotaIce;
where iceout gt "12Jan60"d;
tables iceout / plots=freqplot;
format iceout monname.;
run;Reg
Can we do better if we take global warming into account?
proc reg data=MendotaIce;
where iceout gt "12Jan60"d;
model iceout = year;
run; quit;
| Number of Observations Read | 164 |
|---|---|
| Number of Observations Used | 164 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF |
Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 1 | 2961.12546 | 2961.12546 | 24.90 | <.0001 |
| Error | 162 | 19264 | 118.91205 | ||
| Corrected Total | 163 | 22225 | |||
| Root MSE | 10.90468 | R-Square | 0.1332 |
|---|---|---|---|
| Dependent Mean | 92.34146 | Adj R-Sq | 0.1279 |
| Coeff Var | 11.80908 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF |
Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 266.24285 | 34.85918 | 7.64 | <.0001 |
| year | 1 | -0.08976 | 0.01799 | -4.99 | <.0001 |
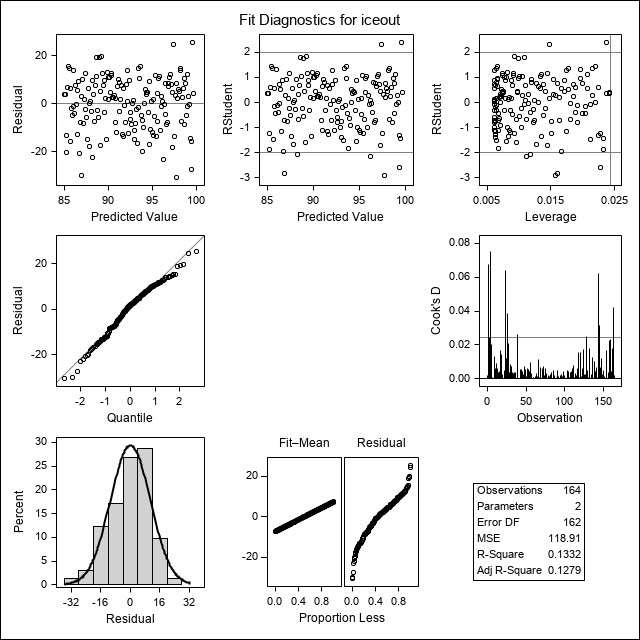
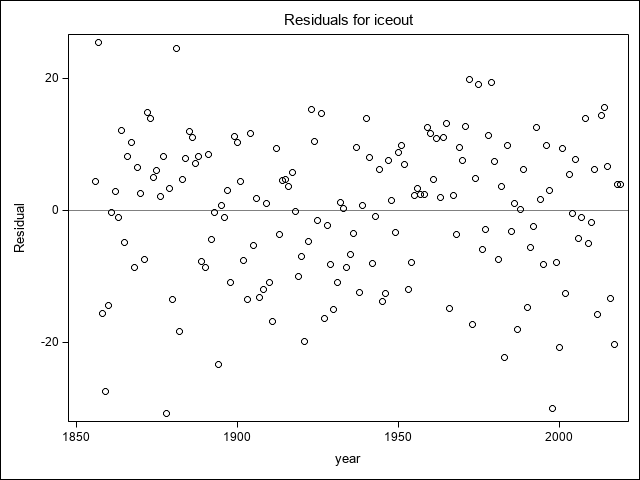
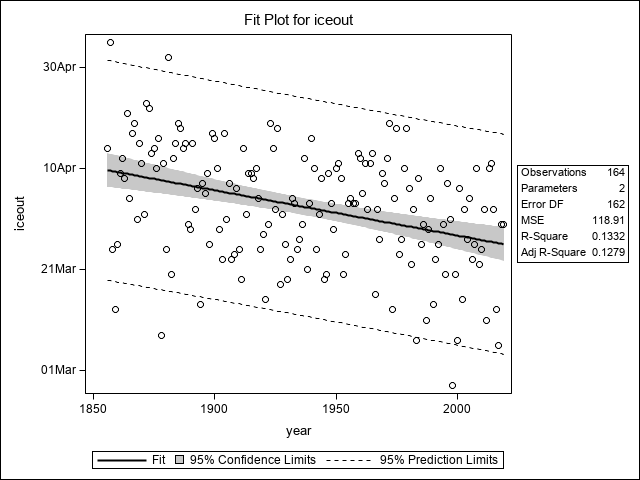
What does the intercept, about 270, mean?
Estimate
23SEP While mathematically correct, and usable to calculate a prediction for 2020, it might make sense to rescale year to simply give us our answer.
data recentered;
set mendotaice;
yearc = year-2020;
run;Notice that the intercept changes but the slope does not.
proc reg data=recentered plots=none;
where iceout gt "12Jan60"d;
model iceout = yearc;
run; quit;
| Number of Observations Read | 164 |
|---|---|
| Number of Observations Used | 164 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF |
Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 1 | 2961.12546 | 2961.12546 | 24.90 | <.0001 |
| Error | 162 | 19264 | 118.91205 | ||
| Corrected Total | 163 | 22225 | |||
| Root MSE | 10.90468 | R-Square | 0.1332 |
|---|---|---|---|
| Dependent Mean | 92.34146 | Adj R-Sq | 0.1279 |
| Coeff Var | 11.80908 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF |
Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 84.93663 | 1.71084 | 49.65 | <.0001 |
| yearc | 1 | -0.08976 | 0.01799 | -4.99 | <.0001 |
Now the intercept means the expected ice out date for this year:
Estimate
25MAR About a week earlier than if we ignore the trend.
Over the course of a lifetime, ice fishing season had ended about a week earlier, and winter is about two weeks shorter.